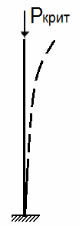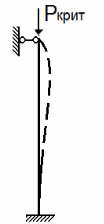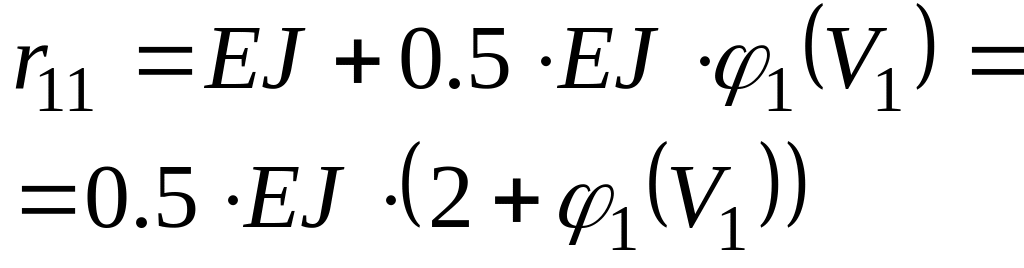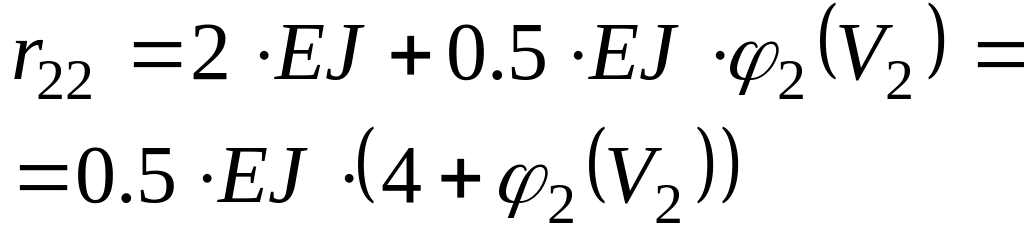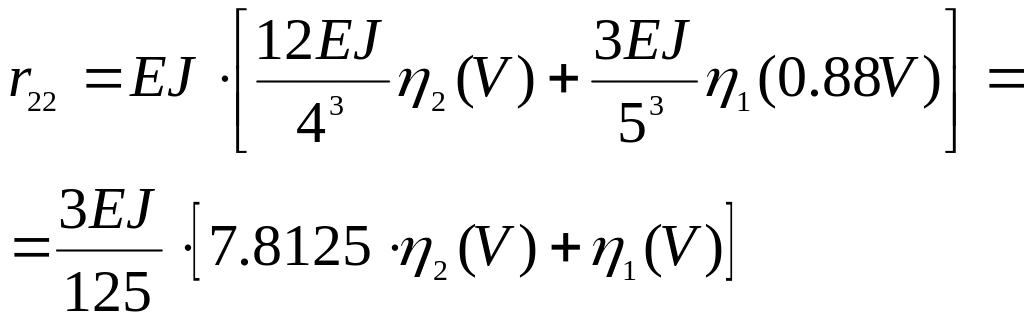Лекция №3 Расчёт плоской рамы на устойчивость

Устойчивостью называется способность сооружения сохранять своё первоначальное положение или первоначальную форму равновесия в деформированном состоянии при действии внешних сил.

В соответствии с этим необходимо различать устойчивость положения сооружения и устойчивость форм равновесия в нагруженном состоянии.

Положение сооружения или форма равновесия в нагруженном состоянии считается устойчивым, если при всяком, сколь угодно малом дополнительном возмущении, сооружение отклоняется от исследуемого положения или равновесного состояния, однако после исчезновения дополнительного возмущения полностью возвращается в исходное состояние (для упругих систем) или проявляет тенденцию к возвращению в исходное состояние (для упругопластических систем).

Положение сооружения или форма равновесия в нагруженном состоянии считается неустойчивым, если при каком-либо сколь угодно малом отклонении от исследуемого равновесного состояния и после исчезновения возмущения сооружение не проявляет тенденции к уменьшению получаемых отклонений, а иногда отклоняется ещё далее- до нового положения или новой формы равновесного состояния.

Переход сооружения из одного равновесного состояния к другому равновесному состоянию называется потерей устойчивости системы. Состояние перехода называется критическим состоянием. При этом величины внешних сил, действующие на сооружение, называются критическими.

Устойчивое и неустойчивое равновесие:

Так как конструкции, как правило надёжно закреплены, то более важной является потеря устойчивости, связанная со сменой формы деформированного состояния, которую называют потерей устойчивости первого рода, что свойственно только упругим системам. При этом наибольшее практическое значение имеет определение критических значений внешних сил. Опасность потери устойчивости особенно велика для тонкостенных конструкций, стержней, пластинок и оболочек.

В сопротивлении материалов была решена задача Эйлера о потере устойчивости прямолинейного стержня. Применяя метод сечений, убеждаемся, что в результате искривления оси в поперечных сечениях стержня возникают два внутренних силовых фактора- продольная сила и изгибающий момент . Таким образом стержень испытывает сочетание деформаций центрального сжатия и изгиба.

Установлено, что величина сжимающей силы равна:

, где -целое число ,но для практических расчётов, как правило определяется критическое значение внешней силы, соответствующее низшей форме потери устойчивости системы, т.е. .

Чтобы можно было использовать полученную формулу для различно прикреплённых стержней было введено понятие приведенной длины , где -коэффициент приведения.

Для наиболее часто встречающихся способах закрепления концов стержня приведём значения: оба конца стержня закреплены шарнирно и могут сближаться (Рисунок б), нижний конец жёстко защемлён , верхний свободен (Рисунок а), оба конца жёстко защемлены, но могут сближаться (Рисунок в), нижний конец жёстко защемлён, а верхний шарнирно, концы могут сближаться (Рисунок г) .Заметим, чем меньше , тем больше критическая сила. Например, сжимающая нагрузка стержня, жестко защемлённого обоими концами, может быть в 16 раз больше нагрузки стержня, защемлённого одним концом.

Таким образом, наименьшее значение критической силы определяем по формуле , где - приведённая длина стержня.

При анализе потери устойчивости рамных конструкций воспользоваться данной таблицей впрямую нет возможности, так как стержни в раме скреплены между собой, поэтому для определения критических сил используем метод перемещений в канонической форме, разработанный А. Ф. Смирновым.

Предположим, что все элементы заданной системы изначально имеют прямолинейную форму и сопряжены между собой под прямым углом. В данном случае при действии узловых нагрузок начальная форма равновесного состояния системы соответствует докритической стадии работы конструкций, в поперечных сечениях элементов возникают только продольные силы, и стержни работают либо на сжатие, либо на растяжение.

Считаем, что рама дважды кинематически неопределима и для нее, канонические уравнения метода перемещений записываются в форме:

(3.1)

Так как в новом равновесном (критическом) состоянии, составные элементы искривляются, то все заведомо не могут быть равны нулю. А единичные реакции , как при расчёте обычных статических задач, определяются из условия равновесия узлов или отдельных частей основной системы при заданных единичных смещениях. Система уравнений (3.1) является однородной, необходимо найти и , что возможно только при условии линейной зависимости уравнений. Математически это означает, что определитель составленный из коэффициентов равен нулю:

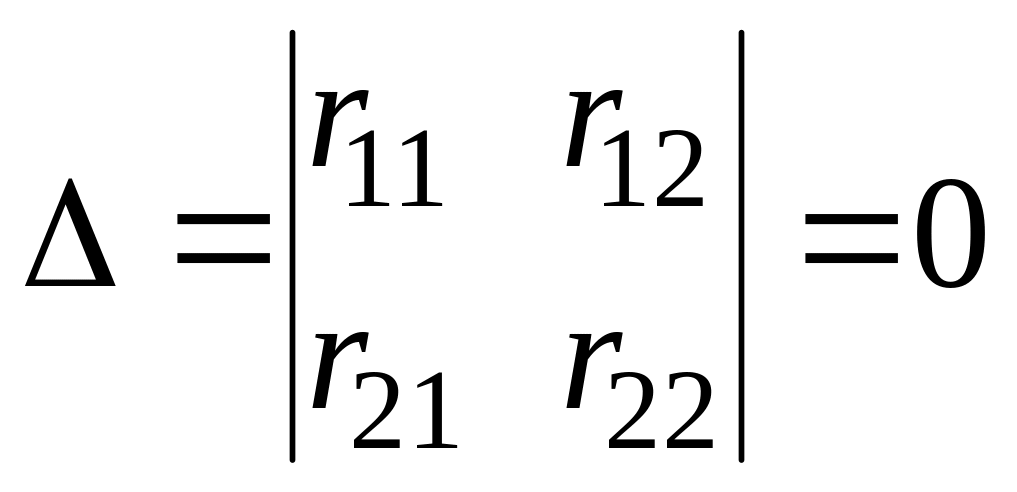(3.2)

Он носит название определитель устойчивости.

Раскрыв определитель и приравняв его к нулю, получим трансцендентное уравнение относительно параметра критической нагрузки .

Решив это уравнение относительно и по минимальному значению корня определяют критическое значение внешних сил с помощью модифицированной формулы Эйлера:

, (3.3)

где параметр учитывает различные виды закрепления стержней.

Рисунок 3.1

_{При анализе классической формулы Эйлера и полученной модифицированной видно, что параметр} .

_{Далее рассмотрим примеры расчёта рам методом перемещений.}

_{Пример № 3.1}

Рисунок 3.2

Дано: , схема рамы на Рисунке 3.2. Найти значение критической силы Решение: Выберем основную систему метода перемещений , а стержни вдоль которых приложены силы пронумеруем.

Т.к. силы приложены вдоль стержней, то грузовая эпюра будет нулевой, а соответствующие ей грузовые слагаемые: . Построим единичные эпюры. Стержни 1 и 2 являются сжато изогнутыми и эпюры на них строятся по специальным таблицам для расчёта на устойчивость методом перемещений (таблица №4 Приложения). Они носят криволинейных характер и ординаты зависят от параметра влияния продольных сил. В остальных стержнях по таблице №3 Приложения.

Основная система: Рисунок 3.3

Каноническая система метода перемещений: (3.1) Система уравнений (3.1) является однородной, необходимо найти и , что возможно только при условии линейной зависимости уравнений. Математически это означает, что определитель составленный из коэффициентов равен нулю.

или

(3.2)

для более сложных рам определитель будет более высокого порядка.

Рисунок 3.4	Строим единичные эпюры от в основной системе (Рисунок 3.3) получаем схему Рисунка 3.4. Значения функций определяется численно методом подбора по таблице №5 Приложения.
Рисунок 3.5	Единичная эпюра от (Рисунок 3.5), построенная в основной системе (Рисунок 3.3).

Значение коэффициентов определителя найдем путём вырезания узлов, как в обычном методе перемещений. Данные для коэффициентов берём из Рисунков 3.4 и 3.5, методом вырезания узлов.

Подставим полученные коэффициенты в определитель (3.2) и вынесем общий множитель 0,5 EJ, тогда

, (3.4)

выразим параметры и через общий параметр , тогда учитывая, что , то для заданных стержней:

,

за единицу измерения примем стержень №2, тогда .

Равенство (3.4) примет вид:

Решим его численно методом подбора, занося данные в таблицу:

	0,53
5,8	3,1	0,0424	-2,7777	1,496
5,9	3,13	0,0424	-3,6878	-0,362

Так как искомое решение находится между полученными значениями, а промежуточных параметров V в таблице функций нет, решение необходимо уточнить. Воспользуемся графической интерпретацией.

Из подобия треугольников: , значение параметра:

Найдём значение критической силы по формуле Эйлера: (в формулу подставляем длину того стержня, который брали за единицу измерения)

.

Пример №3.2

Рисунок 3.6

Дано: Для схемы Рисунка 3.6 ,

Найти значение критической силы.

Решаем задачу методом перемещений

Основная система Рисунок 3.7

Стержни, вдоль которых приложены силы, будут иметь криволинейные эпюры. А т.к. эти силы разные, то необходимо стержни пронумеровать.

Выразим параметры стержней друг через друга

, то

Обозначим , тогда

Найдём коэффициенты определителя, построив единичные эпюры в основной системе (Рисунок 3.7) от и по таблицам № 3,4 Приложения и методом вырезания узла и ригеля определим коэффициенты определителя устойчивости (3.2).

Тогда определитель устойчивости (3.2) примет вид:

Чтобы упростить равенство, умножим его на

Решим полученное уравнение численно, методом подбора (как в предыдущей задаче):

5	4,4	-0,4772	-1,6040	-21,781	0,4793	-2,128
5,1	4,5	-0,6100	-1,7155	22,105	0,4520	-2,154
3	2,64	0,6560	0,0893	-1,9473	0,8393	-5,572
2,5	2,2	0,7720	0,3701	-0,9931	0,8909	-2,236
2,2	1,94	0,8237	0,5131	-0,5542	0,9164	-0,348
2	1,76	0,8590	0,5980	-0,2457	0,9313	0,933
2,1	1,85	0,8437	0,5565	-0,3951	0,9240	0,308
2,15	1,9	0,8356	0,5351	-0,4736	0,9203	-0,0117

Как видно из расчёта, функции входящие в равенство не линейные, например сравните значения при и они практически одинаковы. Однако значение определителя при выпадает из этого диапазона, поэтому по двум далеко отстоящим значениям параметра интерполировать решение нельзя.

Значение критической силы найдем по формуле Эйлера: