Real
.doc|
1.Основные понятия и определения. Машина, устройство, агрегат производственный процесс называются автоматическими, если они выполняют свои функции самостоятельно без вмешательства человека. Агрегат, в котором протекает процесс подлежащий регулированию наз-ся регулируемым объектом. Величина, которую необходимо поддерживать постоянной или изменять п заданному закону наз-ся регулируемой величиной. Автоматически действующее устройство предназначенное для выполнения задачи регулирования наз-ся автоматическим регулятором. В частном случае регулятором может являться ЭВМ реализующая определенный закон управления с целью обеспечения необходимого качества регулирования. Сигналом об ошибке(рассогласование) наз-ся разность м-у заданным и действительным значениями. Системой авт. рег-я наз-ся система служащая для поддержания постоянного значения какой-либо физ. вел. с помощью авт. регуляторов. Такие системы также получили название систем стабилизации. Авт.
управлением наз-ся процесс изменения
по заданному закону какой-либо физ.
вел. с помощью авт. регуляторов, такие
системы получили также название
следящей системы.
Принципы
регулирования. Управление – процесс организации целенаправленного воздействия на объект, в результате которого объект переходит в требуемое состояние. Объект управления подвержен воздействию различных внешних возмущений, вследствие чего управляемая величина отклоняется от заданного значения. Задачей устройства управления является обеспечение соответствия управляемой величины заданному значению путем передачи на ОУ необходимого упр воздействия. Упр по отклонению. Учитывается действительное состояние объекта упр. Явл основным для большинства современных САУ. Недостатки – затруднено упр, возникающее при разработки быстродействующих систем упр. Повышение точности работы у увеличение коэффициента усиления приводит к потере устойчивости.
|
3
О 1. Преобразовывающий элемент – служит для преобразования управляющего воздействия φ(t) в вид энергии для дальнейшего использования. 2 и 5 – элементы сравнения. Эти элементы явл фиктивными, и используются для наглядности структурных схем. В действительности сравнение сигналов происходит на входах усилителей и специальных схем сравнения сигнала. 3. Модем. 4. Последовательное корректирующее устройство, служит для предания системе определенных динамических свойств. 6. Усилитель мощности. 7. Местная отрицательная обратная связь, служит для предания системе определенных динамических свойств. 8. Исполняющее устройство (разл двигатели). 9. Объект регулирования. 10. Главная отрицательная обратная связь. |
|
5. Преобразование Лапласа. Преобразования Лапласа позволяют заменить дифференциальные уравнения алгебраическими. Преобразование определенных уравнений: F(P)=∫f(t)e-ptdt p=b+jw, сокращенный вид: F(p)=L{f(t)} Разработаны правила, доказывающие теорему преобразования Лапласа: 1. Свойство линейности: L{af(t)}=aF(P) L{f1(t)+/-f2(t)}=F1(P)+/-F2(P) 2. Правило интегрирования L{df(f)/dt}=pF(P)-f(0) L{f(t)dt}=F(P)/p Пример: пусть система описывается линейным неоднородным дифуро n-порядка:
В теории управления дифуры записывают так, чтобы в левой части находилась выходная переменная со своими n производными, а в правой входная переменная со своими m производными, такая запись называется стандартной. Найдем изображение по Лапласу (умножим на e-pt и проинтегрируем от 0 до ∞). Обычно САУ рассчитывается при нулевых начальных условиях => все члены, зависящие от начальный условий будут =0.
Данное ур является алгебраическим, из которого можно получить отношение:
отношение выходного сигнала к входному |
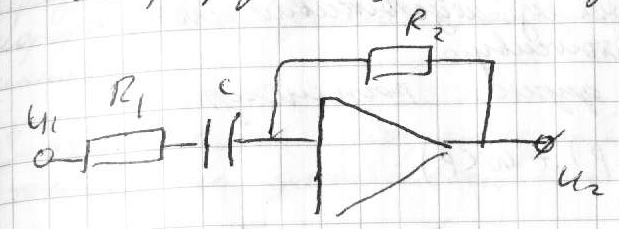
6. Составление уравнения пассивного корректирующего устройства. Н Z1(p) и Z2(p) - комплексные сопротивления. Z(p)=R=LP=1/cp
Корректирующий фильтр: Z(p)=R – резистор Z(p)=LP – индуктивность Z(p)=1/CP - конденсатор
T=RC – постоянная. Зная передаточную функций можно записать дифур элемента: (TP+1)U2=U1
=> TPU2+U2=U1
Решив это уравнение при известном вх сигнале, найдем изменение вых сигнала. |
|
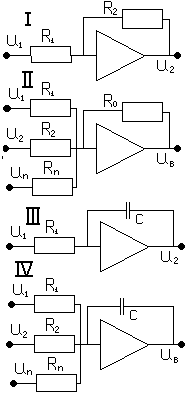
13. Операционные усилители. Операционный усилитель осуществляет математическую операцию умножения на постоянный коэффициент. Т.к. в усилителе выполняются некоторые математические операции, то они получили название операционные усилители. Для наглядности и упрощения схем моделирования, принято на схемах не указывать земляной провод, не показывать источники питания, а коэффициент усиления писать внутри резистора. Виды операционных усилителей: 1. Масштабные.
2. Суммирующие
UВЫХ=-(K1U1+K2U2+…+KnUn) Kn=R0/Ri i=1…n 3. Интегрирующие
4. Интегральный суммирующий
|
9. Составление уравнения активного корректирующего устройства. В общем случае они строятся на базе усилителей постоянного тока. Схема
такого кор устр имеет вид:
Z1(p) - комплексное входное сопротивление, Z(p) – компл сопр цепи обратной связи I1 – входной ток ≈0 ∆U – сигнал ошибки на входе УПТ (УПД будем считать идеальным). УПТ с обратной связью работает как система автоматического управления, по принципу отклонения (сигнал ошибки ∆U≈0). W(p)=-Z2(p)/Z1(p). Активный фильтр: (УПТ имеет два входа)
|
|
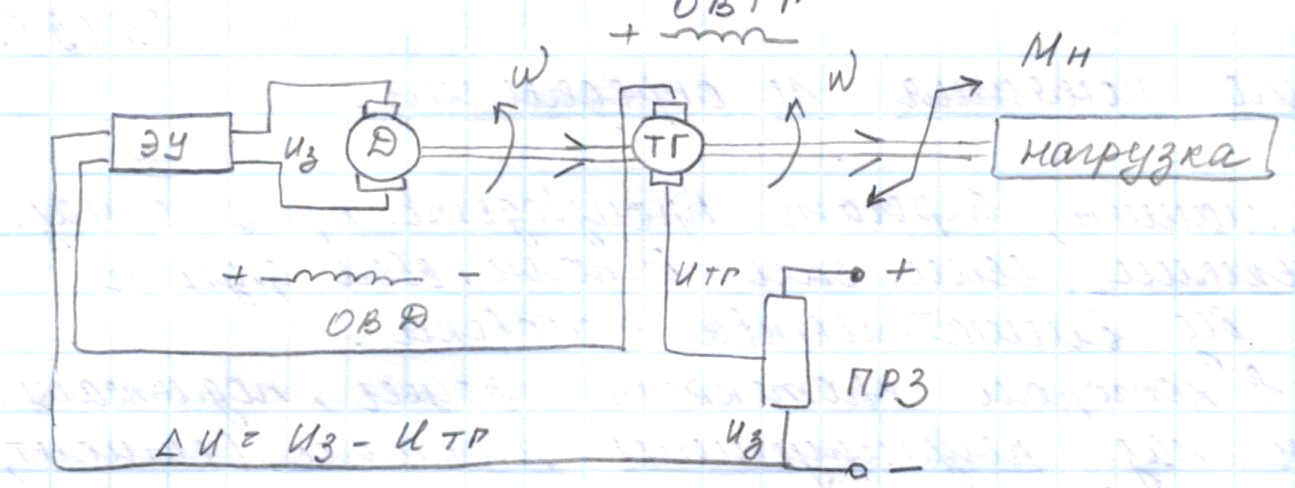
1 переходного режима Следящая система множительно -делительного устройства. ЭУ – электр усилитель. D - двигатель пост тока W - угловая скорость двигателя. Р - понижающий редуктор. α – угол поворота выходного вала редуктора. ПР1 и ПР2 – сдвоенный переменный резистор. UK – напряжение конденсации, т.е. гл отр обратная связь, служащая для формирования сигнала ошибки ∆U. Для облегчения составления уравнения сложной системы ее разделяют на простые элементы и составляют уравнения для каждого из них по отдельности. 1. Уравнение ЭУ Ug=KY∆U=KY(U1-UK) Ky – коэффициент усиления ЭУ. W(p)=Ky 2. Уравнение D: TЭТМР2W+ TЭРW+W=KgUg W(p)=Kg/(TЭТМР2+ TЭР+1) TЭ – электромагнитная постоянная тока (с),ТМ – электромеханическая пост времени (с), Кg – коэффициент передачи двигателя. 3. Уравнение редуктора WP=KPW WP – угловая скорость на выходе редуктора. КР – коэффициент передачи редуктора. WP=dα/dt=Pα Pα =KPW W(p)=KP/P 4. Уравнение ПР1 UK=IRX=U2RX/Rn, т.к. резисторы линейные, то для них сравнивается отношение RX/RM=α/αMAX, где αMAX – макс угол поворота двигателя ПР1 UK=αU2/αMAX=Kn α Kn=U2/αMAX Kn- коэффициент передачи. W(P)=Kn По опр передаточной ф-ции имеем UK=KnKP(U1-UK)/(Р(T2P+1)(T1P+1)), приводим это уравнение к стандартной форме: [Р(T2P+1)(T1P+1)+К]UK=KU1 K=KY Kg Kn KP
|
15. Структурный метод моделирования (СММ). Система уравнений практически любой степени сложности состоит из ограниченного числа типовых элементов САУ. К ним относятся: 1. Усилительное звено W(P)=K 2.
Инерционное звено
Если ξ=0 звено наз-ся консервативным, на выходе возникают незатухающие колебания 4.
Идеальное интегрирующее звено
5. Идеальное дифференцирующее звено W(P)=KP Таких звеньев в природе нет, они входят в другие передаточные функции. 6.Реальное
дифференцирующее звено
7.
Инерционное интегрирующее звено
Для каждого типового звена составлена его электронная модель, и в соответствии со СММ в исходной структурной схеме каждое типовое звено заменяется соответствующей электронной моделью, которая соединяется между собой в соответствии со структурной схемой. |
|
14. Моделирование САУ по дифуру.
Алгоритм составления схемы для решения этого уравнения: 1. Запишем ур-е в операторной форме: T2T1P3+(T1+T2)P2UK+ PUK+KUK=KU1 2. Решим уравнение относительно старшей производной (найдем P3UK):
3. Будем считать, что нам известна правая часть этого ур-я. Т.к. U1 необходимо умножить на К1, то это делают с помощью масштабного опер усилителя –К2Р2UK , который тоже умножается на К2. Просуммировав получившиеся величины с помощью суммирующего опер усил на выходе получим сигнал -P3UK, Совместим операцию суммирования с опер интегрирования и на выходе получим 1/Р, затем интегрируем, пока не получим сигнал UK. |
16. Модель инерционного звена.
Решим уравнение относительно каждой производной
Cчитая известной правую часть составим схему для моделирования:
|
|
17. Модель колебательного звена.
Решим относительно старших производной
Cчитая известной правую часть составим схему для моделирования:
|
18. Модель реального дифференцирующего звена.
Cчитая известной правую часть составим схему для моделирования:
|
|
24. Необходимое и достаточное условие устойчивости. Устойчивость-устанавливает факт восхожд. или затух. колеб. в сист., при этом не известно о времени перех. процесса, числе колеб. за время перех. процесса… Сист. будет устойчива если при t->∞, xперех.(t)->0, т.е. процесс затухает. Следоват-но устойчивость определяется только общим решением ур-ия (a0dnxвых(t))/dtn+…+anxвых(t)= (b0dnxвх(t))/dtn+…+bnxвх(t), т.е его левой части и не зависит от вх. сигнала. Составл. харак. ур-ие вида: а0рn+a1pn-1+…+an=0; В Для сист. высокого порядка находить корни хар-го ур-ия сложно, поэтому разработаны спец. правила.
|
20. Преобразование структурных схем. Используется для упрощения анализа САУ, составления передаточных функций и дифференцианальных уравнений. Последовательное соединение звеньев. При последовательном соединении звеньев передаточная функция системы равна произведению передаточных функций звеньев, входящих в систему. Параллельное включение звеньев. Переходная характеристика системы равна сумме переходных характеристик звеньев. Встречно-параллельное соединение динамических звеньев. К
Контур с положительной обратной связью
|
|
21. Связь между различными передаточными функциями. W(Р) – передаточная функция разомкнутой системы. WP(P) - передаточная функция разомкнутой системы без учета обратной связи. Ф(Р) - передаточная функция замкнутой системы. WF(P) - передаточная функция по возмещению воздействия. WX(P) - передаточная функция ошибки. g(t) – входной сигнал, y(t) – выходной, f(t) –сигнал обратной связи. W(P)=WP(P)W0(P)
Ошибка системы равна: x(t)=g(t)-y(t)
|
22. Частотные характеристики. Частотные характеристики (ЧХ) определяют динамические свойства звена или системы. Если на вход разомкнутой системы подать гармонический сигнал XBX=XBXSIN(ωt). При прохождении гармонического сигнала ч/з лин сис происходят амплитудные и фазовые искажения, которые можно определить при помощи ЧХ. ХВЫХ=XBЫX SIN(ωt+φ). Заменим вх и вых сигналы на их изображение в виде комплексных чисел: XBX=XBXеJ(ωt) ХВЫХ=XBЫX eJ(ωt+φ) W(Jω) – комплексная частотная ф-ця (аналогия передаточной ф-ции), которая получила название амплитудно-фазовой ЧХ (АФК). W(Jω)=A(ω)eJφ(ω) A(ω) – амплитудная ЧХ (АЧХ), φ(ω) – фазовая частотная х-ка (ФЧХ). W(Jω) представляет собой комплексное число, в ней можно выделить вещественную и линейную часть - W(Jω)=U(ω)+JV(ω). U(ω) – вещественная ЧХ (ВЧХ), V(ω) – линейная ЧХ (ЛЧХ). Тогда:
Прологарифмируем W(Jω)=A(ω)eJφ(ω) => lnW(Jω)=lnA(ω)+Jφ(ω) – логарифмическая ЧХ LnA(ω) – логарифм амплитудная х-ка (ЛАХ), φ(ω) – логарифмическая фазовая х-ка. ЧХ позволяют опр источник сигнала, оценивать качество переходного процесса, опр точность САУ, осуществлять синтез корректирующего устройства. |
|
42. Жёсткие обратные связи. Обратная связь – устройство, передающ. возд. от какого-либо последующ. Элемента на вход одного из предыдущ. звеньев и по методу присоединения делятся на положит. и отрицат. Простая жёсткая обр. связь описывается уравн. Yoc=Koc+Xoc WKoc(p)=Koc Пусть имеется усил-ль мощности с коэфф. усил-я 10 (рис1). Усил-ль с таким коэфф. усил-я можно получить, если ввести предварит. Усил-ль и охватить их жёстк. Обр. cв-ю. (рис2) В следствие старения элементов нестабильности источника питания и т.д. коэфф. усил-я мощности изм. В 2 раза и стал равен 5. А в усил-ле, охв. Обр. св., коэфф усил-я будет равн 9,9. За счёт обр. связи можно значит. Снизить влияние нестабильности параметров охватываемого звена. Охватим инерц. Звено простой ЖОС (рис3)
За счёт выбора Кос можно существенно уменьш. Инерц-ть охватываемого звена, что повышает запас устойчивости и быстродействия системы, но во столько же раз уменьшается коэфф. усил-я, что приведёт к понижению точности системы, а это недопустимо, потребуются дополнительные каскады усиления, это приведёт к повышению стоимости, габаритов, к уменьшению надёжности. Можно охватывать ЖОС разные звенья. (примеры приведены в лекции), выполнено аналогично.
|
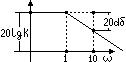
29 . Частотные х-ки идеального интегрирующего звена. 1.
Амплит фазовые х-ки: W(P)=K/P
P=Jω
2.
Амплитудные частотные характеристики: 3.
фазовая частотная характеристики:
4.
Логарифм амплит х-ки:
L(ω)=20lgA(ω)=20lg(K/ω)=20lgK-20lgω L(ω=1)=20lgK. Приращение ординаты при изменении частоты на одну декаду: L(10ω)-L(ω)=20lgK-20lg10-20lgω-20lgK+20lgω=20dδ
|
|
30. Частотные х-ки идеального дифференцирующего звена. 1. Амплит фазовые х-ки: W(P)=KP P=Jω W(Jω)=JKω U(ω)=0 V(ω)=Kω 2.
Амплитудные частотные характеристики: 3.
фазовая частотная характеристики:
4.
Логарифм амплит х-ки:
L(ω)=20lgA(ω)=20lgKω=20lgK+20lgω L(ω=1)=20lgK. Приращение ординаты при изменении частоты на одну декаду: L(10ω)-L(ω)=20lgK+20lg10+20lgω-20lgK-20lgω=20dδ
|
31. Частотные х-ки инерционного звена. 1.
Амплит фазовые х-ки:
2.
Амплитудные частотные хар-ки: 3.
фазовая частотная характеристики:
4.Лог
ампл х-ки:
Приращение
ординаты при изменении
частоты на одну декаду (ω=1/Т):
|
|
32. Построение ЛАХ и ЛФК разомкнутой системы (РС). Наиболее простые системы получаются если передаточную функцию РС можно привести к виду (А - кол-во интегрирующих звеньев W(P)=1/P):
Правило построения ЛАХ РС. На низких частотах пренебрегают всеми постоянными времени и рассматривают передаточную функцию W(P)=K/PA. Для построения ЛАХ этого звена из (.), где ω=1, восстанавливаем перпендикуляр = 20 lgK и ч/з получившуюся (.) проводим прямую с наклоном -20Adδ/дек. Эту асимптоту проводим до первой сопрягающей частоты ωi=1/Тi ωJ=1/ТJ , если эта сопрягающая частота соответствует постоянной времени находящийся в знаменателе (что соответствует интегрирующему звену 1/(ТР+1), наклон ЛАХ которого равен -20 dδ/дек). То ЛАХ опускается вниз и проводится до следующей сопрягающей частоты. Если эта сопрягающая частота соотв постоянной времени находящийся в числителе (что соответствует дифференцирующему звену ТР+1, наклон ЛАХ которого равен +20 dδ/дек). То ЛАХ поднимается вверх до следующей сопрягающей частоты и т.д. ЛФК
строится по перемножению, т.к. при
перемножении комплексных чисел
аргументы складываются:
|
44. Гибкие обратные связи. Гибкие обратные связи – исчезающие, т.к. они действуют только во время переходного процесса. Охватим простое инерционное звено гибкой обратной связью (рис1)
При таком охвате тип звена не изменился, что очень важно, так как сохранился порядок астатизма, а за счёт выбора Кос можно существенно уменьшить инерционность звена, что позволяет повысить запас устойчивости и быстродействие системы, но при этом уменьшается коэффициент усиления системы, что недопустимо, поэтому потребуются дополнительные каскады усиления. Охватим инерционное звено простой гибкой ОС (рис2)
Увеличивается постоянная времени охватываемого звена, уменьшается запас устойчивости и быстродействия, поэтому не всякая ОС может дать положительный эффект.
|
|
25. Критерий устойчивости Гурвица. Критерий разработан в 1895г. Пусть
определено характеристическое
уравнение замкнутой системы:
Составим главный определитель Гурвица по следующему правилу: по главной диагонали записываются коэффициенты уравнения, начиная со второго по последний, столбцы вверх от диагонали заполняются коэффициентами с возрастающими индексами, а столбцы вниз от диагонали - коэффициентами с убывающими индексами. Остальные места заполняются нулями. В случае отсутствия в уравнении какого-либо коэффициента и вместо коэффициентов с индексами меньше 0 и больше n пишут нуль. Системы первого и второго порядка устойчивы, если все коэффициенты характеристического уравнения больше нуля. Система
находится на грани устойчивости, если
Если
Если хотя бы один из коэффициентов или один из определителей отрицательны, то система устойчива. Если один из коэффициентов либо один из определителей равны нулю, то система на грани устойчивости. Критерий Гурвица удобен для исследования устойчивости систем третьего и четвертого порядков, когда известны параметры системы. |
26. Пример критерия Гурвица. Передат. ф-я разомк. сист.равна:W(p)=(kykgkpkn)/((T1p+1) (T2p+1)p)=k/((T1p+1) (T2p+1)p) Передат. ф-я замкн. сист. Ф(р)=W(p)/(W(p)+1)=k/((T1p+1) (T2p+1)p+k) Тогда харак. ур-ие: Т1Т2р3+( Т1 +Т2)р2+р+к=0
|
|
27. Критерий устойчивости Михайлова. Устойчивость
замкнутой САУ определяется
характеристическим полиномом:
Согласно
принципу аргумента для устойчивой
системы
При
изменении
от
Можно
показать, что функция u()
четная, а ()
нечетная. Поэтому
Формулировка
критерия Михайлова.
Система устойчива, если при изменении
от 0 до
|
37.Коэффициенты ошибок. Существует более простой способ определения ошибок в установившихся и вынужденных режимах. Этот путь состоит в определении коэффициентов ошибок C0,С1,… Передаточная функция ошибки Wx(p)=x(t)/g(t)=1/1+w(p). X(t)=1/1+w(p) g(t)=(C0+C1p+(C2/2!)p2+…)g(t) (1) xуст = C0g(t)+C1dg(t)/dt+C2/2! d2 g(t)/dt2 ,т.о зная коэф-ы ошибок и зная измене g(i)можно определить ошибки в установ. и вынужден. Режимах, коэф-ы ошибок легко получить если разделить числитель передаточ. Функ-и ошибки на знаменатель и сравнить полученный ряд с (1) |
|
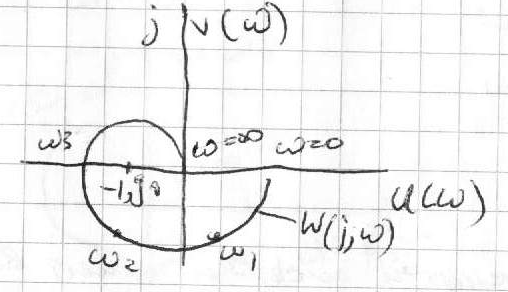
28. Критерий устойчивости Найквиста. Критерий базируется на частотных характеристиках разомкнутой цепи САУ, так как по виду частотных характеристик разомкнутой цепи можно судить об устойчивости замкнутой системы. Система, устойчивая в разомкнутом состоянии. Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи не охватывала точку (-1, j0). С Система с неустойчивой разомкнутой цепью. Для устойчивости замкнутой системы требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи (с дополнением в бесконечности для нейтральных систем) охватывала точку (-1, j0) против часовой стрелки на угол m, где m - число полюсов с положительной вещественной частью в передаточной функции неустойчивой разомкнутой цепи системы.
|
4.Понятие об элементе САУ Реальная
система управ. Состоит из некоторго
кол-ва элементов определенным образом
соедин. Между собой каждый элемент
имеет выход и вход (обозн. стрелками). |
|
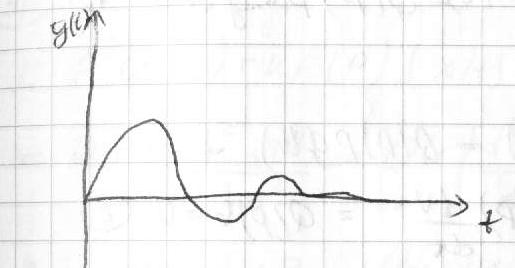
34. Понятие о качестве переходного процесса. Основным показателем, определяющем пригодность системы к эксплуатации является устойчивость. Но устойчивая система может иметь не достаточное быстродействие, большое число колебаний, недостаточную точность. Для каждого случая пригодность системы определяется точностью и характером переходного процесса. Точность САУ хар-ся величинами ошибок, в установившихся и вынужденных режимах, которые имеют место после окончания переходного процесса. Переходный процесс принято рассматривать как реакцию системы на единичный ступенчатый сигнал, характеризующий наиболее тяжелый режим работы системы. О tn - это время, по истечению которого выходная величина становится < заданной величины ∆ (обычно ∆=(5-10)% от входного сигнала). Для определение качественных показателей по кривой переходного процесса требует решения дифуров, а при выборе параметра требует решения нескольких дифуров, поэтому разработаны приближенные оценки кач-ва переходного пр, которые не требуют решения дифуров. |
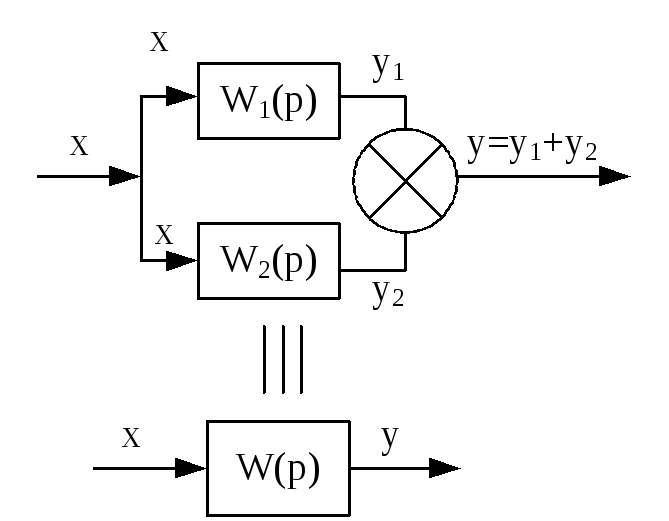
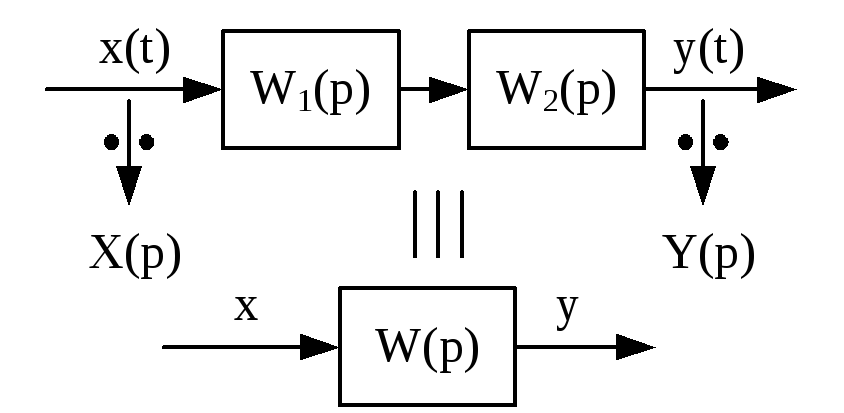
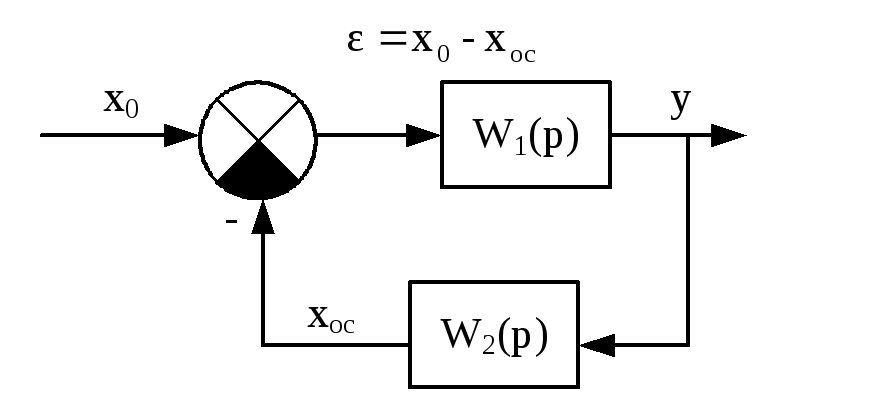
19.Передаточная функция послед,парал,охвач.обрат.связь. Для этого используются следующие правила: 1) последовательное соединение элементов системы, где W(p) = W1(p)·W2(p) – см. рисунок слева. 2) параллельное соединение звеньев, где W(p) = W1(p) + W2(p) – см. рисунок в центре. 3) Антипараллельное соединение с отрицательное обратной связью – см. рисунок справа.
3) Y(p) = W1(p)·ε(p) = W1(p)·[X0(p) – Xос(p)] = W1(p)·[X0(p) – W2(p)·Y(p)], тогда (1 + W1(p)·W2(p))·Y(p) = W1(p)·X0(p); Y(p) = X0(p) · W1 / (1 + W1·W2) => W(p) = W1(p) / (1 + W1(p)·W2(p)) – эквивалентная передаточная функция. Замечание: если обратная связь будет положительной, то знак в знаменателе будет заменен на «–».
|
|
2. . Принципы регулирования. Управление – процесс организации целенаправленного воздействия на объект, в результате которого объект переходит в требуемое состояние. Объект управления подвержен воздействию различных внешних возмущений, вследствие чего управляемая величина отклоняется от заданного значения. Задачей устройства управления является обеспечение соответствия управляемой величины заданному значению путем передачи на ОУ необходимого упр воздействия. Упр по возмущению. Основано на принципе компенсации возмущений. Управляемый параметр не изменяется, а используется информация о внешнем воздействии. Достоинство – имеется возможность полной компенсации возмущения. Недостаток – нет требуемой точности. Комбинированное упр. Более высокое качество упр, т. к. информация о значении возмущающего воздействия позволяет устройству упр работать с предвидением , т.е. начинать компенсацию внешнего возмущения, нарушающего нормальную работу объекта упр, раньше чем возникает достаточно большое отклонение. |
7.Составить уравнения коректируещего фильтра.
|
|
23. Логарифмические частотные характеристики. При проектирование САУ широко распрастранены логарифмические частотные характеристики, а основанием являеться то логарифмические чатотные характеристики строяться практически без вычислений пролагорифмируем выражение: W9jw)=A(w)*e^(jфи(w)); ln(w(jw))=ln(A(w))+jфи(w) ; ln(a(w)) называется логарифйфмичекой амплитудной частотной характеристикой; ln(A(w)) ЛАХ; фи(w) логарифмическая фазовая харктеристика(ЛФХ) на практике для удобства построение ЛАХ использеуться не LN(A(w)), а пропоциональная ей велина 20 lg(A(W)) которая измеряеться дБ и обозначаеться Lдб(W)=20lg(A(w)) 1 бел – соответсвует 10 раз. 2бела – 100 . Тк величина Белл больше то ипользуеться 0,1 для постоения ЛАХ и ЛФК ипользеться стандартная логарифмическая сетка по оси Х которая откладываеться логарифмичекой чатоты lg(w) , а для удобства около меток пишется само знакчение частоты мастаб получеться неравномерный в начале координат пишеиться любое значение частоты отличное от 0 lg=-бесконечности. По
оси Х вводяться единицы октавы и декады
.1 октава соответсвует *2-нию частоты,
1 декада соотеветсвует *10 частоты
относительно декад мастаб получеться
равномерный по Y
откладываеться дБ
|
12. Составление уравгнения двигшателя постянного тока под двигетелем постянного тока записываем дифур. ТэТм=(E^2*W(T)/dt)+(Tэ*W(T))/dt+w(t) =KgUg(t), Тэ,с – электромагнитая постоянная тока , Тм,с – электрлмагнитная потоянная времени, Kg – коэффициент пердачи двигателя. Уравнение: ТэТмP^2W+ ТэPW+W=KgUg. W(p)=Kg/( ТэТмP^2+ ТэP+1) р
|
|
8 Передаточноая функция УПТ охваченного глубокой отрицательной обратной связью С Z1(p) – комплексное входящее сопртивление Z2(p)- комплексное сопротивлении цепи обратной отрицательнйо. i вх – входной ток УПТ т к УПТ в данном случае работает как автомат. система с отрицательной обратной то сигнал ошибки ΔU будет равен 0 а т к R вх стремиться к бесконечности i вх = 0 поътому потенциал (*) а = потенциалу (*) b (1)U2=Z2(p)*i2; i2=i1 по 2-ому закону кирхгова имеем Z1(p)i1+U1=0; i1=i2=-U1/(Z1(p)); U2=-Z2(p)*U1/Z1(p) ; w(p) =U2/U1=-Z2(p)/(Z1(p)); «-« показывает что происходит инверториванние вх сигнала. Включая во входящую цепь и в цепь обратной связи различно Z1(p),Z2(p) можно получить сотни различных типов активных корректирцюющих устройств. Такая схема включения УПТ нашла широкое применение для моделирования САУ на ЭВМ. |
10.Составить уравнения активного корректирующего устройства.
|
|
33. Логарифмические критерии устойчивости Исследование устойчивости по критериям Найквиста можно осуществить по амплитудно-фазово-частотным характеристикам Пусть АФХ разомкнутой системы имеет вид Поэтому такому начертанию АФХ будет соответствовать следующее расположение
Пусть АФХ разомкнутой системы имеет вид 1 (рис)
Согласно критериям Найквиста замкнутая система будет устойчива
Поэтому такому построению АФХ будет соответствовать ЛАХ и ЛФК
Пусть АФХ разомкнутой системы имеет вид
Для
устойчивости линейной системы n-го
порядка необходимо и достаточно, чтобы
для всех частот, при которых ЛАХ>0
ЛФК не пересекали линию
|
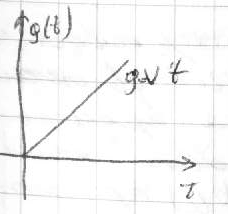
36.Точность САУ в типовых режимах (движение с постоянной …). Этот режим может сущ-ть при изменении управляющего воздействия с пост.скоростью. g(t)=vt, v=const
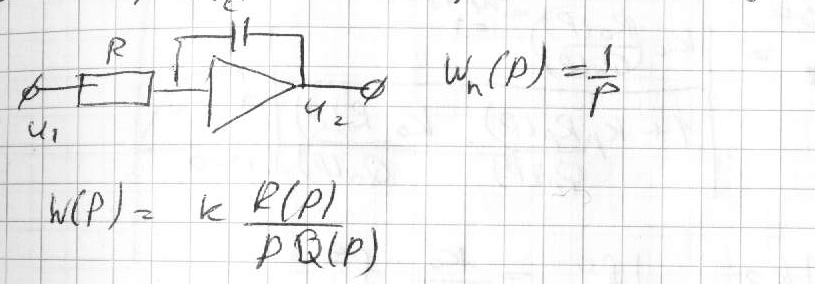
Такой сигнал явл-ся типовым при исслед-нии и проектир-нии следящей с-мы.Ошибка с-мы в этом режиме наз-ся скоростной x(t)=xск. V и xск задаются в ТЗ на проектир-ние,исходя из конкретного технологического процесса. Найдем диф.ур. для ошибки,используя передат.ф-ию ошибки. Wx(p)=x(t)/g(t)=1/(1+W(p)). В общем случае: W(p)=kR(p)/[pQ(p)], где - кол-во интегрир.звеньев или порядок астатизма. x(t)/g(t)=1/(1+kR(p)/[pQ(p)]=Q(P)P/(PQ(P)+k R(P)); (PQ(P)+kR(P))X(t)= Q(P)Pg(t).1 случай: =1; [pQ(p)+kR(p)]x(t)=Q(p)pg(t)=Q(p)dg(t)/dt =Q(p)dvt/dt= Q(p)v=v (1). Пусть x(t)=xск=v/k –подставляя это в (1): kv/k=v, т.е.подобранное знач-е явл-ся частным реш-ем ур-я (1)
2
|
|
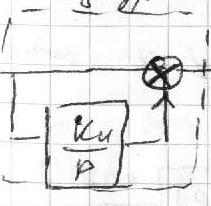
38. Изодромное устройсва. Существует др.путь повышения порядка астатизма без заметного уменьшения запаса устойчивости. Этот путь состоит в применении изодромных устройств. При таком способе дополн.интегр.звено вкл.е последов., в параллельно. Структ.схема САУ в этом сл.будет иметь вид: (рис2)
Wи(p)=1+kи/p=(p+kи)/p=k*(p/kи+1)/p=Tиp+1/Tиp; перед.ф-ия разомкн.с-мы будет равна: W(p)=[kуkиkрkпkд(Tиp+1)]/[(T1p+1)(T2p+1)p2]. Характ.у-е: (T1p+1)(T2p+1)p2+kTиp+k=0. Появился коэф-т при р. Можно обеспечить устойчивость за счет выбора параметров с-мы. Физически это объясняется тем, что изодромное устройство всегда имеет фазовый сдвиг, отличный от -/2 и обратная связь остается отрицательной. из=-/2-arctgTи. порядок астатизма остался=0. Для дальнейшего повышения порядка астатизма можно использовать несколько изодромных устройств.
|
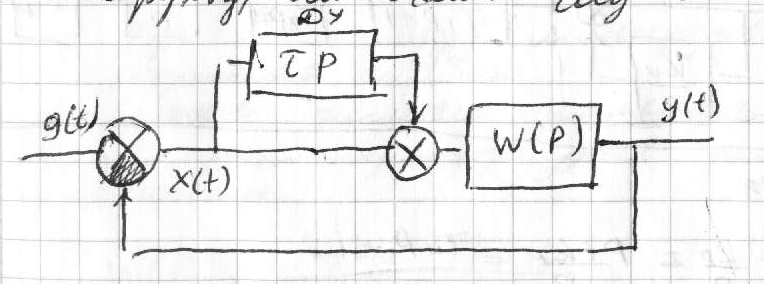
39. Регулирование по производным от ошибок Структурн.схема САУ с введением производной:
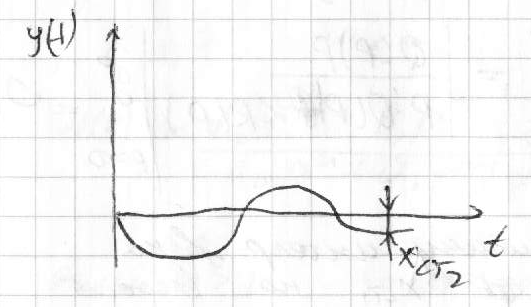
ДУ- диф-ующее устр-во,напр-р диф-щий операц. усилитель W(p)=p/(Tp+1); TС; Пусть перех.процесс для ошибки в с-ме без дифференциатора им.вид(кривая 1): С
|
|
41. Коррекция систем управления Используется не только для обеспечения заданной точности,но и для обеспеч-я желаемого кач-ва переходного проц-са.Различают послед-ные,парал-ные корректир.устр-ва и устр-ва обр.связи. Послед-ные корректирующие устр-ва. Наиболее часто примен-ся,когда в с-ме использ-тся сигнал в виде напряжения пост.тока.Тогда корректир.устр-ва реализ-тся с пом.простых RС-фильтров.Сущ-ют сотни различных типов корректир.устр-в,кот-ые с физ.точки зрения либо усиливают вх.сигнал в определённой полосе частот,либо ослабляют,вносят положит.или отрицат.фазовый сдвиг,что приводит к деформированию АФХ с-мы;и засчёт выбора параметров корректир.устр-в добиваются необходимых запасов устойч-ти по модулю и по фазе.Некот-е виды корректир.устр-в:1.послед-е диф-щее звено;2.послед-е интегродиф.звено. Устр-ва обр.связи - устр-ва,передающие воздействие от какого-л. последующего эл-та на вход одного из предыдущих звеньев,и по методу присоединения дел-ся на положит.и отрицат. Отрицат.обр.связь –такая связь,сигналы кот-ой вводятся в звено со знаком,противоположным знаку поступающего по основной цепи сигнала.Все обр.связи дел-ся на жёсткие и гибкие,кот-ые в свою очередь дел-ся на простые и инерционные.
|
43.Итерационная обратная связь Инерцион.жёстк.обр.связь опис-ся ур-ем: Тос(dYoc/dt)+Yoc=Koc Xoc; Wижос(P)=Koc/(TocP+1). Охватим электронный усилитель ИЖОС.Wохв(P)= K/(1+(KKoc/(TocP+1)))=K(TocP+1)/(TocP+1+KKoc) = K1(TocP+1)/T1P, где K1=K/(1+KKoc),T1=Toc/(1+K Koc).
X2 X1
Cигнал на выходе будет пропорционален входному сигналу и производной от вх.сигнала,т.е. с пом.этой схемы вводятся производные в закон управл-я,что повышает запас устойч-ти и быстродействие с-мы. Т.о.,обр.связи позволяют реализовывать сложные законы управл-я
|
|
40. Комбенирвоаное управление. Под комбенированным управлением понимается такой способ построения автоматических систем, когда, наряду с регулированием по одклонению, используется регулирование по управляющему и возмущающему воздействию. Внешние воздействия длеятся на задающие, сигнал которых система должна воспроизводить, и возмущающие, действия которых система должна скомпенсировать. Структурная схема комбенированной САУ по задающему воздействию изобр на рис. Здесь наряду с сигналом ошибки Х(т), во внутреннюю цепь системы вводится сигнал задающего воздействия г(т) через некоторую передаточную функцию фи(п) При фи(п)=0 передаточная функция замкнутой системы равна Ф(р)=W(p)/1+W(p) При фи не равном 0 Y(t)=W(p)[f(p)g(t)+g(t)-y(t)] Откуда Фэ=[1+f(p)]W(p)/(1+W(p)) Где Фэ(р) эквивалентная передаточная функция замкнутой системы (с учетом разомкнутого контура). Сравнивая уравнения 1 и 2 можно заметить, что они имеют одно и то же характеристическое уравнение замкнутой системы 1+W(p)=0 а следовательно, введение регулирования по задающему воздействию не влияет на устойчивость. Передаточную функцию ошибки можно найти по уравнению Wхэ=1-Фэ(р)= 1-f(p)W(p)/1+W(p) установившаяся ошибка бедет равна нулю при любой форме задающего воздействия в том случае если фи от п рана 1 деленой на даблв от п. Разложив это уравнение в степенной ряд получим Фи(п)=Ф0+т1р+т2квадратт3куб+… где А0 безмерное число Таким образом, при введении регулирования по задающему воздействию (для получения полной инвариантности) необходимо вводить первую и выше производные от задающего воздействия. Практически, точно можно ввести только первую производную а остальные могут быть получены толко приблезительно. Поэтому, может быть получена не полная а часная инвариантность Так, например, введением первой производной можно получить скоросную ошибку, равную 0, то есть повысить порядок астатизма на единицу. Аналагичный результат получится при введении интегрирующих звеньев, но при этом уменьшается запас устойчивости и система может стать неустойчивой. Как показано выше, при комбенированном управлении фи(р) не влияет на устойчивость. Вводя первую и вторую производную, можно повысить порядок астатизма на два и тд Комбенированное управление может быть использовано также для снижения ошибки от возмущающего воздействия (рис) Передаточная функция по возмущению будет иметь вид
Условие полной инвариантности может быть получено, если положить Фф(р)=0 Тогда Как и в случае использования регулирования по задающему воздействию получение полной инвариантности затруднено из за необходимости вводить первую и более высокие производные от возмущения…. |
35 Точность САУ в типовых режимах (неподвижное состояние) Этот режим может сущ-ть при постоянных управляющих и возмещающих воздействиях. g(t)=g0=const; f(t)=f 0=const; При отработке этих сигналов появ-ся ошибка x(t), кот-ая получила название статической,а т.к. все производные от пост.величин=0, то P=d/dt=0; С-мы,кот-ые имеют статич.ошибку,получили название статических с-м.Найдём выражение для ошибки из обобщенной структурн схемы САУ, кот-ая им.вид (рис)
Wр(р) – передат.ф-я регулятора; WO(р)-передат.ф-я обьекта регулир-ния. Ошибка равна: x(t)=g(t)-y(t)=g(t)-W0(p)[f(t)+z(t)]=g(t)-W0(p)f(t)-W0(p)Wр(p)x(t); x(t)=g(t)/(1+W(p))+W0(p)f(t)/(1+W(p)); Тогда статич.ошибка будет: xст=|1/(1+W(p))|g0+|W0 (p)/(1+W(p))|f 0=xст1+xст2. При обработке постоянных управляющих и возмущающих воздействий возникают 2 составляющие статич.ошибки. Рассм. 1-ую составляющую Хст. Передат.ф-я разомкн.с-мы в общем случае: W(p)=(b0pm+b1pm-1+…+bm-1p+bm)/(a0pn+a1pn-1+…+an-1p+an); Если m>n,это говорит о физической нереализуемости с-мы,т.к в этом случае должны присутствовать идеальные конденсаторы с W(p)= ĩ p, кот-х в природе нет. W(p)=KR(p)/Q(p). W(0)=K,поэтому xст1=(1/(1+W(0))g0 =g0/(1+K); Для уменьш-я статич.ошибки необх-мо увелич-ть коэф.усиления разомкн.с-мы.Но при этом мы приближаемся к Ккритич и с-ма может стать неустойчивой. Введём преднамеренно в с-му интегрир.звено
Тогда Хст1=0,но интегрир. звено вносит доп.фазовый сдвиг -π/2, что приводит к уменьшению запаса устойч-ти и с-ма может стать неустойчивой.С-мы,кот-ые не имеют статич ошибки наз-ся астатические.При наличии в с-ме n-интегрир.звеньев,с-ма наз-ся астатической n-ого порядка. Рассм.2-ю составл статич ошибки, при этом возможны случаи: объект и регулятор - статические. Wp(p)=Kp*Rp(p)/Qp(p); W0(p)=K0*R0(p)/Q0(p); Тогда xст2=(K0/(1+KpR0))*f0 = K0 f 0/(1+K);
Введём преднамеренно в регулятор интегрир.звено, тогда: Wp(p)=K*Rp(p)/pQp(p); xст2=0; В этом случае имеем:
|

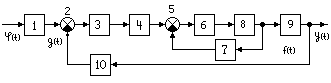 .
Типовая функциональная схема САУ.
.
Типовая функциональная схема САУ.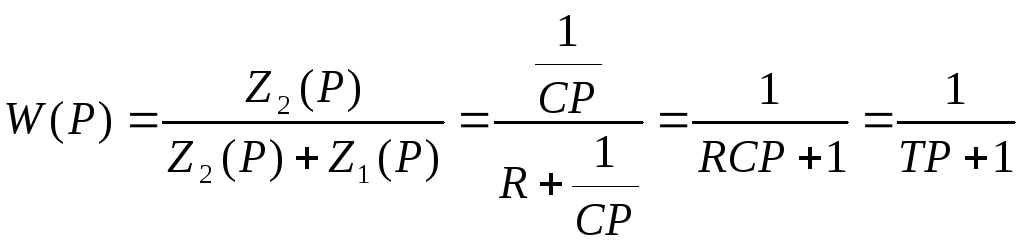
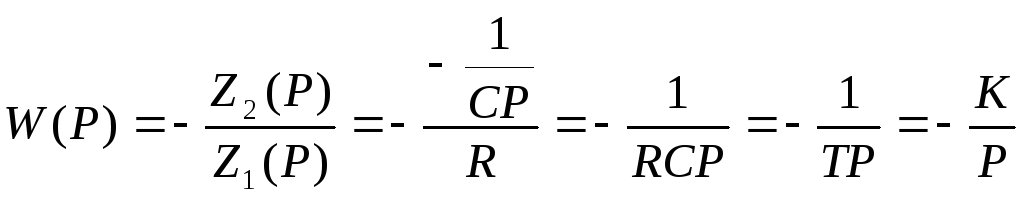 U2=-U1/TP
K=1/T
U2=-U1/TP
K=1/T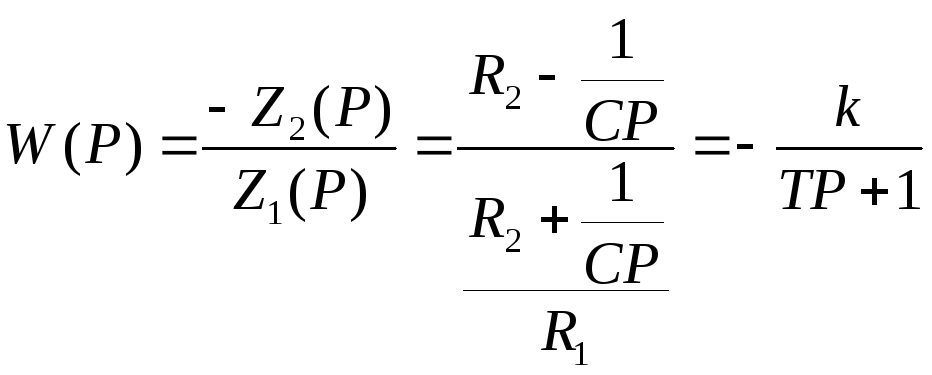 k=R2/R1
T=R2C
k=R2/R1
T=R2C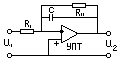 знак (-)
показывает, что происходит инвентирование
знак (-)
показывает, что происходит инвентирование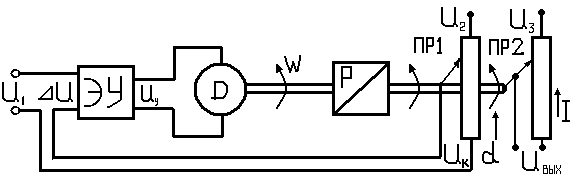 1.
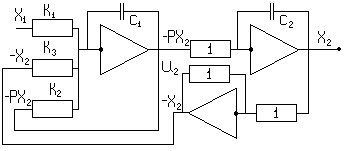
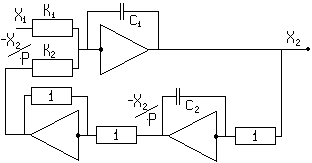
Пример составления уравнений для
1.
Пример составления уравнений для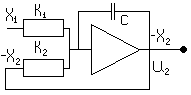
 се
корни харак. ур-ия должны нах-ся в левой
чпсти комплексной полуплоскости Р,
при изменении параметров сист.
изменяются значения корней и корни
мигрируют на комплексную плоскость.
В рез-те чего один или неск-ко корней
могут перейти в правую полупоскость
и сист. будет неустойчивой
се
корни харак. ур-ия должны нах-ся в левой
чпсти комплексной полуплоскости Р,
при изменении параметров сист.
изменяются значения корней и корни
мигрируют на комплексную плоскость.
В рез-те чего один или неск-ко корней
могут перейти в правую полупоскость
и сист. будет неустойчивой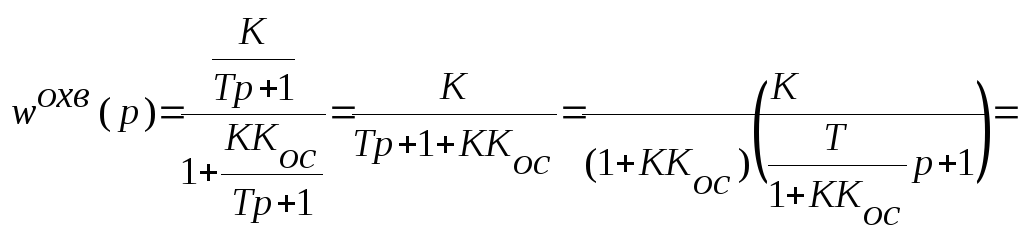
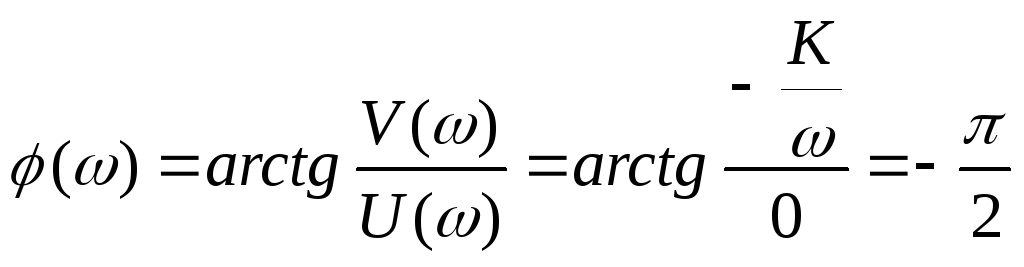
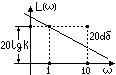 20dδ/дек
20dδ/дек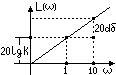
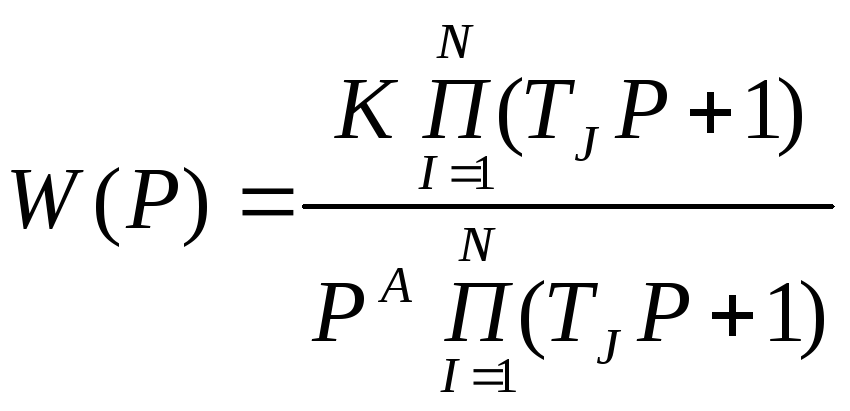 P=Jω
P=Jω
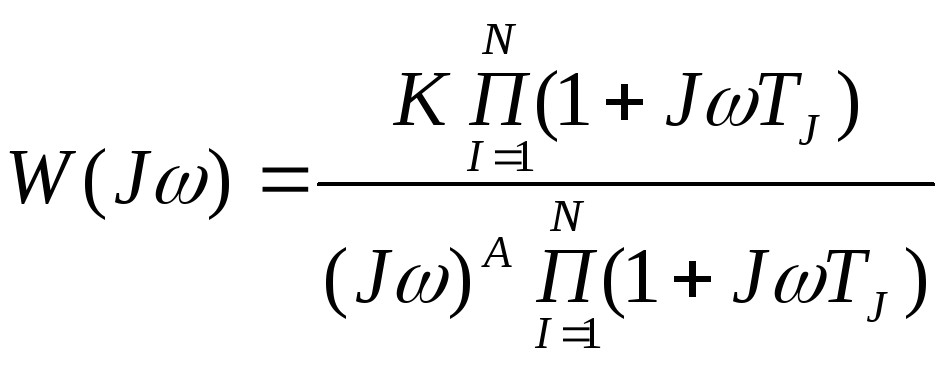 L(ω)=20lg|W(Jω)|
L(ω)=20lg|W(Jω)|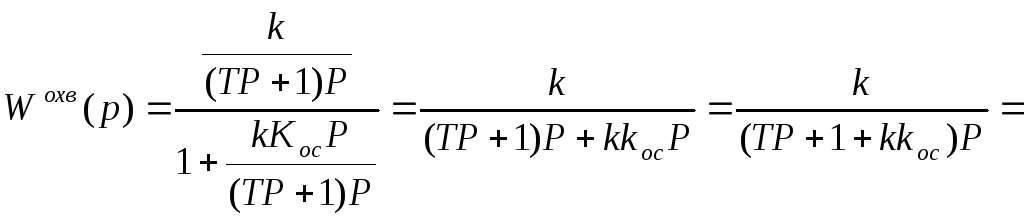
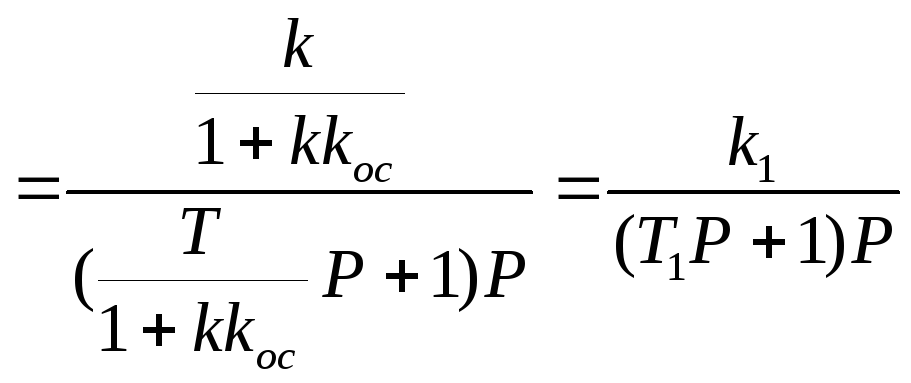
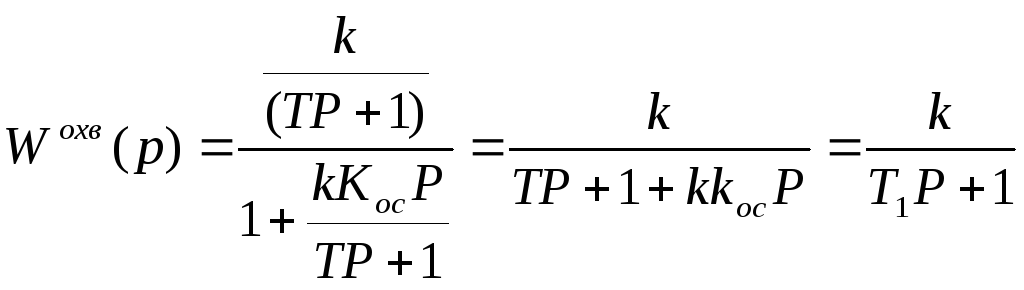
 огда
огда
 истема,
имеющая полюсы на мнимой оси в
разомкнутом состоянии. Если
разомкнутая цепь системы имеет нулевые
и чисто мнимые полюсы, то для устойчивости
замкнутой системы необходимо и
достаточно, чтобы амплитудно-фазовая
частотная характеристика разомкнутой
системы с ее дополнением в бесконечности
не охватывала точку (-1, j0).
истема,
имеющая полюсы на мнимой оси в
разомкнутом состоянии. Если
разомкнутая цепь системы имеет нулевые
и чисто мнимые полюсы, то для устойчивости
замкнутой системы необходимо и
достаточно, чтобы амплитудно-фазовая
частотная характеристика разомкнутой
системы с ее дополнением в бесконечности
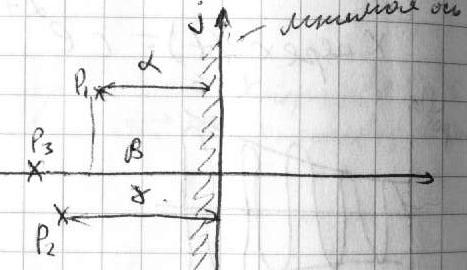
не охватывала точку (-1, j0).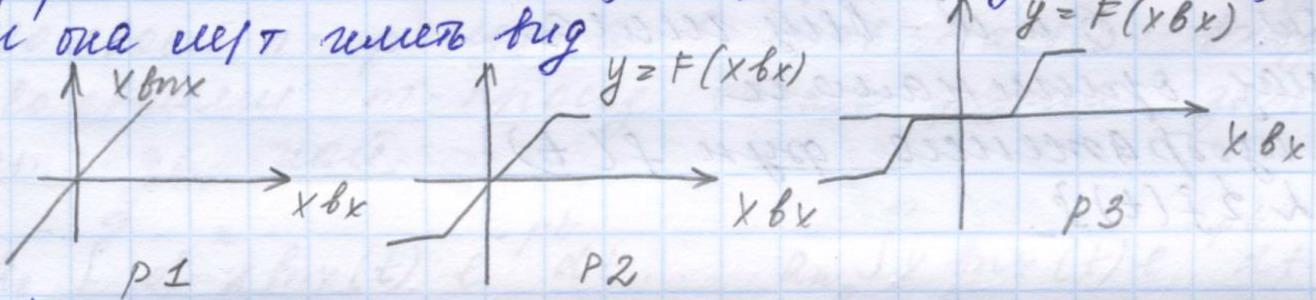 F-нелинейн.статич.
характер.Т.е статич характер. м\б как
линейные Р1 так и нелинейные(вхи вых
имеют одинаковую физ. природу),и
различные(вхи вых не имеют одинаковую
физ. природу). Отношения вых к вх если
их физ прирола одинакова назыв.
Коэф.усиления звена К=Хвых/Хвх, а если
их физич. Природа различна то К назыв.
Коэф. Передачи звена.В общем случае
элемент может иметь несколько вых и
вх в этом случае он назыв. Многосвязаным.Если
вых и вх сигнал элемента изменяет. Во
времени то процесс преобразов.вх
сигнала оописываеться линейным или
нелинейным дифуром.Для
исследован.динамического процесса
САУ необходимо по правилам соответств.
Науки для каждого элемента САУ составить
алгебраические линейн. Или нелиней.
Дифуры полученную систему ура-й
приводят к одному ура-ю связывающ.интересующ.
нас элемент , обычно о вых и вх системы
по получен. Дифур. м\о будет судить о
качестве функций системы.
F-нелинейн.статич.
характер.Т.е статич характер. м\б как
линейные Р1 так и нелинейные(вхи вых
имеют одинаковую физ. природу),и
различные(вхи вых не имеют одинаковую
физ. природу). Отношения вых к вх если
их физ прирола одинакова назыв.
Коэф.усиления звена К=Хвых/Хвх, а если
их физич. Природа различна то К назыв.
Коэф. Передачи звена.В общем случае
элемент может иметь несколько вых и
вх в этом случае он назыв. Многосвязаным.Если
вых и вх сигнал элемента изменяет. Во
времени то процесс преобразов.вх
сигнала оописываеться линейным или
нелинейным дифуром.Для
исследован.динамического процесса
САУ необходимо по правилам соответств.
Науки для каждого элемента САУ составить
алгебраические линейн. Или нелиней.
Дифуры полученную систему ура-й
приводят к одному ура-ю связывающ.интересующ.
нас элемент , обычно о вых и вх системы
по получен. Дифур. м\о будет судить о
качестве функций системы.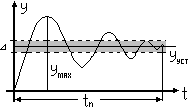 сновными
качественными показателями переходного
процесса явл время переходного процесса
tn
,
перерегулирование δ(%), число колебаний
за время переходного процесса m.
Эти показатель легко определить по
кривой переходного процесса.
сновными
качественными показателями переходного
процесса явл время переходного процесса
tn
,
перерегулирование δ(%), число колебаний
за время переходного процесса m.
Эти показатель легко определить по
кривой переходного процесса.
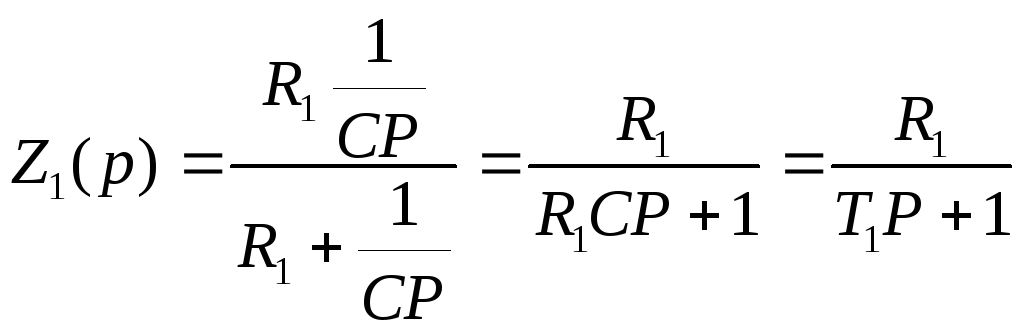
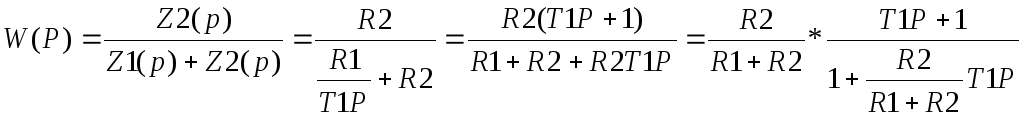
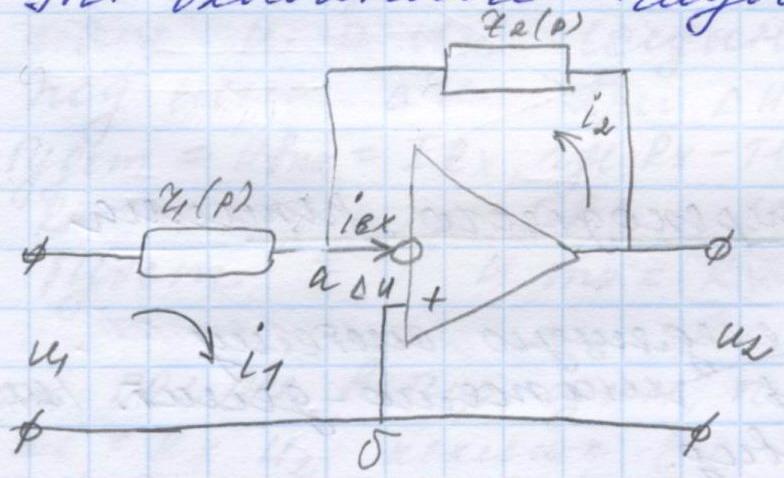 помощь. УПТ… строиться активное
корректирцющее устройство
помощь. УПТ… строиться активное
корректирцющее устройство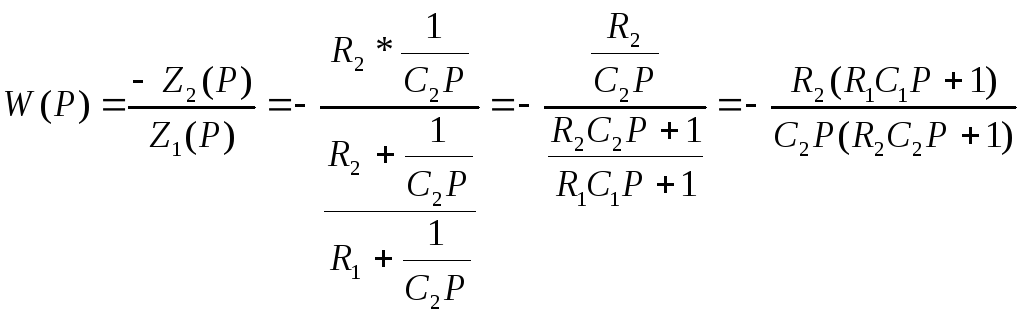
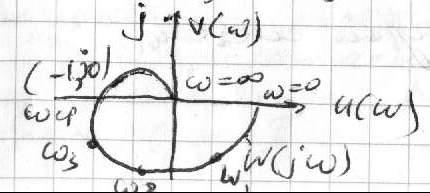 wcp-
частота среза. Это частота, при которой
модуль АФК равен 1 . Согласно критерию
Найквиста замкнутая система будет
находится на границе устойчивости
wcp-
частота среза. Это частота, при которой
модуль АФК равен 1 . Согласно критерию
Найквиста замкнутая система будет
находится на границе устойчивости
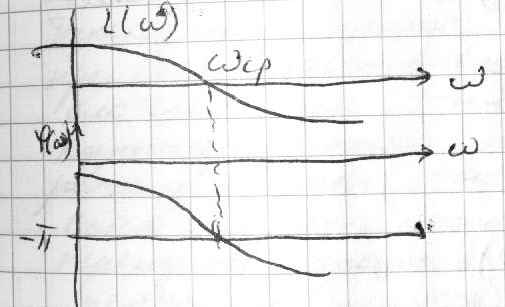
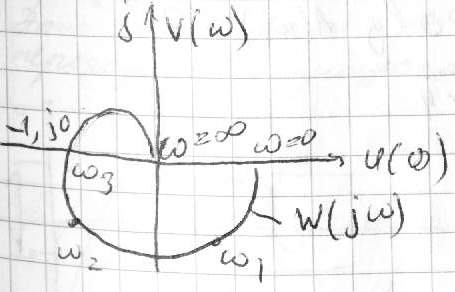


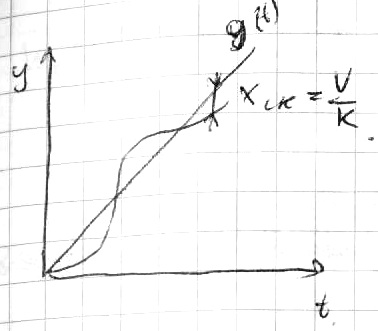
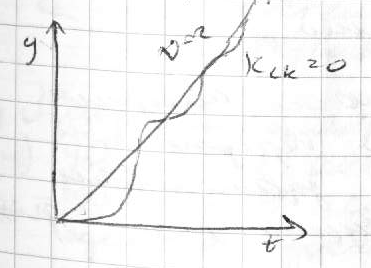 случай:
=2;
[p2Q(p)+
kR(p)]x(t)=Q(p)p2g(t)=Q(p)d2g(t)/dt=
Q(p)d2vt/dt2=0
(2).
Т.к. ур-е (2)
явл-ся однородным, то нет частного
реш-я,=> будет=0 скоростная ошибка,но
2-ое интегрир.звено вносит доп.фазовый
сдвиг -/2,
что приводит к уменьшению запаса
устойч-ти и с-ма может стать
неустойчивой,т.е.сущ-ет противоречие
между устойч-тью и точностью.Перех.процесс
будет им.вид:
случай:
=2;
[p2Q(p)+
kR(p)]x(t)=Q(p)p2g(t)=Q(p)d2g(t)/dt=
Q(p)d2vt/dt2=0
(2).
Т.к. ур-е (2)
явл-ся однородным, то нет частного
реш-я,=> будет=0 скоростная ошибка,но
2-ое интегрир.звено вносит доп.фазовый
сдвиг -/2,
что приводит к уменьшению запаса
устойч-ти и с-ма может стать
неустойчивой,т.е.сущ-ет противоречие
между устойч-тью и точностью.Перех.процесс
будет им.вид:
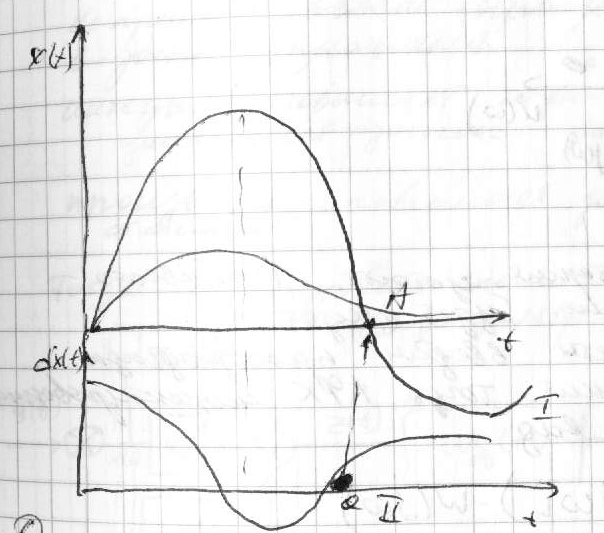 игнал
ошибки=0 в точке А, но вследствие
инерционности эл-тов САУ продолжается
двж в прямом направл-ии.Возникает
ошибка др.знака и возн.колебания.Для
сглаживания колебаний и повышения
быстродействия САУ введем в с-му диф-ее
звено, сигнал к-рого будет изменяться
по закону (кр.2): на участке возрастания
ошибки x(t)
сигналы x(t)
и dx(t)/dt
складываются, что увеличивает порцию
сигнала от регулятора и с-ма начинает
эффективнее обрабатывать ошибку. На
участке уменьшения x(t)
производная меняет знак и вычитается
из сигнала ошибки.В опред.момент
x(t)=dx(t)/dt,а
дальше двж идет по инерции (кривая
3,условно).Т.к.производная повышает
запас устойч-ти,то это позволяет
увеличить коэф-т усил-я с-мы и тем самым
повысить точность.Введение производных
в закон упр-я также позволяет из
неустойчивой с-мы получить устойчивую
игнал
ошибки=0 в точке А, но вследствие
инерционности эл-тов САУ продолжается
двж в прямом направл-ии.Возникает
ошибка др.знака и возн.колебания.Для
сглаживания колебаний и повышения
быстродействия САУ введем в с-му диф-ее
звено, сигнал к-рого будет изменяться
по закону (кр.2): на участке возрастания
ошибки x(t)
сигналы x(t)
и dx(t)/dt
складываются, что увеличивает порцию
сигнала от регулятора и с-ма начинает
эффективнее обрабатывать ошибку. На
участке уменьшения x(t)
производная меняет знак и вычитается
из сигнала ошибки.В опред.момент
x(t)=dx(t)/dt,а
дальше двж идет по инерции (кривая
3,условно).Т.к.производная повышает
запас устойч-ти,то это позволяет
увеличить коэф-т усил-я с-мы и тем самым
повысить точность.Введение производных
в закон упр-я также позволяет из
неустойчивой с-мы получить устойчивую