Лабораторная работа № 4.27

Исследование процессов заряда и разряда конденсатора и определение емкости конденсатора

Цель работы: изучение временной зависимости напряжения на конденсаторе при подключении или отключении источника постоянной ЭДС и определение емкости конденсатора.

Приборы и принадлежности: генератор прямоугольных импульсов, электронный осциллограф, лабораторный стенд с набором конденсаторов и сопротивлений.

Краткие теоретические сведения

Рассмотрим процессы заряда и разряда конденсатора при подключении или отключении источника постоянной ЭДС _о в схеме, представленной на рис.1. Включение и отключение ЭДС имитирует генератор прямоугольных импульсов напряжения. При включении ЭДС (появлении импульса) ток заряда конденсатора протекает по внутреннему сопротивлению источника и по сопротивлению R. Электрические заряды на обкладках конденсатора препятствуют прохождению электрического тока и уменьшают его. Пусть I, Q, U- мгновенные значения силы тока, заряда и напряжения на обкладках конденсатора. Уравнения, связывающие эти величины, имеют вид:

I =, (R+r)I = _o-U, Q = CU. (1)

Исключая в (1) I и U придем к уравнению

. (2)

При решении уравнения учтем начальное условие: Q(0)=0. Это дает решение

, (3)

где  = (R+r)C - постоянная времени цепи заряда конденсатора. Выражение для U получим из связи между зарядом конденсатора и напряжением на его обкладках (рис.2)

. (4)

Прологарифмируем (4)

. (5)

Из (5) следует, что ln(_o/(_o-U)) является линейной функцией времени и по наклону прямой можно определить постоянную времени цепи заряда конденсатора . Зависимость  от сопротивления R также линейная  = (R+r)C и позволяет определить величину емкости конденсатора С и внутреннего сопротивления источника ЭДС - r. Величину  можно определить из (5) как промежуток времени по истечении которого напряжение на конденсаторе достигает величины 0.63_о.

При отключении ЭДС (окончании прямоугольного импульса) ток разряда конденсатора также протекает по сопротивлениям r и R. Для получения закона изменения напряжения на конденсаторе при его разряде достаточно в уравнении (2) положить ₀ = 0 и принять начальное условие Q(0) = ₀C. В результате получим

. (6)

Тогда

(7)

Из (7) следует, что зависимость ln(U_c/₀) от времени, как и в (5), линейная и может быть использована для определения емкости конденсатора.

Описание лабораторной установки.

Генератором прямоугольных импульсов является генератор напряжений ГН1 (выход «меандра»). На лабораторном стенде используются: переменный резистор R, постоянный резистор R₄ и конденсаторы С₁, С₂ и С₃. При использовании цифрового осциллографа ОЦЛ используется канал I.

Порядок выполнения работы.

Часть 1. Проверка закона заряда или разряда конденсатора

1. Собрать схему по рис. 3. Установить значение сопротивления R (по заданию преподавателя) в пределах 500-1500 Ом.

2. Подключить по указанию преподавателя один из конденсаторов С₁, С₂ или С₃.

3. Установить частоту генератора 2500 Гц с помощью кнопки «F» на ГН.

4. Изменяя коэффициент усиления (кнопки «К_ус» и «+» или «-») на осциллографе установить размер изображения по вертикали в пределах 4-7 делений шкалы согласно примеру изображенному на рис.4.

5. Изменяя длительность развертки (кнопки «длит.» и «+» или «-») установить размер изображения заряда или разряда конденсатора по горизонтали в пределах 6-8 делений шкалы.

6. Если изображение не останавливается, можно воспользоваться кнопкой «стоп» и перемещать изображение с помощью кнопок «» и «,».

7. По экрану осциллографа измерить 6-8 пар значений (U_ci - t_i) (см. рис.4,5). Полученные результаты занести в таблицу 1.

8. Для заряда конденсатора построить график зависимости от времени t, для разряда конденсатора график зависимости от времени t. Убедиться, что зависимость носит линейный характер.

9. По наклону прямой определить постоянную времени  которая равняется тангенсу наклона прямой и величину емкости С=/(R₄ + R). Результаты занести в табл.1.

Часть 2. Определение емкости конденсатора по измерению постоянной времени заряда или разряда и определение емкости системы конденсаторов.

1. Определить по экрану осциллографа постоянную времени  которая равняется времени, за которое интенсивность уменьшается в e раз, т.е. U=0.37 U_max , а при зарядке конденсатора 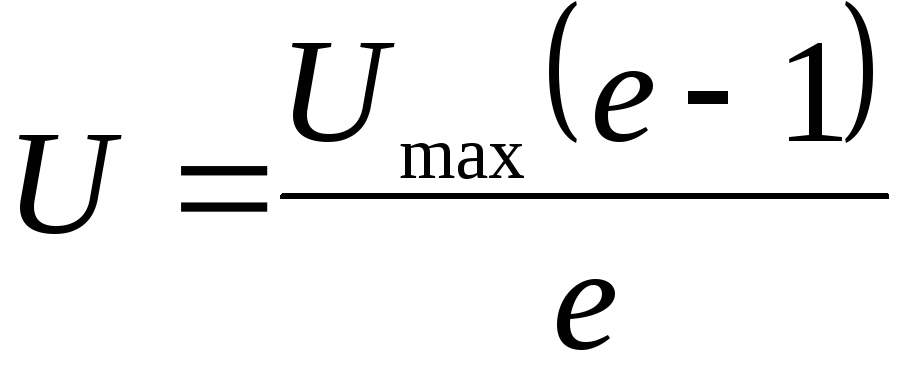=0,63U_max. Этот промежуток времени определяется от начала заряда (разряда) конденсатора до момента, когда напряжение на конденсаторе достигнет величины U_с =0,63 U_max(при заряде) или U_с =0,37 U_max(при разряде) (см. рис. 6). Вычислить емкость С=/(R₄+R), пренебрегая внутренним сопротивлением генератора. Вычислить погрешность С как погрешность при косвенных измерениях, принимая погрешность =0,1дел.длительность развертки. Результаты занести в таблицу 2.

Таблица 1.

Umax=0, дел.	R4, Ом	R, Ом	Номер емкости	Uci, дел.	ti, мкс.			, мкс.	С, мкФ

Заменить измеренную емкость одной из оставшихся (по указанию преподавателя) и повторить измерения по п.1.

2. Провести измерения емкости последовательного и параллельного соединений измеренных конденсаторов по п.1. Сравнить полученные значения с теоретическими значениями при последовательном и параллельном соединении конденсаторов.

Таблица 2.

Номер емкости	(R + R4), Ом	, мкс	С, мкФ	С, мкФ	с, %
Последовательное соединение
Параллельное соединение

Контрольные вопросы

1. Дать определение емкости уединенного проводника и конденсатора.

2. Формула емкости конденсатора: плоского, сферического и цилиндрического.

3. Емкость при последовательном и параллельном соединении конденсаторов.

4. Закон изменения напряжения на конденсаторе при его заряде или разряде.

5. Постоянная времени RC – цепи и метод определения ее в данной работе.