Пример работы программы
Входные данные
Первое множество:
Первая точка (1;1);
Вторая точка (2;3);
Третья точка (3;1);
k=3;
Второе множество:
Первая точка (2;2);
m=1;
Красные точки – первое множество.
Зеленые точки – второе множество.
Графическая иллюстрация
Результат
Центр окружности (2;1.75);
Радиус окружности = 1.25
Синяя точка – центр окружности
Графическая иллюстрация
Анализ правильности решения
Теперь почему решение правильное. В первом примере, при таких точках, радиус окружности должен быть равен 1.25. Давайте проверим.
R
(радиус описанной окружности) =
.
(где S-площадь,
а (a,b,c)-стороны
треугольника).
] а – это сторона между точками (1,1) и (2,3);
b - это сторона между точками (3,1) и (2,3);
c - это сторона между точками (1,1) и (3,1);
Тогда
a
=
=
= b;
c = = 2;
p
(полупериметр) =
=
S=
R=
.
Ответ получен верный.
Рассмотрим второе решение.
Мы ввели в первое множество такие точки (2,2), (4,4), (7,1), (5,-1)
По построению это прямоугольник.
Радиус его описанной окружности должен получиться примерно 2.55.
Чтобы рассчитать его радиус, нам потребуется всего лишь один прямоугольный треугольник, возьмем треугольник с точками (2,2), (4,4), (7,1)
а – это сторона между точками (2,2) и (4,4);
b – это сторона между точками (4,4) и (7,1);
c – это сторона между точками (7,1) и (2,2);
R (радиус описанной окружности) = . (где S-площадь, а (a,b,c)-стороны треугольника).
По следствию теоремы о единственности описанной окружности в треугольнике, мы знаем, что в прямоугольном треугольнике центр описанной окружности находится в середине гипотенузы.
с – гипотенуза.
Центр
окружности
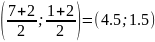
a
b
c
=
6 , т.к. площадь прямоугольного треугольника
= половине произведения длин его катетов.
R
Опять же задача показывает верный результат.