Гбоу "Президентский фмл № 239"

Даны два множества точек на плоскости. Найти центр и радиус окружности, проходящей через k (k>=3) точек первого множества и содержащей строго внутри себя m точек второго множества.

Годовой проект по информатике.

Работу выполнил ученик 10-2 класса

Томчин Анатолий

Учитель информатики:

Батракова Людмила Васильевна.

Учитель геометрии:

Черняев Игорь Владимирович.

Санкт-Петербург

2014

Постановка задачи

По заданным на плоскости координатам вершин n-угольника построить окружность, проходящую через k (k >= 3) точек первого множества и в которой содержатся (не на которой) m точек второго множества.

Информация об исходных и выходных данных

Исходные данные

При вводе сначала задается количество вершин (их должно быть больше или равно трем) n-угольника, а затем координаты по порядку их следования, причем сначала задается абсцисса вершины, а после ордината. Также мы должны ввести числа k (которое меньше или равно количеству точек первого множества) и m (которое меньше или равно количеству точек второго множества).

Выходные данные

На экран должна быть выведена окружность, проходящая через k точек первого множества. Также выведены должны быть координаты центра этой окружности, радиус окружности и какие точки второго множества лежат или не лежат в этой окружности и совпадает ли количество лежащих точек с числом m.

Используемые формулы

Пусть x1, x2, x3, y1, y2, y3: координаты точек соответственно (1-ая точка, 2-ая точка, 3-ая точка);

Пусть x,y: координаты центра окружности.

Уравнений линейной функции

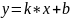
Расчет коэффициентов наклона линии, проходящих через точки

Расчет центра окружности

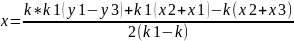
Алгоритм действий

Мы вводим сначала координаты первого множества (больше или равное точкам и до 100 точек). Затем вводим число k, которое обозначает через сколько точек первого множества должна пройти окружность, затем вводим координаты второго множества и число m, которое обозначает, сколько точек второго множества будет лежать в окружности.

Надо выяснить можно ли построить вокруг k точек окружность (например, вокруг k = 3 можно всегда построить окружность), если можно, то высчитываем координаты центра окружности и радиуса окружности. Затем проверяем, действительно ли m точек второго множества лежат в окружности, если да, то пишем, что задача решена, если нет, то редактируем либо точки или их количество, либо m, либо k.