8.Проверка на гладкость.
Кривая,
заданная векторной функцией 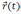 ,
определенной на числовом промежутке
I,
называется гладкой класса
,
определенной на числовом промежутке
I,
называется гладкой класса 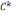 ,
если векторная функция
,
если векторная функция 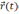 имеет непрерывные производные до порядка
k
включительно и
имеет непрерывные производные до порядка
k
включительно и  .
(В.П.Толстопятов Линии и поверхности в
евклидовом пространстве)
.
(В.П.Толстопятов Линии и поверхности в
евклидовом пространстве)
Следовательно, для того, чтобы показать, является ли параметризация нашей кривой гладкой, нужно решить систему:

Если эта система решений не имеет, то данная параметризация кривой является гладкой.


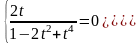
При t=0 система имеет решение. Таким образом, гладкость нарушена в точке O (0;0).Точка возврата I рода.
9.Касательные, параллельные осям координат.
Пусть
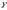 - гладкая кривая, заданная уравнением
- гладкая кривая, заданная уравнением
 .
.
Зафиксируем
точку
 и рассмотрим произвольную прямую
и рассмотрим произвольную прямую
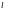 ,
проходящую через эту точку. Пусть
,
проходящую через эту точку. Пусть
 произвольная точка линии
,
произвольная точка линии
,
 – её расстояние до прямой
.
– её расстояние до прямой
.
Прямая
называется касательной
к линии
в точке
 ,
если при стремлении
к
по линии
отношение
,
если при стремлении
к
по линии
отношение
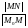 стремится нулю.
стремится нулю.
Имеет место
Т е о р е м а. Гладкая кривая имеет в каждой своей точке касательную, причем единственную.
При
доказательстве этой теоремы расстояние
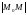 можно найти как длину вектора
можно найти как длину вектора
 и использовать при этом формулу Тэйлора.
и использовать при этом формулу Тэйлора.
Расстояние
можно найти как высоту параллелограмма,
построенного на векторе
и направляющем орте
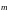 прямой
.
Тоесть
прямой
.
Тоесть
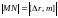 .
.
Тогда
получим, что
 тогда и только тогда, когда
тогда и только тогда, когда
 ,
то есть направляющий орт касательной
коллинеарен вектору
,
то есть направляющий орт касательной
коллинеарен вектору
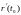 .
Таким образом, направляющим вектором
касательной к гладкой кривой в точке
.
Таким образом, направляющим вектором
касательной к гладкой кривой в точке
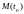 является вектор
.
является вектор
.
а) горизонтальные:


 (0)=(0;
0)
(0)=(0;
0)
(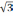 )
=(
)
=( ;
;
 )
)
( )=(
;
)=(
;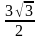 )
)
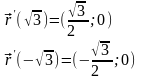
В этих точках горизонтальные касательные касаются графика функции (t).
б) вертикальные

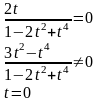
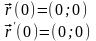
В этих точках вертикальные касательные касаются графика функции (t).
10.Обыкновенные точки, подозреваемые на перегиб.

 считается
непрерывно дифференцируемой в
считается
непрерывно дифференцируемой в 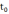 .
.
называется обыкновенной, если  ,
в противном случае точка
-
особая.
,
в противном случае точка
-
особая.
Теорема.
Если
- обыкновенная точка по линии 𝜸,
то прямая l,
проходящая
через 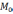 с направляющим вектором определена
однозначно.
с направляющим вектором определена
однозначно.
Пусть
 -
первая, отличная от нуля производная в
точке M
и
-
первая, отличная от нуля производная в
точке M
и  -
первая из производных, неколлинеарных
вектору
-
первая из производных, неколлинеарных
вектору 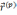 .
Тогда возможны следующие случаи:
.
Тогда возможны следующие случаи:
1) p – нечетное, q – нечетное. Следовательно, M – точка перегиба
2) p – нечетное, , q – четное. Следовательно, образ кривой имеет такой же вид, как окрестность обыкновенной точки.
3) p – четное, q – нечетное. Следовательно, точка M – точка возврата 1 рода.
4) p – четное, q – четное. Следовательно, точка M – точка возврата 2 рода.
Найдем вторую производную:
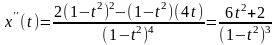

Достаточное условие перегиба:
Первая и вторая производные коллинеарны тогда и только тогда, когда их определитель равен нулю:
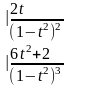
 =0
=0
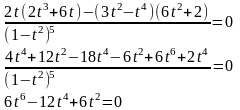
t=0
t=1-эта точка не входит в область определения.
 (0)=(0;0)
(0)=(0;0)
 p=2
p=2
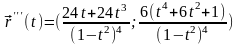
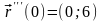
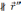 (0)
(0)
 q=3.
q=3.
Получили, что (0)=(0;0) является точкой возврата I рода.
11.Таблица поведения кривой.
-
t
X(t)
Y(t)
k
симметрия кривой относительно оси Ох установлена
0
0
0
точка пересечения с осями
Ох и Оу
+
-1
+
Вертикальная асимптота
-
-1
-
Вертикальная асимптота
y=x-
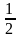 при
при
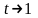
y=-x+ при

Наклонные асимптоты

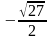
Касательная параллельная Ох
-

Касательная параллельная Ох
0
0
0
Точка возврата I рода
-0,5
0,33
-0,17
Точка пересечения кривой с асимптотой
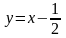
0,5
0,33
0,17
Точка пересечения кривой с асимптотой