2. Статистики сравнения точечных оценок неизвестных генеральных
1) Проверка гипотез для одной выборки
Сравнение |
|
Статистика критерия |
|
Область принятия
|
генеральной средней с утверждением |
известно |
|
|
|
|
|
|||
|
|
|||
неизвестно |
|
|
для двусторонней области |
|
|
для односторонней области |
|||
|
для односторонней области |
|||
генеральной дисперсии с утверждением |
|
|
|
|
|
|
|||
|
|
|||
генеральной доли признака с утверждением |
достаточно большие п,
|
|
|
,
|
|
,
|
|||
|
,
|
,
,
,
,
,
,
неизвестно
,
,
,
−
аргумент функции Лапласа;
−
распределение Стьюдента;
−
распределение Пирсона
2) Проверка гипотез для двух независимых выборок
Сравнение |
|
Статистика критерия |
|
Область принятия
|
генеральных средних
|
известны |
|
|
,
|
|
,
|
|||
|
,
|
|||
и неизвестны, но равны |
Если
принимается
|
|
,
для двусторонней области |
|
|
,
для односторонней области |
|||
|
,
для односторонней области |
|||
генеральных дисперсий |
неизвестны |
Если принимается
|
|
|
|
,
|
|||
генеральных долей признака |
достаточно большие |
|
|
,
|
|
,
|
|||
|
,
|
и
,
,
то генеральная средняя оценивается
величиной:
и
,
то генеральная дисперсии оценивается
величиной:
,
и
,
,
− аргумент функции Лапласа; − распределение Стьюдента;
− распределение Фишера–Снедекора.
3. Построение теоретического закона распределения св по опытным данным
Пусть на основе статистических данных был сделан выбор теоретического закона распределения СВ. Для частных случаев распределения закон содержит параметры, которые имеют в качестве своих оценок выборочное среднее и исправленное среднее квадратическое отклонение.
Дискретная св
Произведено
опытов. Каждый опыт состоит из
независимых испытаний, в каждом из
которых вероятность
появления события А постоянна.
Дискретная СВ
–
«число появлений события А»
описывается рядом:
-
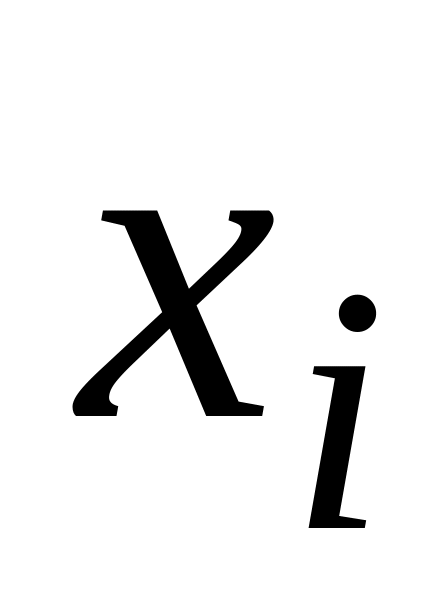
0
1
…
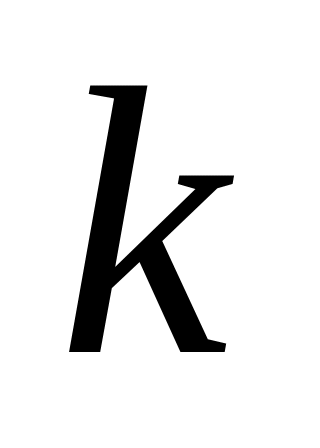
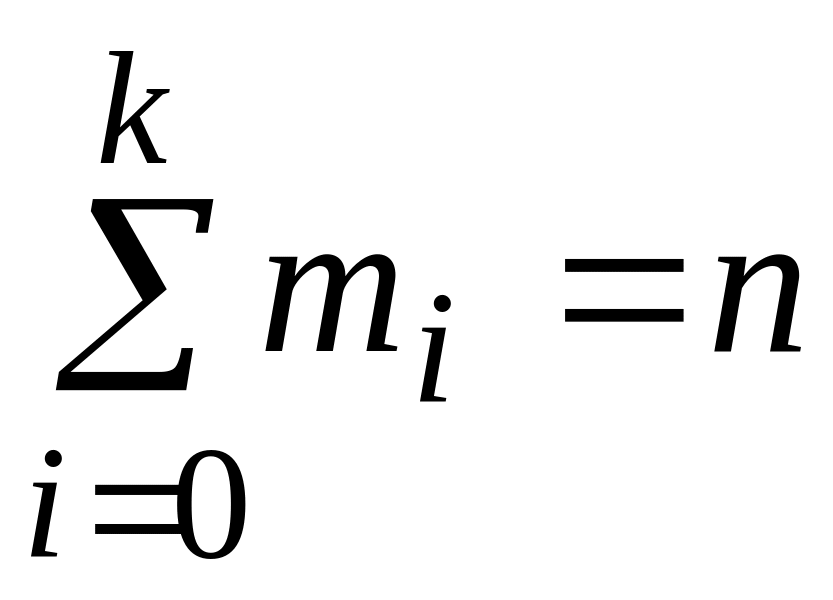
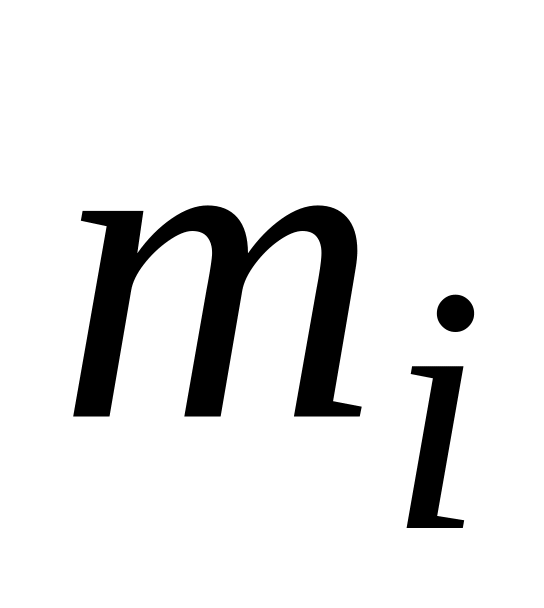
Биномиальный закон распределения |
– невелико |
|
– велико |
|
|
|
||
Закон распределения Пуассона |
– велико |
|
|
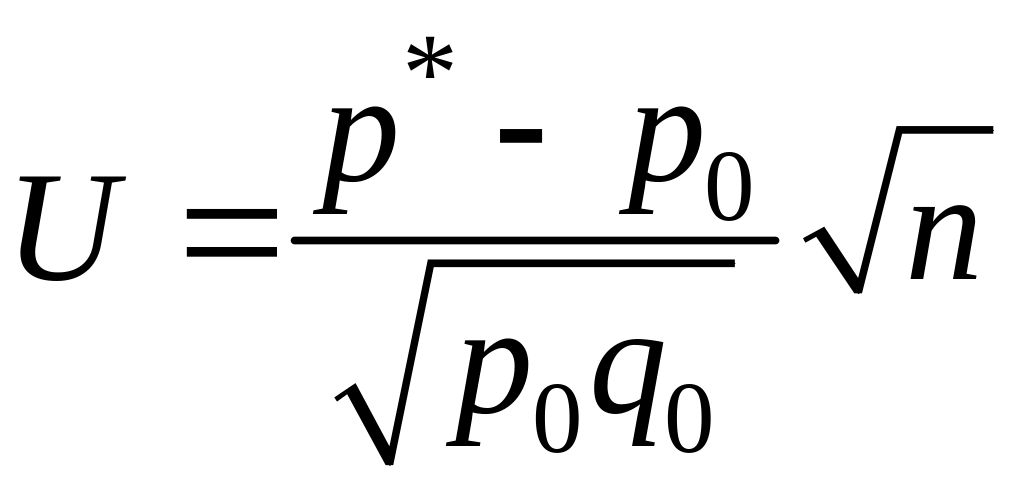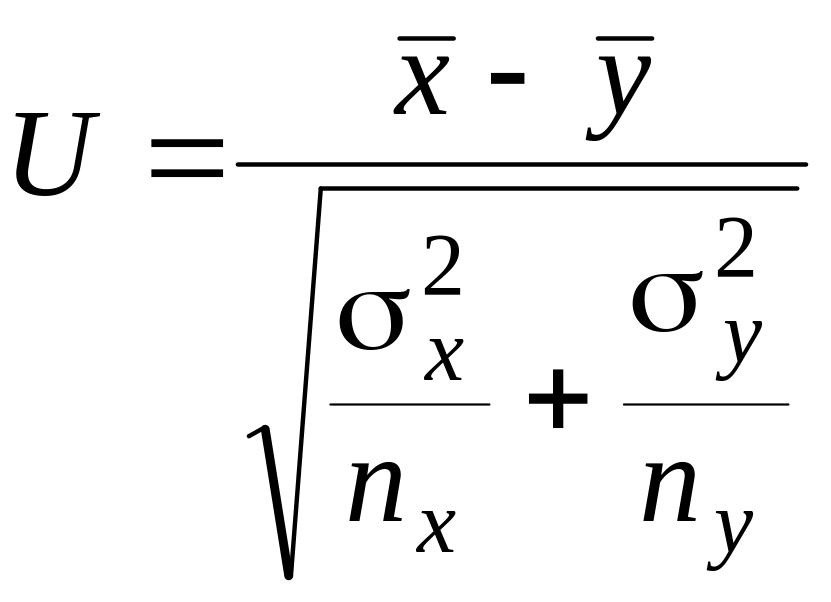
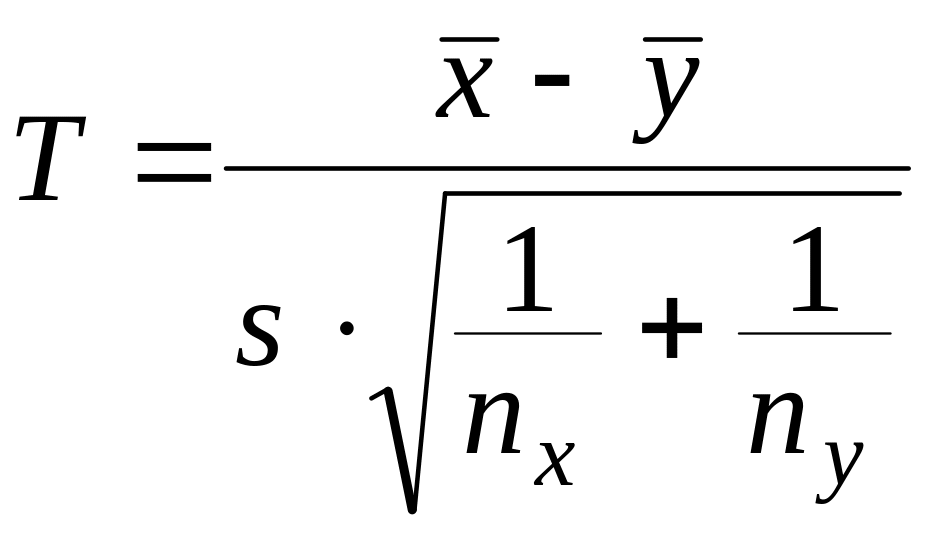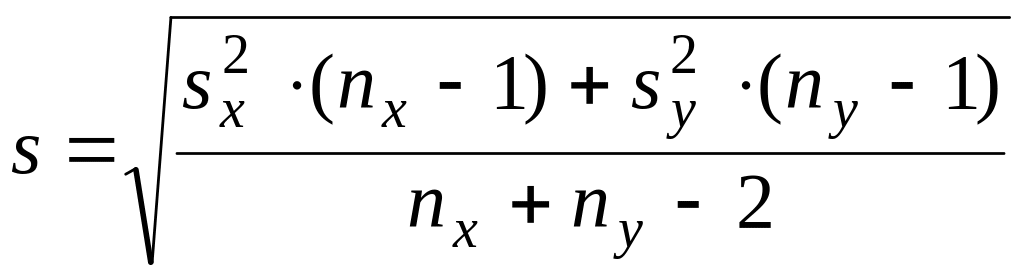
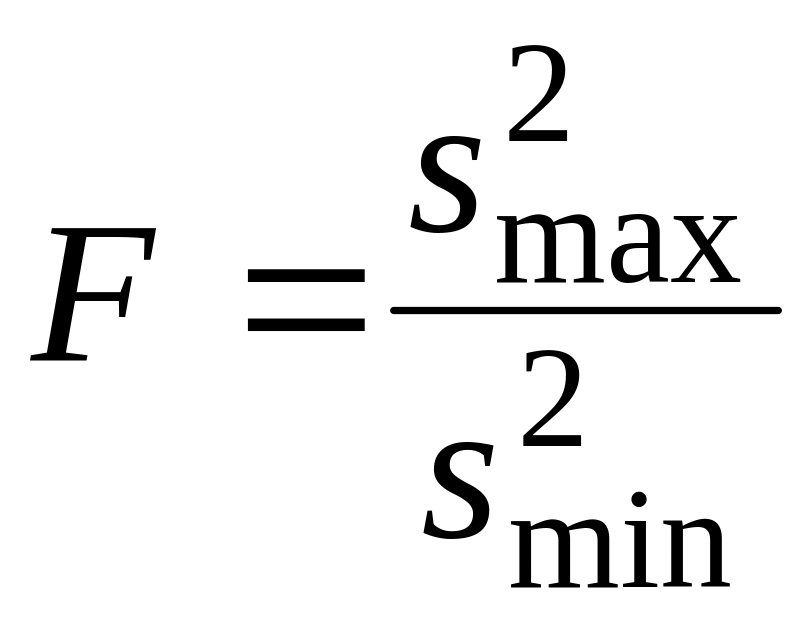
