4. Вычисление выборочных средней и дисперсии при больших (очень малых) значениях вариант
Так как выборочное среднее, выборочная дисперсия являются статистическими аналогами математического ожидания и дисперсии теоретического распределения, то справедливы следующие свойства:
Если варианты увеличить (уменьшить) на число
,
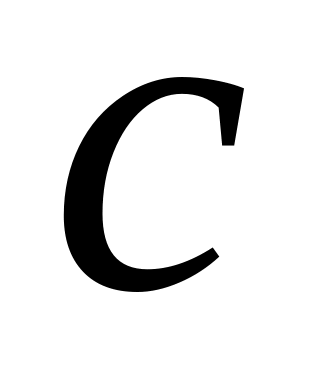то выборочное среднее также увеличится
(уменьшится) на число
,
а выборочная дисперсия останется без
изменений:
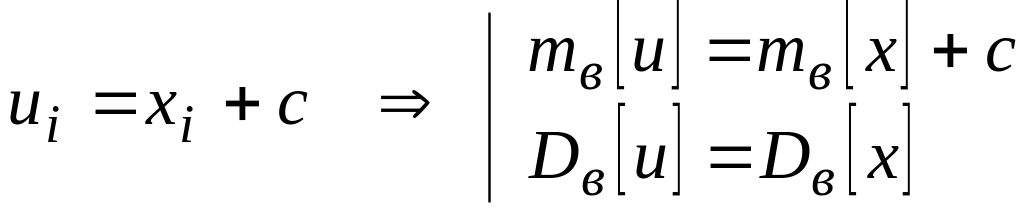
Если варианты увеличить (уменьшить) в
раз, то выборочное среднее также
увеличится (уменьшится) в
раз, а выборочная дисперсия увеличится
(уменьшится) в
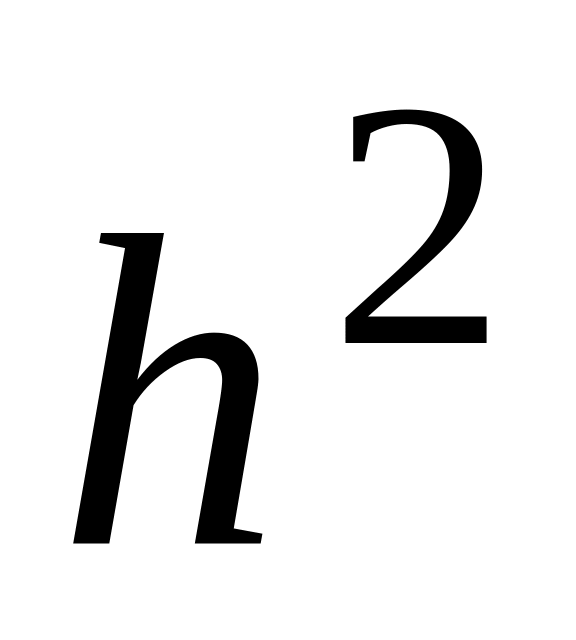раз:
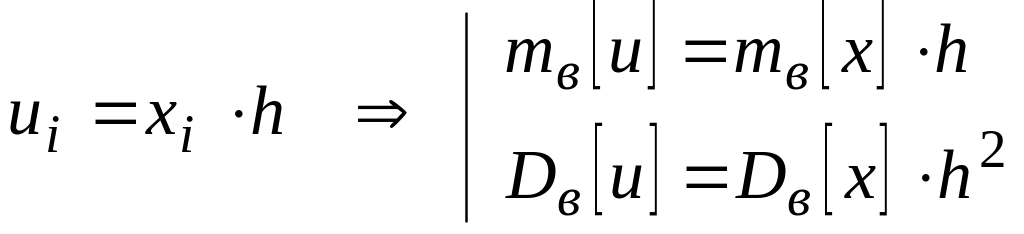
Из свойств вытекает метод упрощённых вычислений:
Вводят новую варианту
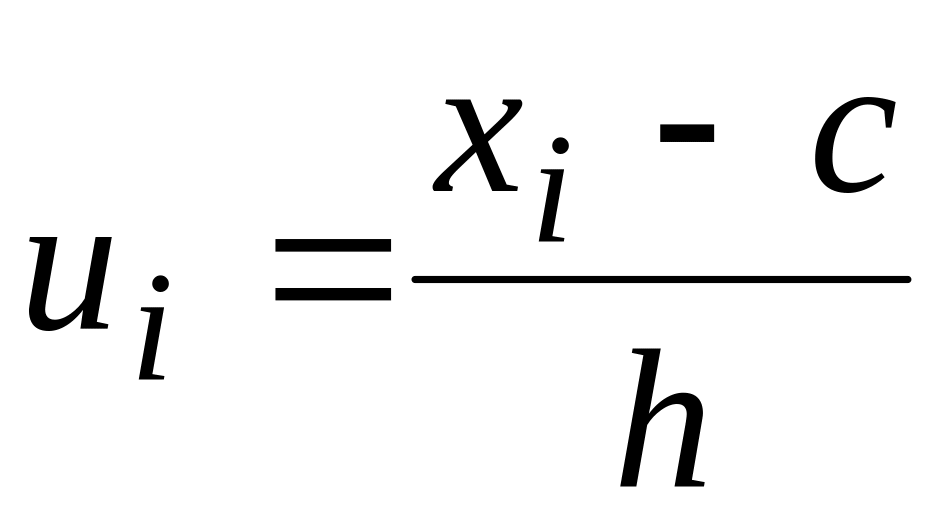.Для новой варианты просчитывают выборочные начальные моменты:
;
.
Определяют выборочные характеристики исходной совокупности:
и
.
.
.
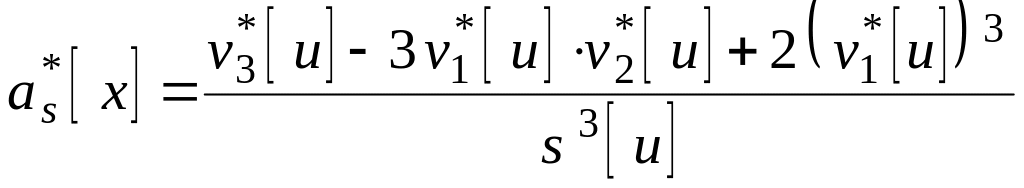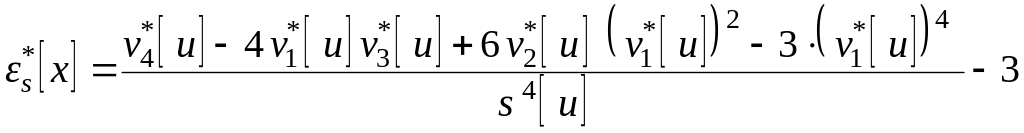§2. Оценка параметров распределения
ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ.
Во всяком статистическом распределении число опытов ограничено, что определяет случайный негладкий вид функциональных закономерностей (полигон, гистограмма, кумулята). Необходимо подобрать для данного статистического распределения аналитическую формулу, выражающую лишь существенные черты статистического материала. Такая задача называется задачей выравнивания статистического материала.
Обычно выравниванию подвергаются
гистограммы. Принципиальный вид
выравнивающей плавной кривой
выбирается исходя из условий возникновения
СВ X и из соображений,
связанных с внешним видом гистограммы.
В общих случаях, когда зависимость
линейная
,
квадратичная
,…,
неизвестные параметры
ищут методом наименьших квадратов. При
этом аналитическая функция
должна обладать основными свойствами
плотности распределения:
.
Если предполагается, что распределение
носит характер частных случаев
распределения (биномиальное, нормальное,
показательное, равномерное), то параметры
выбираются так, чтобы важнейшие моменты
(математическое ожидание, дисперсия)
статистического и выравнивающего
распределений совпадали.
§2.1 Точечные оценки параметров распределения генеральной совокупности
1. Понятие точечной оценки параметров
Пусть должно произойти n независимых опытов.
Обозначим
значение, которое примет СВ
в i–ом опыте.
также будет являться СВ, имеющей тот же
закон распределения, что и сама СВ
.
Пусть по результатам n
опытов необходимо определить (приближённо)
некоторый параметр
,
связанный с законом распределения СВ
генеральной совокупности.
Приближённое значение параметра
назовём его оценкой
.
Любая оценка, вычисляемая на основе
выборки, есть функция СВ
,
и, значит, сама является случайной
величиной. Если число наблюдений (опытов)
сравнительно невелико, то замена
неизвестного параметра
его оценкой
,
например, математического ожидания
выборочным средним, приводит к ошибке.
Эта ошибка в среднем тем больше, чем
меньше число опытов.
Для того, чтобы оценка неизвестного параметра давала хорошее приближение, она должна удовлетворять следующим требованиям:
Несмещённость.
Состоятельность.
Эффективность.
Оценка называется несмещённой, если математическое ожидание оценки параметра по всевозможным выборкам данного объёма равно истинному значению определяемого параметра:
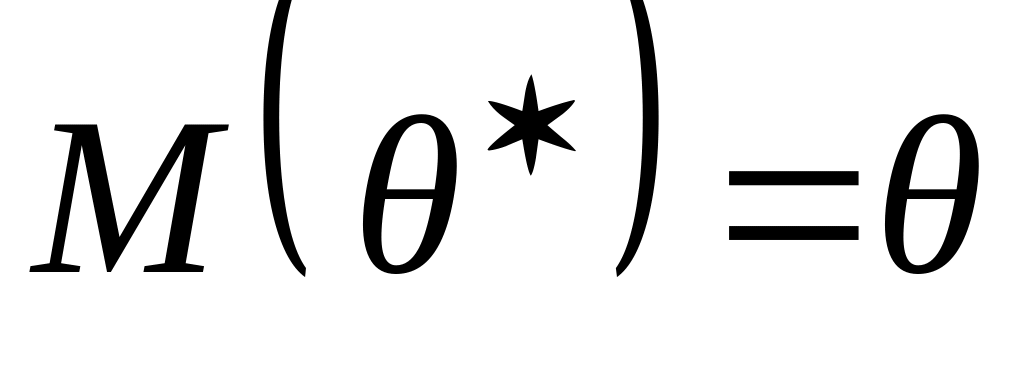.Оценка называется состоятельной, если при увеличении объёма выборки оценка сходится по вероятности к истинному значению параметра:
или
,
где
–
сколь угодно малое положительное число.
Из неравенства Чебышева следует, что
для удовлетворения этого требования
достаточно, чтобы оценка была несмещённой
и
.
Оценка называется эффективной, если
.
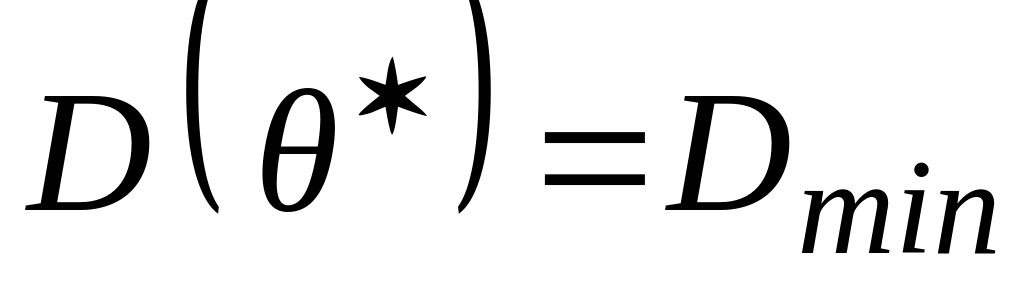