
- •Тема «Числовые и функциональные ряды. Ряд Тейлора»
- •1 (1).Исследовать на сходимость ряд
- •(4)Определить сходимость ряда .
- •(1).Исследовать на сходимость ряд
- •Тема «Комплексные числа и теория функции комплексного переменного»
- •7.Изобразить область, ограниченную линиями:
- •8. Найти изображение следующих функций-оригиналов, используя теоремы операционного исчисления и таблицу.
- •9.Найти оригинал для изображения при помощи разложения на простейшие дроби.
- •Действия над комплексными числами
Тема «Числовые и функциональные ряды. Ряд Тейлора»
1 (1).Исследовать на сходимость ряд
Решение.
Используем
I
признак сравнения. Так как
![]() ,
а гармонический ряд
,
а гармонический ряд
![]() расходится, то расходится и ряд
расходится, то расходится и ряд
![]() .
.
(2)Исследовать на сходимость ряд
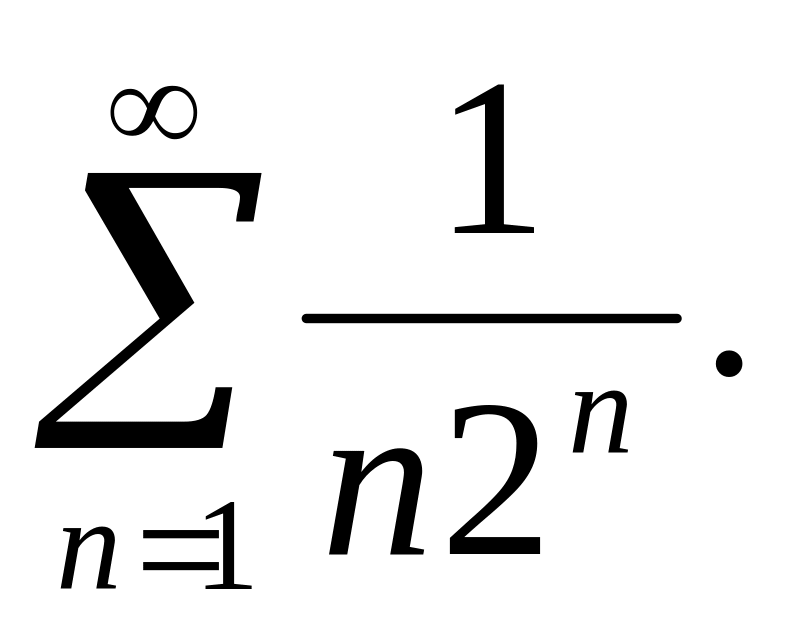
Решение.
Используем
I
признак сравнения. Так как
![]() ,
а ряд
,
а ряд
![]() сходится (как убывающая геометрическая
прогрессия), то ряд
сходится (как убывающая геометрическая
прогрессия), то ряд
![]() тоже сходится.
тоже сходится.
(3)Исследовать на сходимость ряд
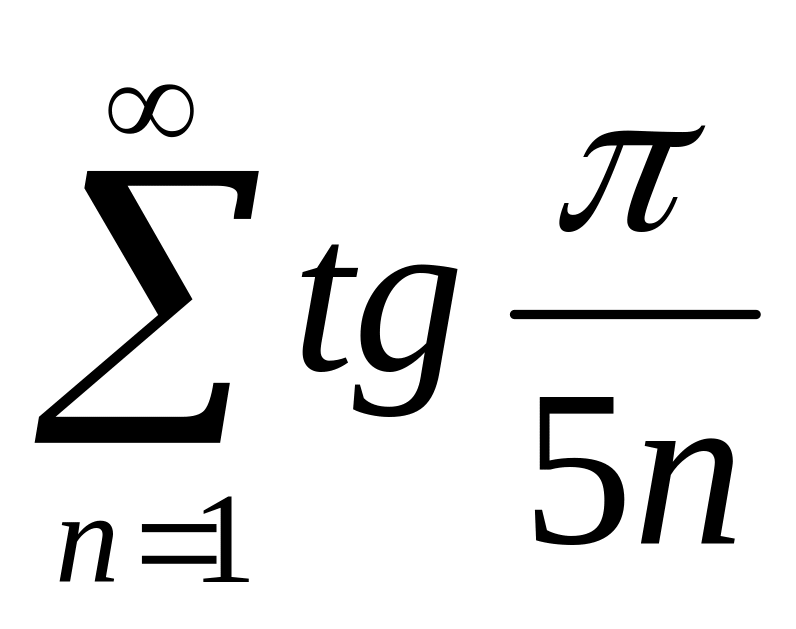 .
.
Решение.
Применим
предельный признак сравнения, возьмем
![]() ,
который расходится, так как является
гармоническим рядом. Тогда
,
который расходится, так как является
гармоническим рядом. Тогда
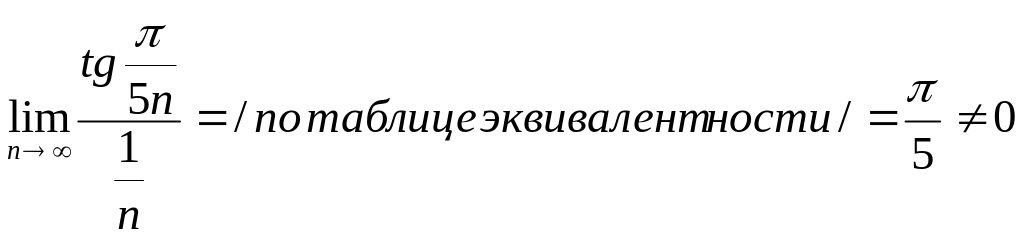 ,
следовательно, ряд расходится.
,
следовательно, ряд расходится.
(4)Определить сходимость ряда .
Решение.
Используем
признак Даламбера. Для этого определим
![]() .
.
Тогда
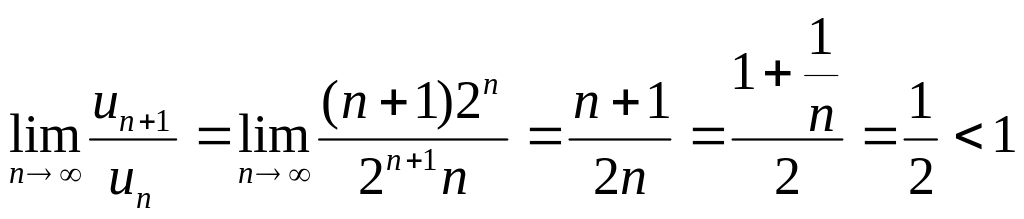 ,
следовательно, ряд сходится.
,
следовательно, ряд сходится.
(5) Определить сходимость ряда
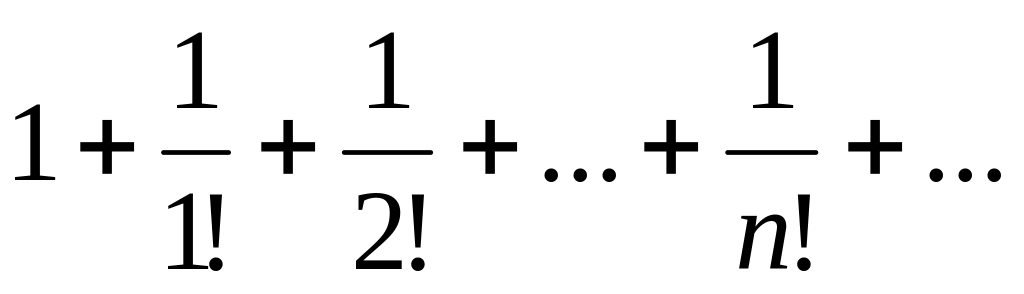
Решение.
Используем
признак Даламбера. Для этого определим
![]() .
.
Тогда
![]() ,
следовательно, ряд сходится.
,
следовательно, ряд сходится.
(6) Определить сходимость ряда
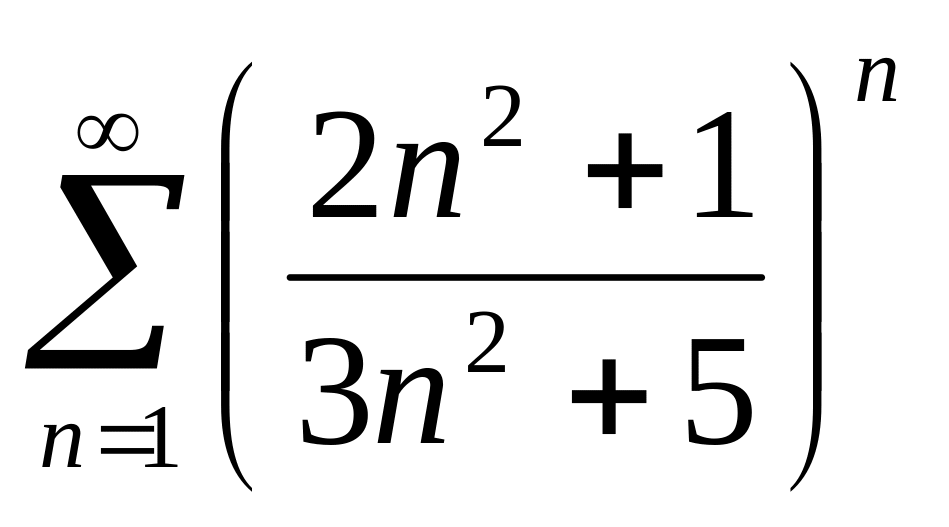 .
.
Решение.
Используем
радикальный признак Коши. Для этого
определим
![]() .
Тогда
.
Тогда
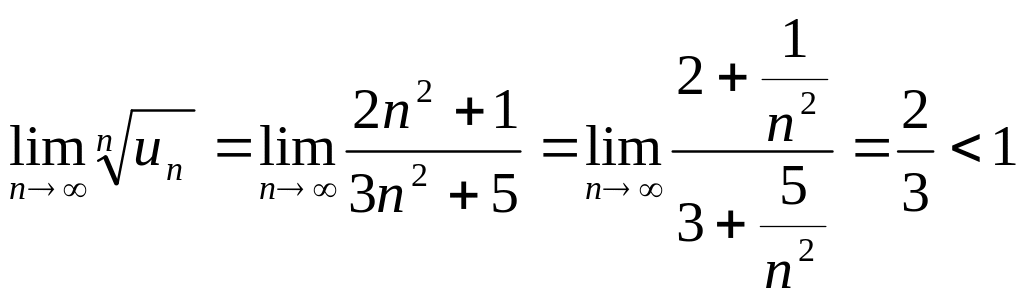 ,
следовательно, ряд сходится.
,
следовательно, ряд сходится.
(7) .Определить сходимость ряда
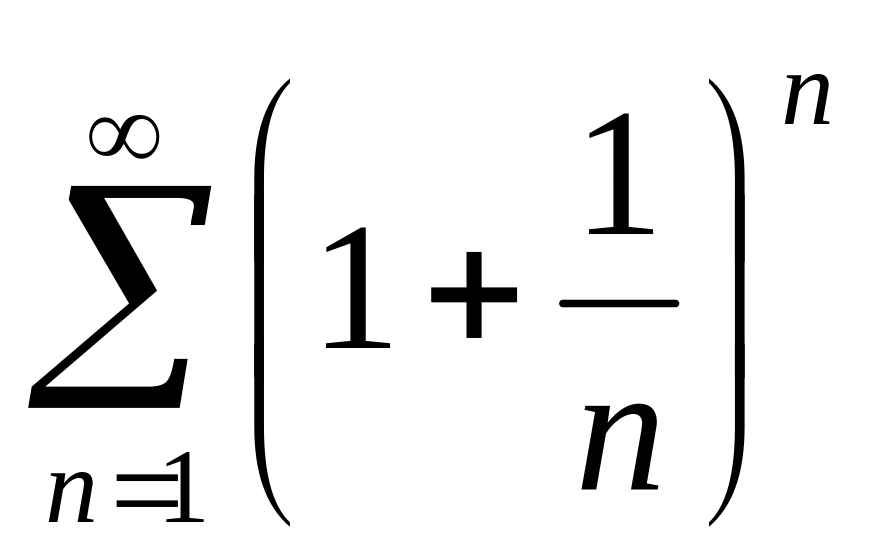 .
.
Решение.
Используем
радикальный признак Коши. Для этого
![]() Тогда
Тогда
![]() Таким образом, радикальный признак Коши
не дает ответа на вопрос о сходимости
ряда. Проверим выполнение необходимого
условия сходимости:
Таким образом, радикальный признак Коши
не дает ответа на вопрос о сходимости
ряда. Проверим выполнение необходимого
условия сходимости:
![]() ,
следовательно, необходимое условие
сходимости не выполняется, значит, ряд
расходится.
,
следовательно, необходимое условие
сходимости не выполняется, значит, ряд
расходится.
(8). Исследовать на сходимость ряд
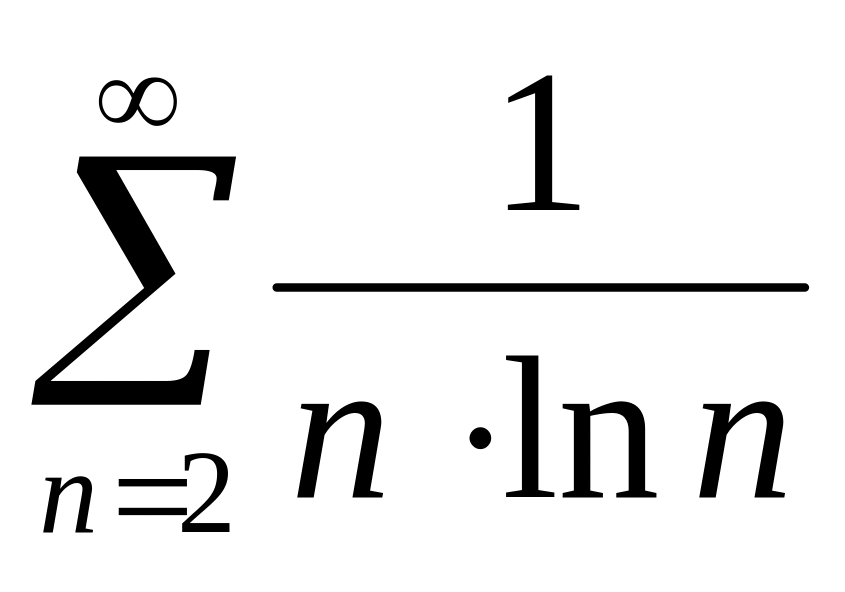 .
.
Решение.
Используем интегральный признак Коши.
![]() ,
следовательно, ряд расходится.
,
следовательно, ряд расходится.
(9) .Исследовать на сходимость ряд
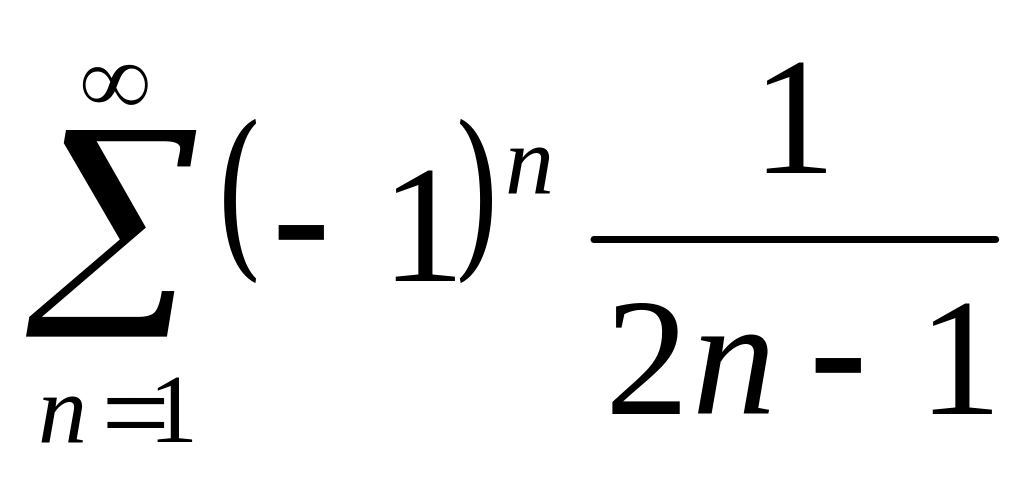 .
.
Решение.
Дан знакочередующийся ряд. Выясним, сходится ли данный ряд, применяя признак Лейбница:
1)
проверим, выполняется ли неравенство
![]() для абсолютных величин членов ряда.
для абсолютных величин членов ряда.
![]() ,
следовательно, неравенство выполняется.
,
следовательно, неравенство выполняется.
2)
найдем предел общего члена ряда:
![]() ,
следовательно, условие выполнено.
,
следовательно, условие выполнено.
Значит, по признаку Лейбница, исходный ряд сходится.
Исследуем
на сходимость ряд из абсолютных величин
членов данного ряда:
![]() .
Возьмем гармонический ряд
.
Возьмем гармонический ряд
![]() ,
который расходится, и используем 2
признак сравнения:
,
который расходится, и используем 2
признак сравнения:
![]() .
Следовательно, ряд из абсолютных величин
расходится.
.
Следовательно, ряд из абсолютных величин
расходится.
Таким образом, получаем, что исходный знакочередующийся ряд сходится условно.
(1).Исследовать на сходимость ряд
Решение.
Найдем радиус сходимости, применяя признак Даламбера:
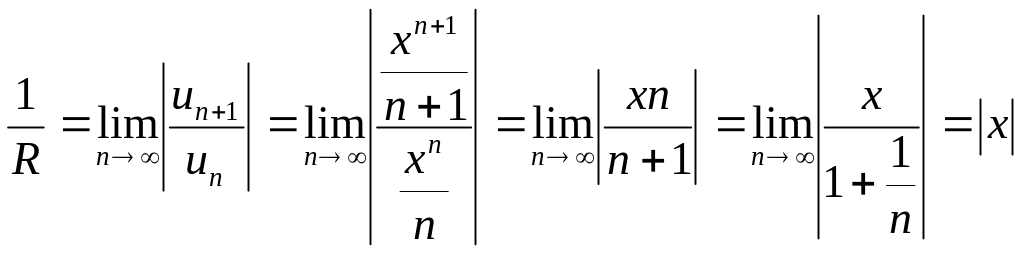 .
.
Получаем,
что этот ряд сходится при
![]() и
расходится при
и
расходится при
![]() ,
получаем интервал сходимость: -1<x<1.
,
получаем интервал сходимость: -1<x<1.
Рассмотрим ряд на границах полученного интервала.
При
х = -1:
![]() ряд сходится по признаку Лейбница.
ряд сходится по признаку Лейбница.
При
х = 1:
![]() ряд расходится (гармонический ряд).
ряд расходится (гармонический ряд).
Таким
образом, ряд сходится при
![]() .
.
(2)Найти область сходимости ряда
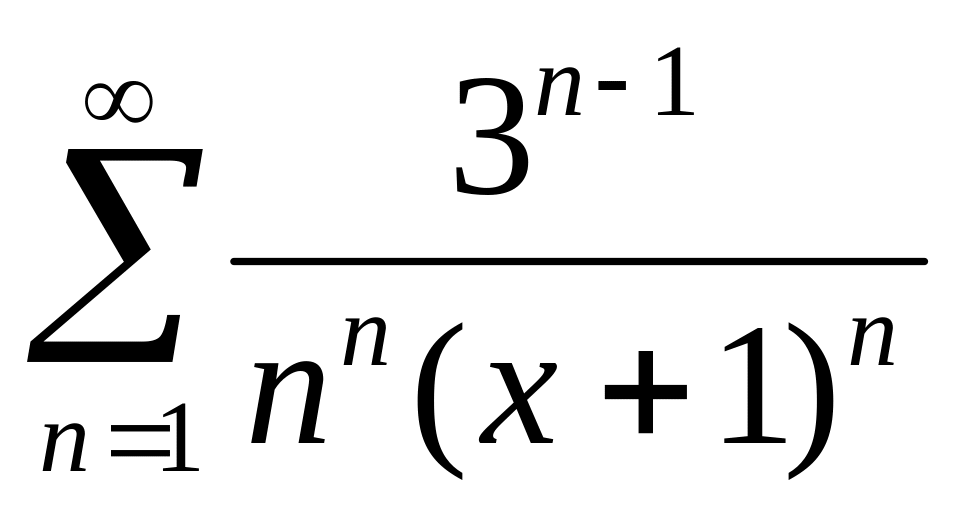 .
.
Решение.
Найдем радиус сходимости, применяя обратный признак Коши::
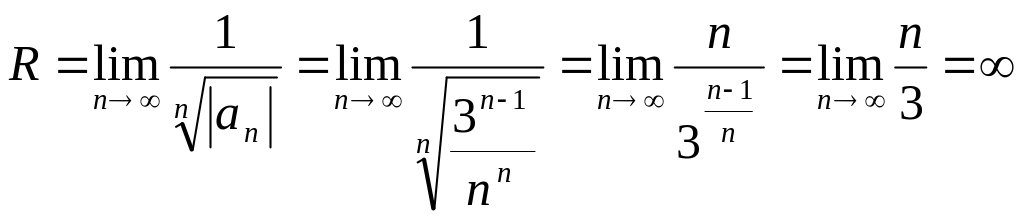 .
.
Получаем,
что ряд сходится при
![]() ,
следовательно,
,
следовательно,
![]() .
.
Таким
образом, ряд сходится в одной точке
![]() .
.
3.
Найти область сходимости ряда
![]()
Найдем радиус сходимости, применяя обратный признак Даламбера:
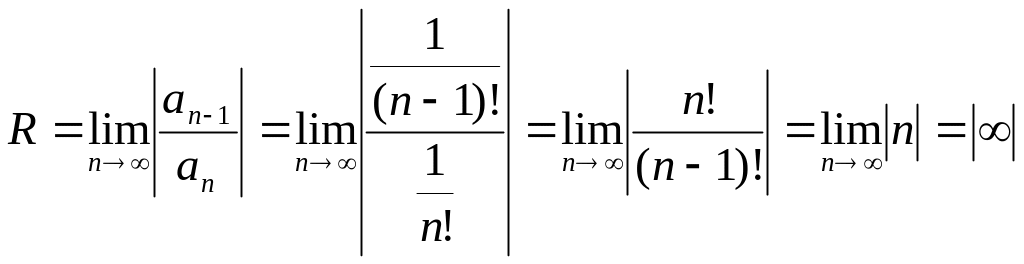 .
.
Следовательно, данный ряд сходится при любом значении х, так как общий член этого ряда стремится к нулю.
(1).Разложить в ряд Маклорена функцию
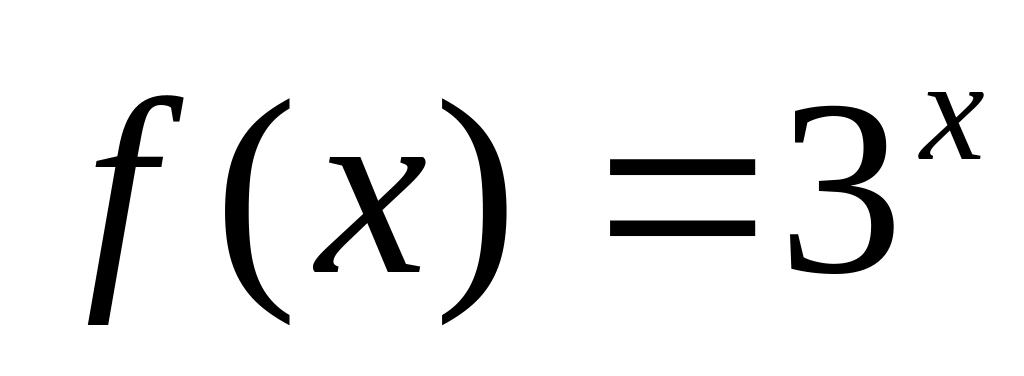 .
.
Решение.
Так
как
![]() .
Получаем:
.
Получаем:
![]()
(2) Разложить в ряд Маклорена функцию
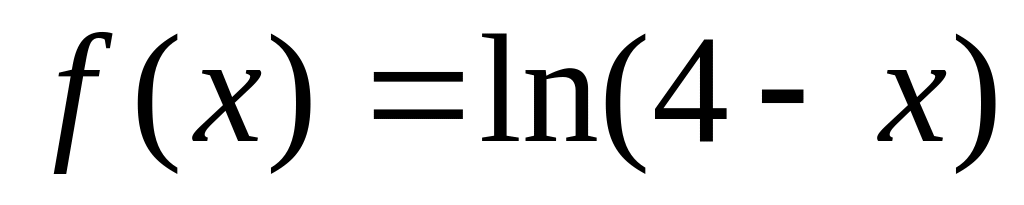 .
.
Решение.
Так
как
![]() ,
то
,
то
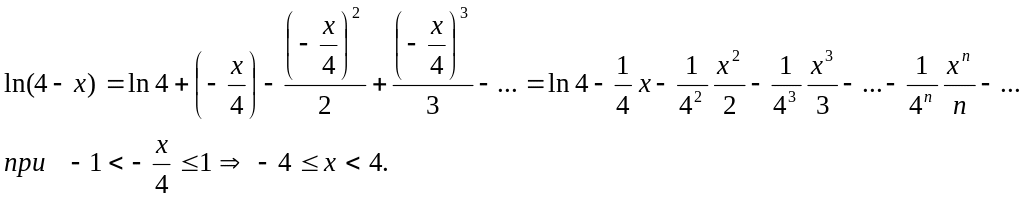
3(3)
.Разложить в ряд Маклорена функцию![]() .
.
Решение.
Так
как
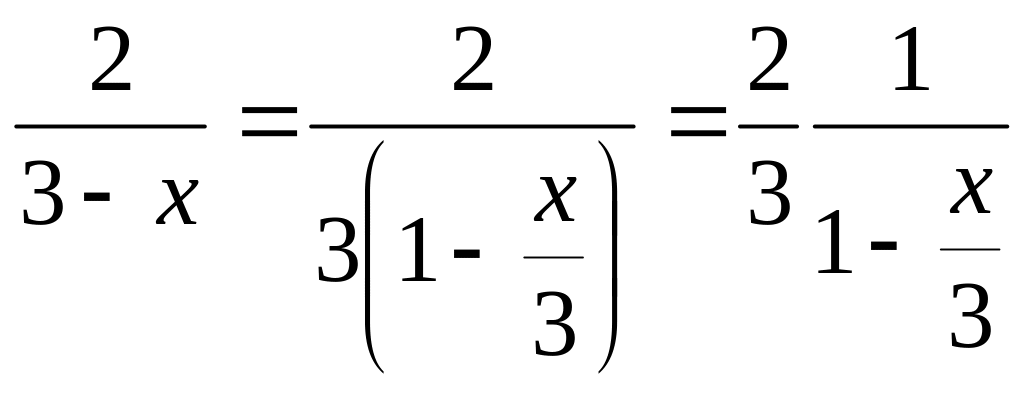 ,
заменив х на
,
заменив х на
![]() ,
получаем
,
получаем
![]() .
.
