Вариант 9 Тема «Числовые и функциональные ряды. Ряд Тейлора»
Определить сходимость числового ряда
Найти область сходимости функционального ряда:
Разложить функцию в ряд Маклорена: (1)
(2)
по степеням
Тема «Комплексные числа и теория функции комплексного переменного»
Вычислить и записать в алгебраической форме
.Решить уравнение:
Вычислить и записать в тригонометрической форме
Изобразить область, ограниченную линиями:
Тема «Операционное исчисление»
8 Используя теоремы линейности ,смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a)
;
б)
.
9 Найти оригинал по заданному изображению:
.
Тема «Теория вероятностей и математическая статистика».
Произведено два выстрела по цели. Вероятность попадания при каждом выстреле равна 0.7. Цель поражается с одного попадания с вероятностью 0.5, при двух попаданиях – с вероятностью 0.9. Найти вероятность: 1) поражения цели при двух выстрелах; 2) того, что оба снаряда попали в цель, если окажется, что цель поражена.
На каждом станке за смену выпускается п деталей. Вероятность брака для первого станка равна р1, для второго – р2. Найти вероятность р того, что в сменной продукции обоих станков не более одной бракованной детали. Вычислить эту вероятность при: 1) n = 8, p1 = 0.05, p2 = 0.03; 2) n =100, p1 = 0.005, p2 = 0.003 по формуле Пуассона.
СВ задана законом распределения. Найти: 1) числовые характеристики , ; 2) функцию распределения и построить ее график; 3)вероятность , 4) закон распределения величины СВ
.
Вычислить
,
дважды, используя свойства (по результатам
предыдущих пунктов) и непосредственно
составленный закон распределения.
-
20
30
40
50
60
0,2
0,1
0,2
0,4
?
13.
Дана плотность вероятности f(x)
случайной величины X:
Найти: 1) С;
2) F(x);
3) mX
;
4) DX
; 5) (x);
6) Р(X
<
2); 7) построить
график f(x)
и F(x).
14. задание по мат.статистике см. в конце
Вариант 0 Тема «Числовые и функциональные ряды. Ряд Тейлора»
Определить сходимость числового ряда
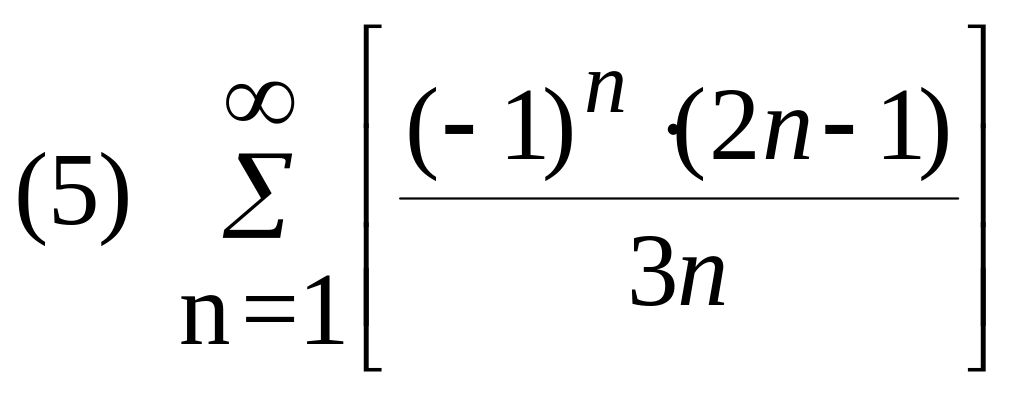
Найти область сходимости функционального ряда:
Разложить функцию в ряд Маклорена: (1)
(2)
по степеням
Тема «Комплексные числа и теория функции комплексного переменного»
Вычислить и записать в алгебраической форме
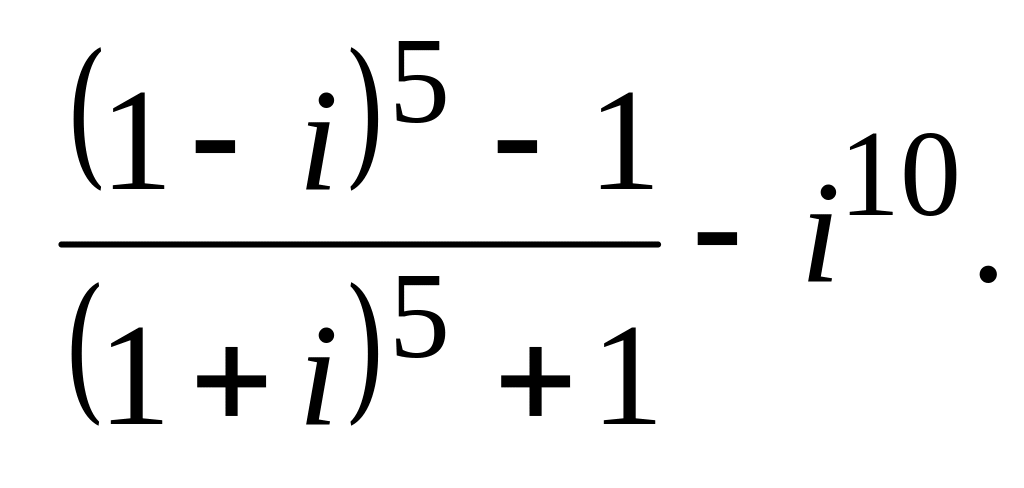.Решить уравнение:
Вычислить и записать в тригонометрической форме
Изобразить область, ограниченную линиями:
Тема «Операционное исчисление»
8 Используя теоремы линейности ,смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a)
;
б)
.
9 Найти оригинал по заданному изображению:
.
Тема «Теория вероятностей и математическая статистика».
На любой из позиций импульсного кода могут быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс). Помехами «1» преобразуется в «0» с вероятностью 0.02 и «0» в «1» с вероятностью 0.04. Найти вероятность: 1) приема «0» на конкретной позиции кода; 2) того, что был передан «0», если принят «0».
В первой партии – 100 деталей. Вероятность брака в этой партии – 0.01. Во второй партии – 200 деталей, вероятность брака – 0.005. Найти вероятность того, что в обеих партиях нет бракованных деталей. Вычислить: 1) эту вероятность по формуле Бернулли; 2) ту же вероятность с помощью формулы Пуассона.
12. СВ задана законом распределения. Найти: 1) числовые характеристики , ; 2) функцию распределения и построить ее график; 3)вероятность , 4) закон распределения величины СВ . Вычислить , дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно составленный закон распределения.
-
30
40
50
60
70
?
0,1
0,2
0,4
0,1
13.
Дана плотность вероятности f(x)
НСВ X:
Найти: 1) С;
2) F(x);
3) mX;
4) DX;
5) (x);
6)
;
7) построить график f(x)
и F(x).