Тема «Числовые и функциональные ряды. Ряд Тейлора»
Определить сходимость числового ряда
Найти область сходимости функционального ряда:
Разложить функцию в ряд Маклорена: (1)
(2)
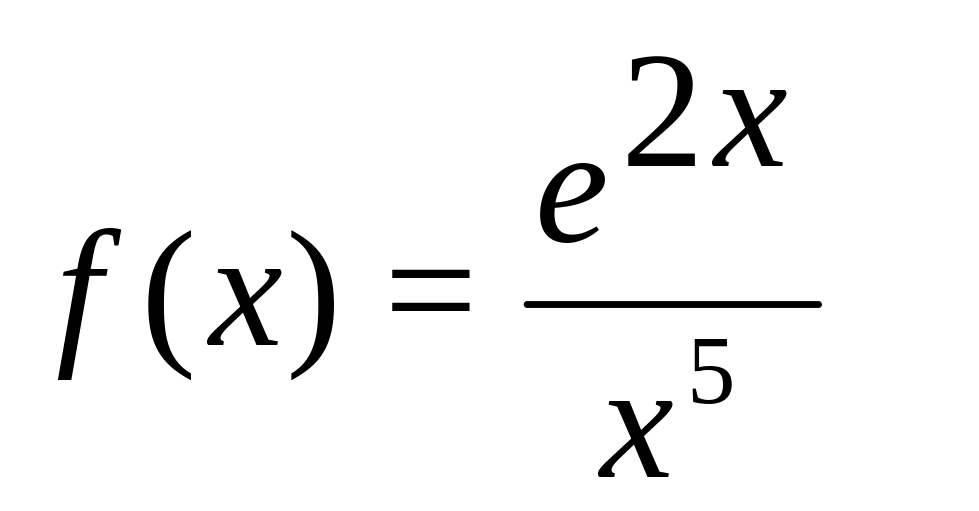по степеням
Тема «Комплексные числа и теория функции комплексного переменного»
Вычислить и записать в алгебраической форме
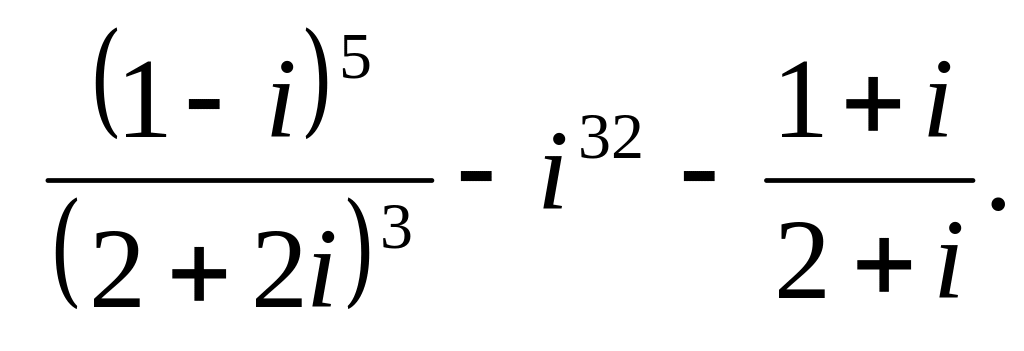.Решить уравнение:
Вычислить и записать в тригонометрической форме
Изобразить область, ограниченную линиями:
Тема «Операционное исчисление»
8 Используя теоремы линейности ,смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a)
;
б)
.
9 Найти оригинал по заданному изображению:
.
Тема «Теория вероятностей и математическая статистика».
Прибор содержит два независимо работающих блока. Исправность каждого из них необходима для работы прибора. Вероятность отказа блоков за время Т: для первого – p1=0.1, для второго – p2 = 0.2. Прибор испытывался в течение времени Т и вышел из строя. Найти: 1) вероятность Р (А) отказа прибора за время Т; 2) вероятность того, что при отказе прибора за время Т отказал только первый блок.
По каналу связи посылаются n сообщений. Помехами каждое сообщение может быть искажено с вероятностью p. Найти: 1) каким должно быть n, чтобы хотя бы одно сообщение дошло не искаженным до адресата с вероятностью не меньшей 0.99 при p =0.3; 2) вероятность искажения не более одного сообщения при n =100, p =0.02 (с помощью формулы Пуассона).
СВ задана законом распределения. Найти: 1) числовые характеристики , ; 2) функцию распределения и построить ее график; 3)вероятность
,
4) закон распределения величины СВ
.
Вычислить
,
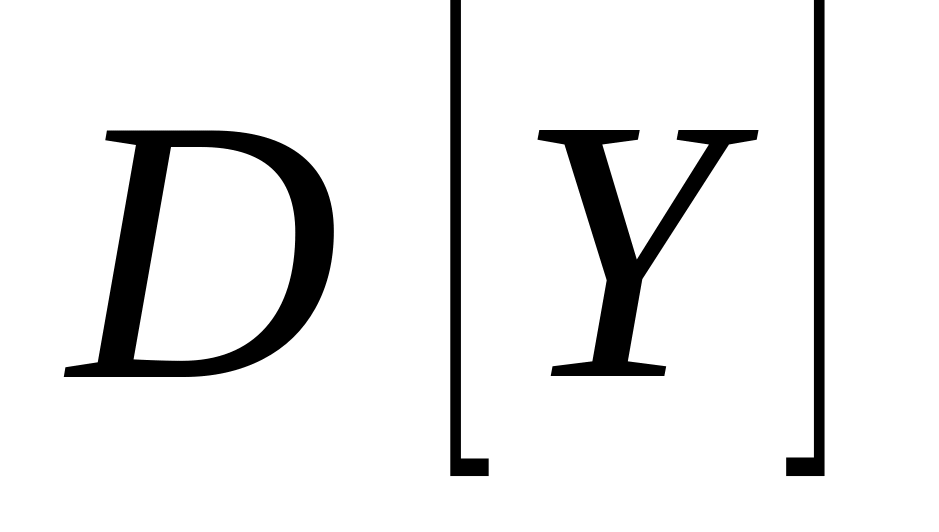дважды, используя свойства (по результатам
предыдущих пунктов) и непосредственно
составленный закон распределения.
-
40
50
60
70
80
?
0,2
0,1
0,2
0,4
13.
Дана плотность вероятности f(x)
непрерывной случайной величины X:
Найти: 1) С;
2) F(x);
3) mX
;
4) DX
; 5) (x);
6) Р(X
<
1); 7) построить
график f(x)
и F(x).
14. задание по мат.статистике см. в конце
Вариант 6 Тема «Числовые и функциональные ряды. Ряд Тейлора»
Определить сходимость числового ряда
Найти область сходимости функционального ряда:
Разложить функцию в ряд Маклорена: (1)
(2)
по степеням
Тема «Комплексные числа и теория функции комплексного переменного»
Вычислить и записать в алгебраической форме
.Решить уравнение:
Вычислить и записать в тригонометрической форме
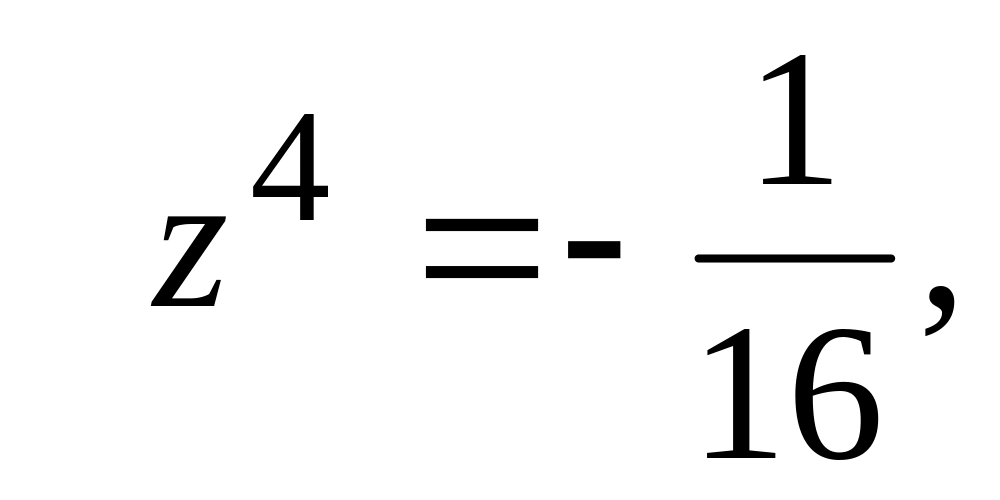
Изобразить область, ограниченную линиями:
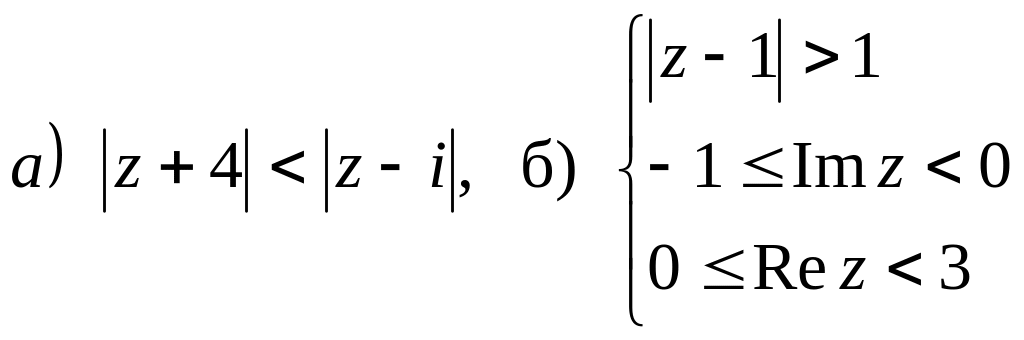
Тема «Операционное исчисление»
8 Используя теоремы линейности ,смещения и запаздывания и таблицу оригиналов и изображений найти изображения для данных оригиналов:
a)
;
б)
.
9 Найти оригинал по заданному изображению:
.
Тема «Теория вероятностей и математическая статистика».
Партия резисторов изготовлена двумя заводами, причем продукции первого завода в 2 раза больше, чем второго. Вероятность брака на первом заводе равна 0.04, на втором – 0.06. Найти вероятность того, что случайным образом взятая деталь партии: 1) оказалась бракованной; 2) изготовлена первым заводом, если при проверке она оказалась бракованной.
За период в 131 год с 1865 по 1995 г. в Санкт-Петербурге 10-го января (рождественские морозы) мягкая зимняя погода со среднесуточной температурой от минус 5 до 0 (событие А) наблюдалась 35 раз, а не ниже минус +2 (событие В) – всего 5 раз. Исходя из этих статистических данных, примем Р(А)=35/131=0.27, Р(В)=5/131=0.04. Найти вероятность: 1) того, что в предстоящие ближайшие 4 года событие А будет наблюдаться не менее двух раз; 2) появления события В хотя бы один раз в предстоящие 20 последовательных лет с помощью формулы Пуассона.
СВ задана законом распределения. Найти: 1) числовые характеристики , ; 2) функцию распределения и построить ее график; 3)вероятность , 4) закон распределения величины СВ
.
Вычислить
,
дважды, используя свойства (по результатам
предыдущих пунктов) и непосредственно
составленный закон распределения.
-
50
60
70
80
90
0,1
?
0,1
0,2
0,4
13.
Дана плотность вероятности f(x)
НСВ X:
Найти: 1) С;
2) F(x);
3) mX;
4) DX;
5) (x);
6)
;
7) построить график f(x)
и F(x).
14. задание по мат.статистике см. в конце