Міністерство освіти і науки України

Національний університет водного господарства та природокористування

Кафедра прикладної математики

100-97

Методичні вказівки

до виконання практичних робіт з дисципліни «Функціональний аналіз »

для студентів напряму 6.040301

«Прикладна математика»

денної форми навчання

Частина 1

Рекомендовані до видання методичною комісією напряму «Прикладна математика»

Протокол №3 від 11 січня 2010 р.

Рівне -2010

Методичні вказівки до виконання практичних робіт з дисципліни «Функціональний аналіз» для студентів напряму 6.040301 «Прикладна математика» денної форми навчання. Частина 1/ Гладун Л.В. – Рівне: НУВГП, 2010. - 28 с.

Упорядник: Л.В. Гладун, к.ф.-м.н., доцент кафедри прикладної математики

Відповідальний за випуск: А.П. Власюк, д. т. н., професор, завідувач кафедри прикладної математики

© Гладун Л.В., 2010

© НУВГП, 2010

ЗМІСТ

Вступ 3

1. Метричні простори 4

2. Нормовані простори 16

3. Література 27 Вступ

Функціональний аналіз відіграє важливу роль у сучасній математичній освіті спеціаліста із прикладної математики, якому потрібно використовувати математичні методи при розв’язанні конкретних задач.

Методичні вказівки розроблені для студентів напряму “Прикладна математика” . Вони також можуть використовуватись для студентів технічних вузів, а також для студентів фізико-математичних напрямів педагогічних вузів.

В першій практичній роботі розглянуто поняття метрики, а також принцип стискуючих відображень у повних метричних просторах.

Друга практична робота, крім поняття норми на лінійному просторі, містить узагальнення поняття збіжності числової послідовності.

До кожної практичної роботи приводиться необхідний теоретичний матеріал. Також наведено приклади розв’язання найбільш типових задач.

В кінці кожної практичної роботи подано завдання для самостійної роботи, що містять значну кількість задач. Вони можуть використовуватися для проведення тестового опитування з відповідних тем.

Задачі, номери яких більші за тридцять, можна віднести до задач підвищеної складності.

Практична робота №1 Метричні простори

Нехай - довільна множина, а - функція декартового добутку в множину дійсних чисел. Функція називається метрикою або відстанню на , якщо вона задовольняє наступним умовам (аксіомам) :

1)

2) (аксіома симетрії);

3) (аксіома тотожності);

4) (аксіома трикутника).

Множина , разом із заданою на неї метрикою , називається метричним простором, а число - відстанню між елементами і .

Точка називається нерухомою точкою відображення якщо

Відображення називається стискуючим, якщо існує таке число , що для довільних елементів виконується нерівність .

Теорема (принцип стискуючих відображень). Нехай - повний метричний простір. Тоді кожне стискуюче відображення має одну і тільки одну нерухому точку.

Приклад 1. Перевірити чи є функція метрикою на множині .

Розв’язування. Перша аксіома метрики має вигляд : . Згідно означення функції модуль така нерівність завжди виконується. Оскільки

, то аксіома симетрії справджується.

Запишемо аксіому тотожності : .

Необхідність. Нехай . Звідси матимемо , тобто .

Достатність. Нехай , тоді і .

Аксіома трикутника має вигляд

.

Оскільки , тоді за властивістю функції модуль отримаємо

,

тобто аксіома трикутника виконується . Отже, функція є метрикою на множині .

Приклад 2. Перевірити чи є функція метрикою на множині .

Розв’язування. Оскільки для довільних чисел завжди , то перша аксіома метрики виконується.

Аксіома симетрії

,

справджується за властивістю функції модуль.

Перевіримо аксіому тотожності

.

Необхідність. Нехай , тоді . Остання рівність може виконуватись не тільки при однакових значеннях і . Наприклад, при і маємо , тобто , але . Це означає, що аксіома тотожності не справджується. Отже, функція не є метрикою на множині .

Приклад 3. Перевірити чи є функція метрикою на множині .

Розв’язування. Значення функції дорівнює сумі невід’ємних чисел, тобто перша аксіома метрики виконується.

Аксіома симетрії

має місце так як .

Аксіома тотожності очевидна.

Нехай , - довільні елементи множини , тоді аксіома трикутника запишеться у вигляді

Оскільки

то досить довести нерівність

. (1)

Покладемо , тоді і нерівність (1) матиме вигляд

. (2)

Для доведення нерівності (2) використаємо нерівність Коші-Буняковського :

. (3)

Маємо :

,

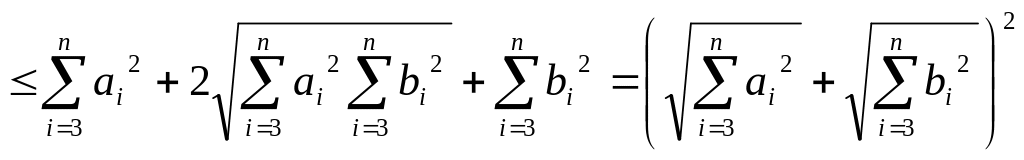тобто нерівність (2), а , значить, і нерівність (1) доведена. Отже, функція є метрикою на множині .

Приклад 4. Нехай - множина збіжних до нуля послідовностей. Перевірити чи є функція метрикою на множині .

Розв’язування. Нехай довільні елементи множини . Так як , то перша аксіома метрики виконується.

Аксіома симетрії

очевидна.

Перевіримо аксіому тотожності

.

Необхідність. Якщо , тоді отримаємо . З отриманих рівностей для елемен-тів послідовностей і не випливає обов’язкова рівність цих послідовностей. Так для послідовностей і матимемо , але . Аксіома тотожності не виконується, тобто функція не є метрикою на множині .

Приклад 5. Нехай - множина неперервних функцій на відрізку . Перевірити чи є функція метрикою на множині .

Розв’язування. Для довільних неперервних на відрізку функцій і очевидно мають місце нерівність

і рівність

,

тобто перші дві аксіоми метрики виконуються.

Аксіома тотожності має вигляд :

.

Необхідність. З рівності отримаємо . Але з цих рівностей не випливає рівність функцій і між собою, тобто що їх значення і співпадають в усіх точках відрізка . Наприклад, розглянемо функції

Ці функції не рівні між собою, але . Таким чином, функція не є метрикою на множині .

Приклад 6. Нехай - метрика на множині . Показати, що функція є також метрикою.

Розв’язування. Оскільки є метрикою на множині , то для довільних елементів та цієї множини і . Звідси випливає, що і , а, значить, і . Таким чином, функція задовольняє першій і другій аксіомам метрики.

Аксіома тотожності для функції має вигляд

.

Необхідність. Нехай , тоді , тобто . Так як метрика на множині , то за аксіомою тотожності .

Достатність. Якщо , тоді маємо : , . Отже, аксіома тотожності виконується для функції .

Перевіримо аксіому трикутника

.

Використовуючи аксіому трикутника для метрики і не-від’ємність її значень, дістанемо :

Логарифмуючи обидві частини нерівності, отримаємо :

.

Аксіома трикутника для виконується. Отже, функція є метрикою на множині .

Приклад 7. Показати , що відображення , є стискуючим на відрізку , і знайти його нерухому точку.

Розв’язування. Візьмемо довільні числа . Тоді

тобто відображення є стискуючим із коефіцієнтом .

Знайдемо його нерухому точку . Для цього використаємо той факт, що якщо нерухома точка відображення , то виконується рівність . Маємо : Оскільки областю визначення відображення є відрізок ,то нерухомою його точкою є точка

Приклад 8. Показати , що відображення

є стискуючим , і знайти його нерухому точку

Розв’язування. Нехай - довільні функції з простору Маємо :

Звідки отримаємо, що відображення є стискуючим із коефіцієнтом

Візьмемо початкове наближення нерухомої точки Тоді маємо :

Використавши формулу для суми членів геометричної прогресії, запишемо у вигляді

Знайдемо нерухому точку відображення

Отже, нерухомою точкою відображення є функція , тобто вона є єдиним розв’язком інтегрального рівняння