Поправки ранга два[править | править исходный текст]

Один из способов конструирования поправок ранга два заключается в построении сходящейся последовательности матриц  . В качестве начального значения   берут  ,   вычисляют по формуле:

После чего её симметризуют:

Однако полученная матрица больше не удовлетворяет квазиньютоновскому условию. Чтобы это исправить, процедуру повторяют. В результате на  -м шаге:

Предел этой последовательности равен:

При выборе различных   (не ортогональных  ) получаются различные формулы пересчёта матрицы  :

•  приводит к симметричной формуле ранга один;

•  приводит к симметричной формуле Пауэлла — Бройдена (PSB);

•  приводит к симметричной формуле Девидона — Флетчера — Пауэлла (DFP):

,

где 

Нетрудно проверить, что   ортогонален  . Таким образом добавление слагаемого   не нарушит ни квазиньютоновского условия, ни условия симметричности. Поэтому проводился ряд теоретических исследований, подвергавших последнее слагаемое масштабированию на предмет получения наилучшего приближения. В результате была принята точка зрения, что наилучшим вариантом является отвечающий полному отсутствию последнего слагаемого. Этот вариант пересчёта известен под именем формулы Бройдена — Флетчера — Гольдфарба — Шанно (BFGS):

Литература[править | править исходный текст]

• Гилл Ф., Мюррей У., Райт М. Практическая оптимизация = practical optimization.

[скрыть]

СВОЙСТВА СХОДИМОСТИ МЕТОДОВ

Определение.

Метод называется сходящимся, если неравенство

                

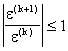
Выполняется на каждой итерации, где e^(k) = x^(k)-x^*.

 

Определение.

Алгоритм обладает сходимостью порядка r, если отношение

                

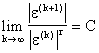
выполняется (конечно). Если r=1, то алгоритм обладает линейной скоростью сходимости. Если ещё при этом C=0, то алгоритм обладает суперлинейной скоростью сходимости. Если r=2, то скорость квадратичная.

Штрафные функции

Основная идея метода штрафной функции состоит в преобразовании задачи мин-и минимизации функции С соответствующими ограничениями, наложенными на в задачу поиска min без ограничений функции:

..

- штрафная функция. Необходимо чтобы при нарушении ограничений она «штрафовала» функцию Z, т. е. увеличивала ее значение. В этом случае min Z будет находится внутри области ограничений.

Задача минимизации формулируется следующим образом:

Сминимизировать функцию . (1)

при ограничениях 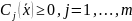(2)

Замечание: Ограничение « » всегда может быть записано .

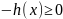Функцию записывают следующим образом:

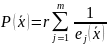
где 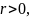тогда

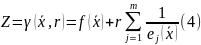
Если принимает допустимые значения, т. е. значения, для которых

, то Z принимает значения, которые больше соответствующих значений (истиной целевой функции)и разность можно уменьшать за счет того, что r может быть очень малым.

Но если принимает значения, хотя и являются допустимыми, но близки к границе ограничений, и по крайне мере одна из функций 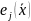близка к нулю, тогда значения функции и, следовательно Z станет очень великим. Т. о. влияние состоит в создании «гребня с крутыми краями» вдоль каждой границы области ограничений.

Пример. Используя штрафную функцию, заданную уравнением (4), минимизировать функцию 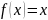при ограничениях 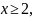т. е.

Минимальным значением функции является 2 при х=2.

Получим решение, используя метод штрафной функции.

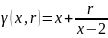
Построим график и покажем положение ее минимума для различных значений r (1; 0.25 и 0.01).

Область ограничений лежит справа от вертикальной прямой х=2. Нетрудно видеть, что последовательность точек Х1*, Х2*,Х3* стремится к точке Х* - истинному минимуму функции при наличии ограничений. Найдем минимум функции , прировняв ее производную к нулю:

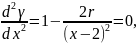
откуда 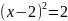или .

Для определения точки минимума найдем:

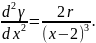
Подставив в последнее х, найдем, что минимум достигается при внутри области ограничений. Следовательно, функция имеет минимум, равный 2+2 при .

Тогда Х1* имеет координаты (3;4), Х2* - (2.5;3), Х3* - (2.1;2.2). Ясно, что при 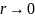минимум без ограничений функции приближается к значению 2 и минимальной точкой является 2.

В рассмотренном простом примере влияние штрафной функции мы получили зависимость минимума оптимизируемой функции от параметра r:

min .

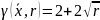В общем случае невозможно аналитически определить положение минимума функции 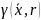. Для его определения необходимо обратится к численным методам (например, к методу Х-Д).

Обобщим результат, полученный в рассмотренном примере на случай общей задачи минимизации с ограничениями:

минимизировать функцию

при ограничениях .

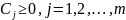Предположим, что 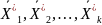–минимальные точки функции для убывающей последовательности 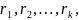стремящейся к нулю. Тогда последовательность точек сходится к оптимальному решению задачи с ограничениями при

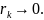
Следовательно и ,

где 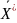- минимальная точка функции 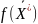при наличии ограничений.

Из изложенного следует, что алгоритм поиска минимума функции с ограничениями сводится к итерационной процедуре поиска минимумов в функции для убывающей последовательности

Причем каждая следующая точка является исходной точкой для нахождения следующего минимума .

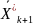Поскольку , то и

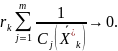
Следовательно процесс нахождения минимумов должен быть остановлен, когда станет достаточно малой величиной, т. е. «очень малой добавкой» и значению целевой функции .
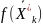