Править далее Квазиньютоновские методы

Этот класс методов основан на аппроксимации Гессиана некоторой положительно определенной симметрической матрицей H. Можно сказать, что если в методе Ньютона и его модификациях кривизна оптимизируемой функции учитывается Гессианом, то в квазиньютоновских информацию о кривизне накапливает матрица Н. Квазиньютоновские методы относятся к методам первого порядка, поскольку для пересчета Н на каждой итерации используется значение градиента в точках 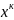и 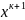, что принципиально отличает квазиньютоновские методы от методов второго порядка.

Матрицу Н называют метрикой. Поскольку метрика изменяется на каждой итерации, квазиньютоновские методы часто называют методами с переменной метрикой.

Расчетной формулой квазиньютоновского метода будет следующая формула:

Рассмотрим нахождение .

Разложим в ряд Тейлора градиент g(x) в окрестностях следующего к-ого приближения . Отбросив производные выше первого порядка и подставив 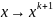будем иметь:

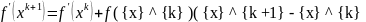
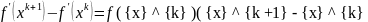
или

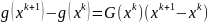
или

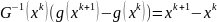
Заметим, что для квадратичных функций эта формула точная.

Для матрицы , которая будет аппроксимировать 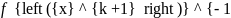должно выполняться условие:

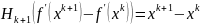
Такое условие называется квазиньютоновским. Методы оптимизации, для которых на каждой итерации выполняется квазиньютоновское условие, называются квазиньютоновскими.

Матрицу находят как:

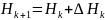
Перепишем квазиньютоновское условие в виде:

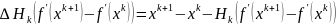
Такому условию удовлетворяет большое число матриц.

Прямой подстановкой можно показать, что для уравнение имеет следующее решение:

,

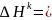
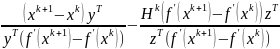где z и y – произвольные векторы размерности n.

Например, если 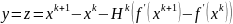, то получим метод Бройдена:

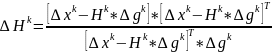, где

.

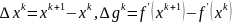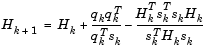,  BFGS

Метод дэвидона, флетчера, пауэлла

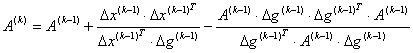; A⁽⁰⁾=I

Метод бройдена-флетчера-шенно

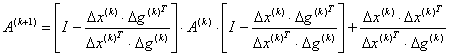
Метод обладает слабой по сравнению с ДФП чувствительностью к погрешности одномерного поиска.

+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

Разложим градиент   исходной функции в ряд Тейлора в окрестности точки очередного приближения   по степеням следующего шага алгоритма  :

Тогда оценка матрицы Гессе   должна удовлетворять равенству:

,

где 

это условие называют квазиньютоновским.

На каждой итерации с помощью   определяется следующее направление поиска  , и матрица   обновляется с учётом вновь полученной информации о кривизне:

,

где   — матрица, характеризующая поправку, вносимую на очередном шаге.

В качестве начального приближения   кладут единичную матрицу, таким образом первое направление   будет в точности совпадать с направлением наискорейшего спуска.

Поправка единичного ранга[править | править исходный текст]

Один шаг алгоритма даёт информацию о кривизне вдоль одного направления, поэтому ранг матрицы   полагают малым, и даже единичным:

где   и   некоторые вектора.

Тогда, квазиньютоновское условие примет вид:

Полагая, что предыдущая матрица   на очередном шаге квазиньютоновскому условию не удовлетворяет (т.е. разность в правой части не равна нулю), и что вектор   неортогонален  , получают выражение для   и  :

Из соображений симметричности матрицы Гессе, вектор   берут коллинеарным  :

Полученное уравнение называется симметричной формулой ранга один.