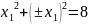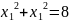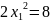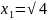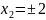- •Нелинейное программирование Постановка задачи безусловной оптимизации
- •Методы нулевого порядка. Метод Хука – Дживса.
- •Описание метода.
- •Методы первого порядка Градиентные методы
- •Градиентный метод с постоянным значением параметра шага.
- •Градиентный метод с дроблением шага.
- •Градиентный метод с оптимизацией шага.
- •Методы одномерной оптимизации.
- •Итерационные методы одномерной оптимизации
- •Править далее Квазиньютоновские методы
- •Метод дэвидона, флетчера, пауэлла
- •Метод бройдена-флетчера-шенно
- •Поправка единичного ранга[править | править исходный текст]
- •Поправки ранга два[править | править исходный текст]
- •Литература[править | править исходный текст]
- •Штрафные функции
Градиентный метод с оптимизацией шага.
Метод наискорейшего спуска.
Если
на каждой итерации выбирать
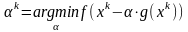 ,
то
получим метод наискорейшего спуска.
Таким образом, на каждой итерации
необходимо находить оптимальное значение
шага, минимизирующее целевую функцию.
Такую задачу называют задачей одномерной
оптимизации.
,
то
получим метод наискорейшего спуска.
Таким образом, на каждой итерации
необходимо находить оптимальное значение
шага, минимизирующее целевую функцию.
Такую задачу называют задачей одномерной
оптимизации.
Оптимальное
значение шага определяется из уравнения
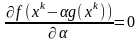 .
.
Определим
выражение для оптимального шага в случае
квадратичной целевой функции вида
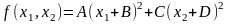 .
.
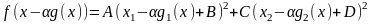 .
.
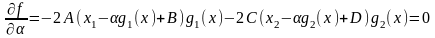 или
или
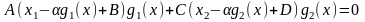 или
или
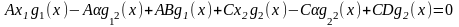 ,
откуда
,
откуда
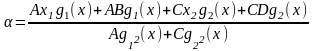 или
окончательно
или
окончательно
 .
.
В общем случае получить аналитическое выражение для шага в явном виде удается крайне редко, поэтому используются численные методы одномерной оптимизации.
Методы одномерной оптимизации.
Методы
одномерной оптимизации можно разделить
на итерационные и методы интерполяции.
В первых на каждой итерации выполняется
итерационный процесс сужения интервала,
на котором находится оптимальное
значение шага до заданной точности или
уточнения оптимального значения шага
по его начальному приближению. Во вторых
выполняется квадратичная или кубическая
интерполяции функции
 с
последующим аналитическим определением
значения оптимального шага.
с
последующим аналитическим определением
значения оптимального шага.
Итерационные методы одномерной оптимизации
К числу наиболее популярных численных методов одномерной оптимизации относятся: метод Больцано (деления интервала пополам), метод «золотого сечения» и пошаговый метод. Первые два метода ориентированы на поиск ext f (x) внутри фиксированного интервала (а,b) оси х, последний - на поиск ext f (x) в окрестности заданной точки х0.
М

1) определяется средняя точка интервала (а,b): с = (a+b)/2;
2) выбирается число (b-a)/2 (наиболее популярная рекомендация: =(b-a)/4) и определяются точки: x1=c- и x2=c+ ;
3) вычисляются значения функции в этих точках: f (x1) и f (x2);
4) если f (x1) f (x2), то интервал (а,b) стягивается в свою левую половину: b=c, в противном случае - в правую: а=с.
Для нового интервала (а,b) вновь выполняются действия п.п. 1) - 4). Процесс деления интервала продолжается до тех пор, пока его длина не станет меньше заданной точности: b-а . При завершении процесса поиска за точку минимума f (x) принимается середина последнего отрезка: x*=(а+b)/2.
Алгоритм метода Больцано (половинного деления, дихотомии).
Достаточные условия сходимости алгоритма метода Больцано:
а) функция f (x) непрерывна внутри интервала;
б) f (x) унимодальна на интервале (а,b), т.е. имеет внутри него единственный экстремум;
в) в некоторой окрестности искомой точки х* f (x) является монотонной
(с одной стороны возрастает, с другой - убывает).
Метод «золотого сечения»
Определение: «золотым сечением» отрезка называется его деление на две части таким образом, что отношение длины отрезка к его большей части равно отношению большей части к меньшей.
Следовательно, для отрезка единичной длины: 1/t = t/(1-t) t2+t-1=0
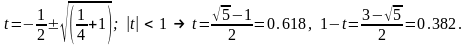
Алгоритм метода «золотого сечения» при поиске минимума функции f (x) включает операции:
интервал (а,b) делится точками х1, х2 в отношении «золотого сечения»: x1=a+(b-a)(3-
 )/2,
x2=b-(b-a)(3-
)/2;
)/2,
x2=b-(b-a)(3-
)/2;
2) вычисляются значения функции f (x1) и f (x2);
3) если f (x1) f (x2) , то от интервала (а,b) отсекается его правая часть:

4) в случае b=x2 точка x1 осуществляет «золотое сечение» нового интервала (а,b) и играет в нем роль точки х2, а точка х1 нового интервала определяется аналогично п.1); при а=х1 наоборот - х1=х2, а точка х2 нового интервала (а,b) определяется как в п.1).
Для нового интервала (а,b) вновь выполняются действия п.п. 2) - 4), причем в п.2) значение функции f (x) вычисляется один раз только для вновь определяемой точки х1 или х2. Процесс деления интервала продолжается до тех пор, пока его длина не станет меньше заданной точности: b-а .
При завершении процесса поиска за точку минимума принимается значение х* = (а+b)/2 .
Число модификаций исходного интервала (a,b) при использовании метода «золотого сечения» больше, чем при использовании метода Больцано (от интервала отсекается не половина, а 0.382 его длины), но количество вычислений значения функции f (x) существенно меньше. Поэтому в случаях, когда значение f (x) вычисляется достаточно долго, метод «золотого сечения» имеет заметное преимущество перед методом Больцано. Алгоритм метода «золотого сечения» сходится при тех же условиях что и метод Больцано.
Алгоритм метода золотого сечения.

Пошаговый метод применяется в тех случаях, когда интервал (а,b) оси х,
содержащий точку экстремума функции f (x) неизвестен, но известно, что экстремум находится в окрестности экспериментально найденной точки х0. Этот метод применяется на практике значительно чаще методов Больцано и «золотого сечения», т.к. условие сходимости его алгоритма намного проще: для этого достаточно, чтобы функция f (x) была непрерывна в окрестности х0.
При поиске минимума функции метод заключается в следующем:
выполняется пробный шаг от точки х0 с целью выбора направления
поиска: x = x0 + x (x ~ 0.5) и вычисляются значения f (х0), f (х);
если f (х) < f (х0), то величина основного шага, с которым осуществляется движение в направлении убывания функции, положительна (h > 0), в противном случае - отрицательна (h < 0);
3) движение в выбранном направлении с шагом h: xk+1= xk+h, k=0,1,2 ...
осуществляется до тех пор, пока f (xk+1) < f (xk);
4) если f (xk+1) ≥ f (xk), то при выполнении условия h < ε процесс поиска заканчивается, а если h ε, то шаг дробится: h=|h|/p, p > 1 и осуществляется возврат к п. 1) с начальной точкой х0 = xk.
В качестве коэффициента дробления шага p используют 2, 3, 5, но чаще всего p = e = 2.71828. По завершении процесса поиска за точку экстремума принимается значение x* =(xk+1 + xk)/2.
Алгоритм пошагового метода.
Метод сопряженных направлений
Метод сопряженных направлений часто называют методом сопряженных градиентов.
« Термин "метод сопряженных градиентов" – один из примеров того, как бессмысленные словосочетания, став привычными, воспринимаются сами собой разумеющимися и не вызывают никакого недоумения. Дело в том, что, за исключением частного и не представляющего практического интереса случая, градиенты не являются сопряженными, а сопряженные направления не имеют ничего общего с градиентами. Название метода отражает тот факт, что данный метод отыскания безусловного экстремума сочетает в себе понятия градиента целевой функции и сопряженных направлений.»
(Николой Некипелов).
Некоторые определения, используемые далее.
Скалярное
произведение двух
векторов записывается xTy
и представляет сумму скаляров:
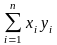 .
Заметим, что xTy
= yTx.
Если x и y ортогональны, то xTy
= 0. В общем, выражения, которые преобразуются
к матрице 1х1, такие как xTy
и xTAx,
рассматриваются как скалярные величины.
.
Заметим, что xTy
= yTx.
Если x и y ортогональны, то xTy
= 0. В общем, выражения, которые преобразуются
к матрице 1х1, такие как xTy
и xTAx,
рассматриваются как скалярные величины.
Первоначально метод сопряженных направлений был разработан для решения систем линейных алгебраических уравнений вида:
Ax = b (1)
где x – неизвестный вектор, b – известный вектор, а A – известная, квадратная, симметричная, положительно–определенная матрица. Решение этой системы эквивалентно нахождению минимума соответствующей квадратичной формы. Квадратичная форма – это просто скаляр, квадратичная функция некого вектора x следующего вида:
f(x) = (1/2)xTAx-bTx+c (2)
Наличие такой связи между матрицей линейного преобразования A и скалярной функцией f(x) дает возможность проиллюстрировать некоторые формулы линейной алгебры интуитивно понятными рисунками. Например, матрица А называется положительно - определенной, если для любого ненулевого вектора x справедливо следующее:
xTAx > 0 (3)
Н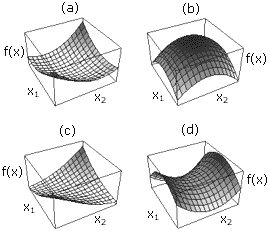 а
рисунке 1 изображено как выглядят
квадратичные формы соответственно для
положительно - определенной матрицы
(а), отрицательно - определенной матрицы
(b), положительно - неопределенной матрицы
(с), неопределенной матрицы (d).
а
рисунке 1 изображено как выглядят
квадратичные формы соответственно для
положительно - определенной матрицы
(а), отрицательно - определенной матрицы
(b), положительно - неопределенной матрицы
(с), неопределенной матрицы (d).
Рис. 1. Квадратичные формы для положительно-определенной матрицы, отрицательно-определенной матрицы, положительно-неопределенной матрицы, неопределенной матрицы.
То есть, если матрица А – положительно-определенная, то вместо того, чтобы решать систему уравнений 1, можно найти минимум ее квадратичной функции. Причем, метод сопряженных направлений сделает это за конечное число n или менее шагов, где n – размерность неизвестного вектора x. Так как любая гладкая функция в окрестностях точки своего минимума хорошо аппроксимируется квадратичной, этот же метод можно применить для минимизации и неквадратичных функций. При этом метод перестает быть конечным, а становится итеративным.
Рассмотрение метода сопряженных градиентов целесообразно начать с рассмотрения более простого метода поиска экстремума функции – метода наискорейшего спуска. На рисунке 2 изображена траектория движения в точку минимума методом наискорейшего спуска. Напомним суть этого метода:
в начальной точке x(0) вычисляется градиент, и движение осуществляется в направлении антиградиента до тех пор, пока уменьшается целевая функция;
в точке, где функция перестает уменьшаться, опять вычисляется градиент, и спуск продолжается в новом направлении;
процесс повторяется до достижения точки минимума.

Рис. 2. Траектория движения в точку минимума методом наискорейшего спуска.
В данном случае каждое новое направление движения ортогонально предыдущему. Метод сопряженных направлений предоставляет более разумный способ выбора нового направления движения. На рисунке 3 изображена траектория движения в точку минимума при использовании метода сопряженных направлений.
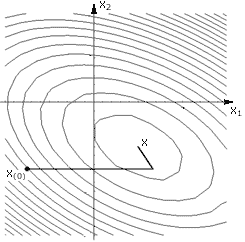
Рис. 3. Траектория движения в точку минимума при использовании метода сопряженных направлений
Определение сопряженности формулируется следующим образом: два вектора x и y называют А-сопряженными (или сопряженными по отношению к матрице А) или А–ортогональными, если скалярное произведение x и Ay равно нулю, то есть:
xTAy = 0 (4)
Сопряженность можно считать обобщением понятия ортогональности. Действительно, когда матрица А – единичная матрица, в соответствии с равенством 4, векторы x и y – ортогональны. Можно и иначе продемонстрировать взаимосвязь понятий ортогональности и сопряженности: мысленно растяните рисунок 3 таким образом, чтобы линии равного уровня из эллипсов превратились в окружности, при этом сопряженные направления станут просто ортогональными.
Выясним,
каким образом вычислять сопряженные
направления. Один из возможных способов
– использовать методы линейной алгебры,
в частности, процесс ортогонализации Грамма–Шмидта.
Но для этого необходимо знать матрицу
А, поэтому для большинства задач
(например, обучение многослойных нейронных
сетей) этот метод не годится. Поэтому
используется другой, итерационный
способ вычисления сопряженного
направления. Сопряженное направление
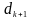 для следующей итерации вычисляется
следующим образом
для следующей итерации вычисляется
следующим образом
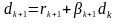 (5)
(5)
Формула
(5) означает, и в этом суть метода, что
новое сопряженное направление получается
сложением антиградиента
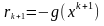 в точке поворота и вектора предыдущего
направления поиска
в точке поворота и вектора предыдущего
направления поиска
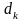 ,
умноженного на коэффициент
,
умноженного на коэффициент
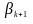 .
Начальным направлением
.
Начальным направлением
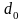 при старте из начальной точки
является
антиградиент
в этой точке
при старте из начальной точки
является
антиградиент
в этой точке
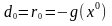 .
.
Существуют различные способы вычисления коэффициента . Наиболее известные и используемые из них – формулы Флетчера – Ривса и Полака – Райбера. Формула Флетчера – Ривса имеет вид
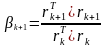 (6)
(6)
Формула Полака – Райбера :
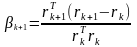 (7)
(7)
Метод Флетчера - Ривса сходится, если начальная точка достаточно близка к требуемому минимуму, тогда как метод Полака - Райбера может в редких случаях бесконечно зациклиться. Однако последний часто сходится быстрее первого метода.
Направления, вычисленные по формуле (5), оказываются сопряженными, если минимизируемая функция задана в форме (2), то есть, является квадратичной. Для квадратичных функций метод сопряженных градиентов находит минимум за конечное число шагов n (n – размерность пространства поиска). Для функций общего вида сопряженность нарушается, алгоритм перестает быть конечным и становится итеративным. При этом, Флетчер и Ривс предлагают возобновлять алгоритмическую процедуру (т.е. делать рестарт метода) через каждые n + 1 шагов.
Сходимость
метода Полака - Райбера обеспечивается
выбором
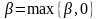 .
Это эквивалентно рестарту алгоритма
по условию
.
Это эквивалентно рестарту алгоритма
по условию
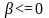 .
Рестарт алгоритмической процедуры
необходим, чтобы забыть последнее
направление поиска и стартовать алгоритм
заново в направлении наискорейшего
спуска.
.
Рестарт алгоритмической процедуры
необходим, чтобы забыть последнее
направление поиска и стартовать алгоритм
заново в направлении наискорейшего
спуска.
Алгоритм метода сопряженных направлений для минимизации функций общего вида (неквадратичных).
Вычисляется начальное направление поиска
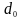 из произвольной начальной точки
,
определяемое антиградиентом
.
из произвольной начальной точки
,
определяемое антиградиентом
.Определяется оптимальное значение шага (одним из методов одномерной оптимизации) .
Переход в следующую точку , .
Вычисление антиградиента в этой точке .
Вычисление по формуле 6 или 7. Чтобы осуществить рестарт алгоритма, то есть забыть последнее направление поиска и стартовать алгоритм заново в направлении скорейшего спуска, для формулы Флетчера – Ривса присваивается
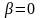 через каждые n + 1 шагов, для формулы
Полака -Райбера
.
через каждые n + 1 шагов, для формулы
Полака -Райбера
.
Вычисление нового сопряженного направления для следующей итерации .
Переход к пункту 2 или завершение алгоритма по критерию останова.
Из
приведенного алгоритма следует, что на
шаге 2 осуществляется одномерная
минимизация функции вдоль направления
.
Для этого можно воспользоваться любым
из рассмотренных методов одномерной
оптимизации. Например, методом Фибоначчи,
методом золотого сечения или методом
бисекций. Более быструю сходимость
обеспечивает метод Ньютона–Рафсона,
но для этого необходимо иметь возможность
вычисления матрицы
Гессе. В последнем случае, переменная,
по которой о![]() существляется
оптимизация, вычисляется на каждой
итерации по формуле:
существляется
оптимизация, вычисляется на каждой
итерации по формуле:
г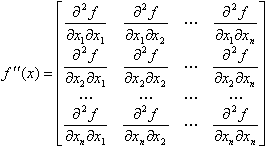 де
де
Матрица Гессе
Это дает основания некоторым авторам относить метод сопряженных градиентов к методам второго порядка, хотя суть метода вовсе не предполагает необходимым вычисление вторых производных.
Метод
сопряженных градиентов является методом
первого порядка, в то же время скорость
его сходимости квадратична. Этим он
выгодно отличается от обычных градиентных
методов. Например, метод наискорейшего
спуска и метод координатного спуска
для квадратичной функции сходятся лишь
в пределе, в то время как метод сопряженных
градиентов оптимизирует квадратичную
функцию за конечное число итераций. При
оптимизации функций общего вида, метод
сопряженных направлений сходится
несавнимо быстрее метода наискорейшего
спуска. При этом, в отличие от методов
второго порядка, не требуется трудоемких
вычислений вторых частных производных.
Рассмотрим ориентированный на MATLAB
практический алгоритм функции, реализующей
метод сопряженных направлений. Алгоритм
одномерного поиска представлен одним
общим блоком h=argminh
z(x+h*d)
и должен быть заменен конкретным
алгоритмом одномерной оптимизации.
Счетчик вычислений функции kz,
начальный шаг h
и значение целевой функции в начальной
точке f=z(x)
используются в алгоритме одномерной
оптимизации. Переменная dd=d*d'
имеет значение скалярного произведения
антиградиента
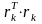 в
точке
,
переменная
ddn=dn*dn'получает
значение скалярного произведения
антиградиента
в
точке
,
переменная
ddn=dn*dn'получает
значение скалярного произведения
антиградиента
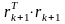 в точке
.
Процедура использует метод Флетчера
– Ривса и рестарт метода выполняется
через 4*n
итераций. Значение 4*n
получено в результате практической
оптимизации тестовой функции Розенброка,
обобщенной функции Розенброка семи
переменных и функции Пауэлла.
в точке
.
Процедура использует метод Флетчера
– Ривса и рестарт метода выполняется
через 4*n
итераций. Значение 4*n
получено в результате практической
оптимизации тестовой функции Розенброка,
обобщенной функции Розенброка семи
переменных и функции Пауэлла.
Ниже
представлены результаты оптимизации
квадратичной функции
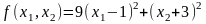 методом сопряженных направлений из
начальной точки x=[6
7] c
заданной погрешностью 1е-5. Здесь же
показана оптимизация
этой же функции для указанных условий,
выполненная методом наискорейшего
спуска. Обе оптимизирующие процедуры
sona3
и grosh3
для одномерной оптимизации используют
идентичные высокоэффективные алгоритмы
кубической интерполяции.
методом сопряженных направлений из
начальной точки x=[6
7] c
заданной погрешностью 1е-5. Здесь же
показана оптимизация
этой же функции для указанных условий,
выполненная методом наискорейшего
спуска. Обе оптимизирующие процедуры
sona3
и grosh3
для одномерной оптимизации используют
идентичные высокоэффективные алгоритмы
кубической интерполяции.
Алгоритм функции, реализующей метод сопряженных направлений.

Метод сопряженных направлений:
x = 6 7
e = 1.0000e-005
Elapsed time is 0.016378 seconds.
sona3: минимум найден,
итераций - 2 hmin=0.057981, hmax=0.47908
вычислений функции - 4
вычислений градиента - 4
x = 1.0000 -3.0000
f = 0
Метод наискорейшего спуска:
x = 6 7
e = 1.0000e-005
Elapsed time is 0.016322 seconds.
grosh3: оптимизация завершена, итераций - 23
вычислений функции 46
вычислений градиента - 46
hmin=0.057971, hmax=0.3634
x = 1.0000 -3.0000
f = 2.1387e-012
Результаты оптимизации функции методом сопряженных направлений и методом наискорейшего спуска.
Пример оптимизации тестовой функции Розенброка

x0 = 6 7
f =100*(x2-x1^2)^2+(1-x1)^2
Elapsed time is 0.020873 seconds.
sona3: минимум найден,
итераций - 32 hmin=5.2055e-006, hmax=2.2913
вычислений функции - 92
вычислений градиента - 92
x = 1.0000 1.0000
f = 5.4481e-015
x0 = 6 7
f = 100*(x2-x1^2)^2+(1-x1)^2
Elapsed time is 3.792633 seconds.
grosh3: оптимизация завершена, итераций - 25438
вычислений функции 50878
x = 1.0000 1.0000
z = 1.1308e-010

Литература
Н.Н.Моисеев, Ю.П.Иванилов, Е.М.Столярова "Методы оптимизации", М. Наука, 1978
А.Фиакко, Г.Мак-Кормик "Нелинейное программирование", М. Мир, 1972
У.И.Зангвилл "Нелинейное программирование", М. Советское радио, 1973
Jonathan Richard Shewchuk "Second order gradients methods", School of Computer Science Carnegie Mellon University Pittsburg, 1994.
Метод Ньютона
Является важнейшим методом второго порядка, поскольку на его основе построены практически все методы второго порядка.
Напомним, что методом второго порядка называется метод, использующий значения целевой функции, а также значения ее первых и вторых производных. Следовательно, необходимым условием использования метода является существование первой и второй производных целевой функции.
Метод Ньютона основан на квадратичной аппроксимации целевой функции в окрестности минимума. Поэтому для квадратичных функций он является точным и сходится за одну итерацию независимо от начального приближения.
Пусть - - тое приближение к точке минимума. Покажем, как методом Ньютона можно найти следующее приближение . Разложим целевую функцию в ряд Тейлора в окрестности , отбросив члены ряда выше второго
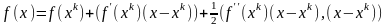
Определим
следующее приближение
как точку минимума
,
в которой
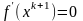
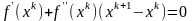 ,
откуда
,
откуда
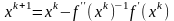 или
или
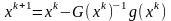 ,
,
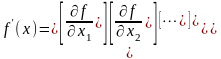 -
градиент в точке
;
-
градиент в точке
;
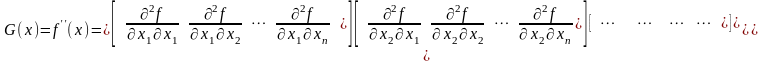 -
матрица Гессе (Гессиан) в точке
.
-
матрица Гессе (Гессиан) в точке
.
Пример.
Найти точку минимума квадратичной
функции
из начальной точки
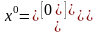 с точностью
с точностью
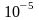 ,
критерий
завершения
,
критерий
завершения
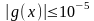 .
.
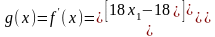 ;
;
 ;
;
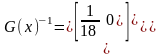 ;
;
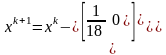 ;
;
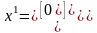 =
=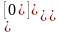 .
.
Проверим
критерий завершения:
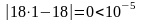 ;
;
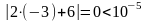 .
.
Таким образом, найдено точное решение за одну итерацию.
Оптимизация при наличии ограничений
(Условная оптимизация)
Обучение aml: lingualeo.comlrle – health(нет универсального метода)
Ограничения в виде равенств
Рассмотрим
задачу минимизации функции
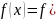 )
, где на переменную
)
, где на переменную
 наложены ограничения
наложены ограничения
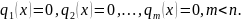 Для решения
таких задач разработан метод множителей
Лагранжа.
Для решения
таких задач разработан метод множителей
Лагранжа.
Метод множителей Лагранжа
1. Составить функцию Лагранжа
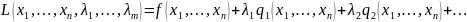
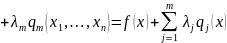 ,
,
где
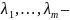 первоначально неизвестные множители
Лагранжа.
первоначально неизвестные множители
Лагранжа.
Эта
функция исследуется на безусловный
экстремум. (Т.о. задача минимизации с
ограничениями сводиться к минимизации
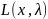 без ограничений, так как для допустимых
значений
, удовлетворяющих ограничениям,
без ограничений, так как для допустимых
значений
, удовлетворяющих ограничениям,
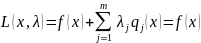 .
.
Необходимые
условия минимума
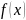 можно записать следующим образом
можно записать следующим образом
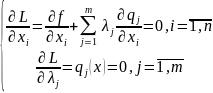
(Заметим,
что
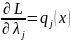 )
)
Приведенные
необходимые условия минимума являются
системой уравнений. Для каждого решения
этой системы в точке
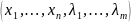 нужно исследовать знак дифференциала
второго порядка функции Лагранжа в этой
точке
нужно исследовать знак дифференциала
второго порядка функции Лагранжа в этой
точке
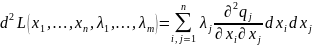 ,
,
здесь
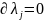 ,так как
,так как
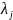 – это число.
– это число.
Если
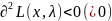 ,то точка (
,то точка (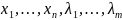 )
– точка условного максимума (минимума)
Найденный знак дифференциала
дополняет рассмотренные необходимые
условия до достаточных.
)
– точка условного максимума (минимума)
Найденный знак дифференциала
дополняет рассмотренные необходимые
условия до достаточных.
Пример
Найти условный экстремум функции
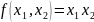 при
при
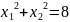 , т.е.
, т.е.
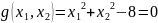
Составляем функцию Лагранжа
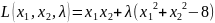
Находим
для
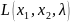 частные производные первого порядка
частные производные первого порядка
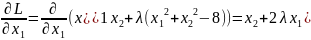
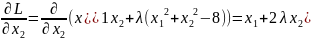
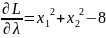
Система уравнений:

Из
1-го уравнения: если
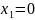 ,
то
,
то
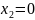 .
.
Подставим в 3-е уравнение:
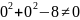 ,
т.е. 3-е уравнение не выполняется
,
т.е. 3-е уравнение не выполняется
Из
1-го уравнения
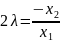 ;
;
Подставим это во 2-е уравнение:
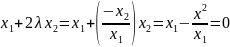
Отсюда
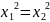
Подставим это в 3-е уравнение
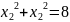 ,
откуда
,
откуда
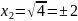 , но поскольку
,то
, но поскольку
,то
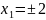
Получаем
четыре точки
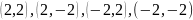
Если система уравнений имеет несколько решений, поступают следующим образом:
Найдем
значения исходной функции
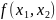 в полученных точках и среди этих значений
выберем наибольшее и наименьшее:
в полученных точках и среди этих значений
выберем наибольшее и наименьшее:
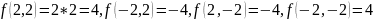
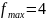 в
точках
в
точках
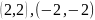
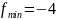 в
точках
в
точках
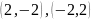
Можно решать так:
Из
1-го уравнения:
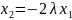
Подставим
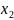 во 2-е уравнение:
во 2-е уравнение:
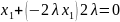
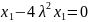
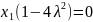
Если
,
то и
, но
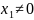 и
и
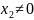 , иначе не выполняется 3-е уравнение
тогда
, иначе не выполняется 3-е уравнение
тогда
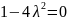
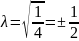
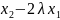
Откуда
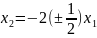 или
или
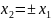
Подставим в 3-ое уравнение: