Нелинейное программирование Постановка задачи безусловной оптимизации
Целевая
функция задачи оптимизации представляет
собой нелинейную функцию
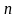действительных переменных
.
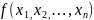Определить значения переменных, при
которых функция принимает минимальное
значение при отсутствии ограничений
на изменение переменных.
Задачи оптимизации, в которых нет ограничений на оптимизируемые переменные, называются задачами безусловной оптимизации.
Ввиду сложности задачи параметрической оптимизации применения классических метод поиска экстремума оказывается крайне сложным. Поэтому на практике предпочтение отдается поисковым (итерационным) методом оптимизации.
Все
поисковые методы выполняются по одному
алгоритму. Исходными данными в методах
поиска является начальная точка поиска
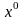и требуемая точность метода
.
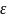Затем выбирается величина шага поиска
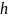и по правилу метода происходит получение
новых точек
по предыдущей точке
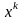при
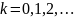таких, что
.
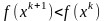Получение новых точек продолжается до
тех пор, пока не будет выполнено условие
прекращения поиска. Последняя точка
считается решением задачи оптимизации.
Все точки поиска составляют траекторию
поиска.
Методы поиска могут отличаться процедурой выбора шага (он может быть постоянным на всех итерациях или рассчитываться на каждой итерации), алгоритмом получения новой точки и условием прекращения поиска.
Методы
поисковой оптимизации принято
классифицировать по порядку производной
целевой функции, используемой для
получения новых точек. Методы, не
использующие производные целевой
функции, называются методами нулевого
порядка (прямыми), использующие первую
производную называются методами первого
порядка, вторую – методы второго порядка.
Чем выше порядок производной, тем более
обоснованным является выбор следующей
точки и тем меньше число итераций метода.
Эффективность поискового метода
определяется по числу итераций и по
количеству вычислений целевой функции
.
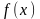Методы нулевого порядка. Метод Хука – Дживса.
Прямой метод Хука-Дживса был разработан в 1961 году, но и сейчас является весьма эффективным и оригинальным (1). Идея метода – поиск минимума состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которым в случае успеха следует поиск по образцу.
Описание метода.
А.
Выбрать начальную базисную точку
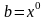и шаг длиной
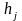для каждой переменной
.
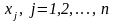В приведенном ниже алгоритме шаг
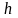одинаков
для всех переменных, однако указанная
выше модификация может оказаться
полезной, если значения переменных
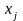отличаются
более чем на порядок.
Б.
Выполнить исследующий поиск вокруг
базисной точки
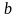с целью получения сведений о локальном
поведении функции
.
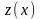Эти сведения будут использованы для
нахождения подходящего направления
поиска по образцу, с помощью которого
можно надеяться достичь большего
убывания функции. Исследующий поиск
выполняется следующим образом:
1.
Вычисляется значение функции
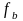в базисной точке
.
2.
К переменной
прибавляется длина шага
.
Таким образом, вычисляется значение
функции
,
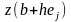где
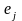– единичный вектор в направлении оси
.
Если это приводит к уменьшению функции,
то
заменяется на
.
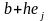В противном случае вычисляется значение
функции
,
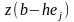и если ее значение уменьшилось, то
заменяется на
.
Если ни прибавление, ни вычитание шага
не приводит к уменьшению значения
функции, то точка
остается неизменной.
Когда будут
просмотрены все n
переменные, будем иметь новую базисную
точку, хранящуюся в векторе
.
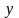В.
Если в результате исследующего поиска
уменьшение целевой функции было
достигнуто, т.е.
,
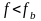то производится поиск по образцу. В
противном случае выполняется пункт Д.
Г. При поиске по образцу используется информация об убывании целевой функции, полученная в результате исследующего поиска, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура производится следующим образом:
1.
Разумно двигаться из базисной точки
в направлении
,
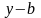поскольку поиск в этом
направлении уже привел к уменьшению
функции. Поэтому вычислим точку образца
.
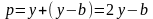2.
Запомним базисную точку
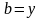и
значение целевой функции в ней
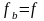на случай, если исследующий поиск после
шага по образцу окажется неудачным.
3.
Перейдем в точку образца, выполнив
,
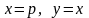и вычислим в точке образца значение
целевой функции
.
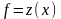4. Отметим выполнение шага по образцу установкой переменной flag=1 и выполним исследующий поиск вокруг точки образца по п. Б.2, как это делалось для базисной точки.
Д. Ситуация, когда исследующий поиск не привел к уменьшению функции.
1.
Выполняется проверка, где производился
исследующий поиск
в базисной точке (flag=0)
или в точке образца (flag=1).
2.
Если в точке образца, то восстановить
базисную точку, сохраненную в п. Г.2
,
,
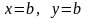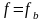установить flag=0
и выполнить исследующий поиск в этой
базисной точке.
3. Если в базисной точке, то повторить исследующий поиск, уменьшив длину шага. В практических реализациях метода удовлетворительным является уменьшение шага в десять раз от начальной длины (1).
Е. Завершить процесс, когда длина шага будет уменьшена до заданного малого значения.
Пример тестирующего скрипта
clear all
clc
x=[6 7]
global xf;
e=0.00001
h=1;
[f,x]=h_g('funak18',x,1), c='r';
plot(xf(1,:),xf(2,:),c)
hold on
x1=x(1)-5:0.1:x(1)+10;
x2=x(2)-5:0.1:x(2)+10;
[x1,x2]=meshgrid(x1,x2);
z=9*x1.^2+x2.^2-18*x1+6*x2+18;
contour3 (x1,x2,z,[1 5 17 39 57 101 151 199 251 301 373])
Пример файла с оптимизируемой функцией
function [y] = funak18(x )
%целевая функция
%
y=9*x(1)^2+x(2)^2-18*x(1)+6*x(2)+18;
Пример программной реализации метода Хука – Дживса
function [fb,x] = h_g(z,x,h)
%Минимизация функции f(x1,x2,...,xn) прямым методом Хука-Дживса
%без ограничений (по Б. Банди)
%
global xf;
z=fcnchk(z);
n=length(x);
y=x;
b=x;
kz=0;
flag=0;
kz=kz+1;
f=z(x);
fb=f;
kit=0;
xf(1,kit+1)=x(1);
xf(2,kit+1)=x(2);
nt=0;
tic
while h>=1e-8
% disp(['итерация ' num2str(kit) ', x=' num2str(x) ' f(x)=' num2str(f)])
nt=nt+1;
xf(1,nt)=x(1);
xf(2,nt)=x(2);
% disp(['исследующий поиск' ', x=' num2str(x)])
for j=1:n
x(j)=y(j)+h;
kz=kz+1;
if z(x)<f
y(j)=x(j);
else
x(j)=y(j)-h;
kz=kz+1;
if z(x)<f
y(j)=x(j);
else
x(j)=y(j);
end
end
f=z(x);
kz=kz+1;
end
kit=kit+1;
nt=nt+1;
xf(1,nt)=x(1);
xf(2,nt)=x(2);
if f<fb-1e-10
% disp('поиск по образцу')
p=2*y-b;
b=y;
x=p;
y=x;
fb=f;
f=z(x);
kz=kz+1;
flag=1;
else
if flag
y=b;
x=b;
f=fb;
flag=0;
% disp(['замена базисной точки' ', x=' num2str(x)])
else
% disp('уменьшение шага')
h=0.1*h;
end
end
end
toc
disp('h_g: минимизация завершена')
disp(['вычислений функции ' num2str(kz) ', итераций ' num2str(kit)])
end