Свободное падение зерен. Определение скорости свободного падения частиц различной формы. Параметры Лященко и их использование. Равнопадаемость тел при свободном падении.

Свободным падением называется падение одиночного тела в неограниченном пространстве или падение массы тел при небольшой объёмной концентрации твёрдого (не более 10%). Скорость свободного падения определяется по теоретическим уровням, по эмпирическим и интерполяционным формулам, по графикам и по таблицам, составленным на основе экспериментальных данных.

Скорость свободного падения определяется взаимодействием следующих сил: гравитационной, Архимедовой (подъёмной), силами гидродинамического сопротивления. При падении в неподвижной жидкости с начальной нулевой скоростью частица под действием сил тяжести будет постепенно увеличивать скорость падения; при этом также будет расти сила сопротивления. По истечении некоторого промежутка времени частица приобретает практически постоянную скорость падения, называемую конечной скоростью падения. С этого момента силы тяжести и архимедова уравновешиваются силами гидродинамиеского сопротивления. Для малых чисел Рейнольдса (Rе меньше 1) скорость падения шаров может быть рассчитана из того, что сила сопротивления выражается формулой:

Сила тяжести:

С учётом того, что сила Архимедова направлена вверх, а сила тяжести – вниз.

Формула Стокса: [см/с]

1<Re<1000

Формула Аллена: в степени 2/3 [см/c]

При практических расчётах она работает: Rе больше 30, но меньше 300.

Формула Антонычева – Нагорняка: (0,1<Re<5000):

- кинематический коэффициент вязкости.

– первый параметр Лященко. Ошибка в определении скорости по этой формуле не превышает 9%

При падении крупных частиц, когда число Рейнольдса больше 3000, формула Ньютона – Риттингера:

Все эти формулы имеют интерполяционный характер и получены на основании аппроксимации кривой Рейлея. И эти участки характеризуются определёнными формулами.

Параметры Лященко и их использование

Для определения вида частной формулы, которую следует применить в том или ином случае, необходимо знать число Рейнольдса, зависящее в свою очередь от скорости.

Лященко предложил использовать безразмерные параметры:

1. 

2. 

1-й и 2-й параметры Лященко используются для отнесения частиц к тому или иному диапазону по крупности, что позволит использовать ту или иную частную формулу для расчёта конечной скорости свободного падения (или размера частиц по известной конечной скорости падения).

Скорость свободного падения тел правильной несферической формы

Для тел правильной геометрической формы имеется определённая зависимость между характерным размером тела, его коэффициентом сферичности и скоростью падения (V_о).

За характерный размер тел принимают или диаметр равновеликого по объёму шара (d_э) или диаметр шара, поверхность которого равна поверхности тела (d_s). Форма тела характеризуются коэффициентом сферичности:

Для определения конечной скорости частиц правильной геометрической формы:

V_os=PV_o

P – коэффициент, зависящий от формы.

V_o – скорость падения шара эквивалентного телу по объёму.

Для приближенных расчётов (0,25<ω<1) следующие формулы:

, когда Re²ψ<350

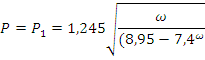
Re²ψ>500

Для промежуточных значений (20<Re_s<500; 350<Re²ψ<N).

Скорость падения тел следует определять графическим методом.

Скорость свободного падения частиц неправильной геометрической формы.

Для частиц неправильной формы чётких зависимостей между коэффициентом сопротивления, числом Рейнольдса и коэффициентом сферичности не установлено. Отличие по форме наблюдается не только между частицами разных минералов, но и между частицами одних и тех же минералов. Поэтому под скоростью свободного падения частиц определённой крупности (узкого класса крупности) следует понимать среднюю скорость; скорости отдельных частиц узкого класса крупности могут существенно отличаться от средней. Поэтому за размер частицы принимаем средний размер отверстий 2-х смежных сит (dср.), а в некоторых случаях эквивалентный диаметр шара (dэ). Для большинства минералов указанные величины, за исключением минералов, имеющих пластинчатую форму: d_э = (1,05 – 1,1) d_ср.

Самым простым способом приближённого определения скорости свободного падения частиц неправильной формы является табличный. Зная минерал и его крупность, по таблицам определяют приближённо скорость свободного падения.

Равнопадаемость частиц при свободном падении

Равнопадающие частицы – частицы разной крупности, плотности и формы, имеющие одинаковую конечную скорость свободного падения.

Равнопадаемость приводит к тому, что в один и тот же продукт разделения могут попадать при обогащении зерна разных минералов, а это ухудшает результаты разделения. Тоже самое может происходить и при классификации материала, когда в одноимённые продукты будут попадать и мелкие, и крупные частицы.

Отношение эквивалентных диаметров равнопадающих частиц называют коэффициентом равнопадаемости:

d_эл – более лёгкие

d_эт – более тяжёлые

С целью уменьшения количество равнопадающих зёрен перед гравитационным обогащением стремится предварительно расклассифицировать материал по шкале классификации с модулем, равным коэффициенту равнопадаемости.

Если в расчётах коэффициента равнопадаемости использовать уравнение скорости зёрен различной крупности при различных режимах движения, то можно получить частные формулы для определения коэффициента равнопадаемости:

Формула Стокса:

Rе больше 0, но меньше 1 – ламинарная область

Формула Риттлигера:

Rе больше 500 – турбулентный режим

Разделительные признаки при гравитационных процессах обогащения. Силы, действующие на частицу. Сопротивление среды и ее составляющие.

Различие в скорости движения частиц возникают за счёт разницы плотности, размера и формы. Эти свойства называются разделительными признаками, наиболее важные из них – плотность.

Для определения плотности минеральных зёрен используют различные методы:

1. Для относительно крупных кусков минерала плотность определяют путём их взвешивания на специальных весах – Марголена или Вестналя. При этом способе кусочек минерала сначала взвешивают на воздухе, а затем погружённым в воду, в которой его вес уменьшается согласно закону Архимеда: на вес объёма воды вытесненного тела. Разница в измеряемых весах даёт возможность вычислить плотность минералов. Данные весы устроены так, что стрелка сразу показывает искомую плотность.

2. Минерал взвешивается на воздухе, затем помещается в мерный стакан; фиксируют, на сколько поднялся уровень в нём, то есть находят массу зерна. Зная массу тела и объём, вычисляют плотность. Такой же способ используют для определения мелких зёрен – пиктометрический способ. Он заключается в следующем: взвешивают сначала мерный сосуд (пиктометр), далее с водой, налитой до метки; затем погружают туда частицы и взвешивают. Далее по формуле определяют плотность минералов и сростков:

А1, А2, А3, А4 – соответственно масса пустого пиктометра, масса пиктометра с минеральными зёрнами, масса пиктометра с минералами, наполненного водой до метки; масса пиктометра, наполненного водой.

Для повышения точности измерения используют дистиллированную воду; кипятят воду вместе с зёрнами, чтобы удалить остатки воздуха и пузырьки воздуха, прилипшие к поверхности частиц.

Значение плотностей чистых минералов можно найти в справочниках.

Другим разделительным признаком является крупность частиц. Крупность может измеряется различными способами:

1. Для частиц большого размера крупность может определятся измерением по 3 взаимно перпендикулярным направлениям с последующим вычислением среднего диаметра. Для частиц сферической формы за их крупность применяется диаметр шара.

2. Для мелких частиц их размер чаще всего определяется размером отверстий сит, через одно из которых частица проходит, а на другом остаётся.

При гравитационных процессах размеры частиц определяются косвенным способом путём измерения скорости падения зерна с последующим вычислением диаметра шара, соответствующего этой скорости.

А: Поскольку минеральные зёрна не имеют сферической формы, их крупность оценивают эквивалентным диаметром по объёму:

V_з- объем зерна; Q_з- масса некоторого N числа зерен.

Для узкого класса крупности:

Б: В Отдельных случаях за крупность зёрен принимают эквивалентный диаметр по поверхности:

d_s- диаметр шара, поверхность которого равна поверхности зерна;

S_з- площадь поверхности зерна.

Третьим разделяющим признаком является форма зерен. О форме зерен можно судить по коэффициенту сферичности:

S_ш и S₃- поверхности разнообъемных шара и зерна.

Коэффициент сферичности у частиц измеряется следующим образом:

ω=1 – шар;

0,75 < ω < 0,9 – округлые зерна;

0,6 < ω < 0,75 – угловатые зерна;

0,5 < ω < 0,6 – продолговатые зерна;

ω < 0,5 – пластинчатые зерна.