Приложения определенных интегралов

1. Геометрические задачи

А. Вычисление площадей

а) Вычисление площадей в прямоугольной системе координат.

Напомним геометрический смысл определенного интеграла - при определенных условиях он задает площадь криволинейной трапеции. Это позволяет находить площадь любой фигуры.

Точками А и В граница плоской фигуры D разбита на две части. Если известны уравнения “верхней” (дуга АМВ) и “нижней”(дуга ANB) границ:

АМВ: y = ₂ (x);

ANB: y = ₁ (x),

то площадь фигуры D можно найти как разность площадей, условно говоря, “большой “ и “малой” криволинейных трапеций:

S_D = S_aAMBb - S_aANBb =

Очевидно, что формула останется справедливой для любого расположения области D (выше или ниже оси Ох). Например, если часть области D находится ниже оси Ох, то ее (область) можно перенести вверх на некоторое расстояние С таким образом, чтобы D оказалась целиком выше оси Ох. Величина площади от этого не изменится:

Пример. Найти площадь сегмента параболы, т.е. фигуры, ограниченной дугой параболы x = y² и отрезком прямой х = а.

Решение. (ед²).

б) Вычисление площадей в параметрической форме.

Если уравнение верхней границы криволинейной трапеции задано в параметрической форме: причем   t  ;  () = a;  () = b,

то, сделав замену переменной, получим:

{замена .

Пример. Найти площадь эллипса с полуосями а и b.

В прямоугольной системе координат уравнение эллипса имеет вид:

Используя симметрию фигуры, найдем площадь четверти эллипса:

Используя параметрические уравнения эллипса в первой четверти:

и учитывая, что при х = 0, t = ; при х = а, t = 0, получим:

Тогда площадь эллипса будет: S =  ab.

в) Вычисление площадей в полярной системе координат.

Напомним, что площадь кругового сектора равна:

S _{кр.с. =}

где  - центральный угол ( в радианах),

R - радиус.

Рассмотрим криволинейный сектор, ограниченный лучами

 = ;  = ; и кривой r = f () (  ).

Разобьем криволинейный сектор лучами, выходящими из полюса под углами ₁ = ; ₂, ...., _n = , на n частей.

Обозначим  _i =  _i -  _i-1 и найдем площадь i - того (малого) криволинейного сектора, приближенно считая его круговым:

где - промежуточное значение угла между  _i-1 и  _i .

Тогда площадь всего кругового сектора будет равна:

переходя к пределу при , получим:

Пример. Найти площадь фигуры, ограниченной линией

(a² + y²)² = a²(x² - y²), называемой лемнискатой Бернулли (a > 0).

Т.к. переменные x, y входят в уравнение только в четных степенях, то фигура симметрична как относительно обеих осей координат, так и относительно начала координат. Перейдем к полярным координатам:

Подставив в уравнение линии, получим:

или

Построим линию, учитывая симметрию фигуры и условие r  0.

Площадь всей фигуры равна учетверенной площади заштрихованной части:

Б. ВЫЧИСЛЕНИЕ ДЛИН дуг кривЫХ

Если уравнение линии задано в прямоугольной системе координат:

y = f (x), причем f (x) и f (x) непрерывны на отрезке [a; b], то длиной такой криволинейной дуги называется предел, к которому стремится длина вписанной в нее ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих сторон к нулю.

Если участок х_i достаточно мал, то:

Сложив все “элементарные дуги” и перейдя к пределу, получим:

y_i = f(x_i) - f(x_i-1) = {по формуле Лагранжа} = f(C_i) x_i,

где С_i - промежуточное значение между x_i-1 и x_i.

Тогда:

Если кривая задана в параметрической форме:

причем x(t), x(t), y(t), y(t) непрерывны на отрезке [; ], то аналогичные рассуждения приведут нас к следующему результату:

Если кривая задана в полярной системе координат:

r = r(),     , то получим:

В. Вычисление объемов

Пусть дано тело, площадь каждого сечения которого плоскостью, перпендикулярной оси Ох, известно. Назовем эти сечения поперечными. Положение поперечного сечения зависит от абсциссы точки пересечения его с осью Ох.

Площадь сечения является некоторой функцией x : S = S(x), где x  [a;b].

Для вычисления объема тела применим общий метод.

1. Разобьем отрезок [a; b] на n произвольных непересекающихся частей точками: х₀ = а, х₁, х₂, ..., x_n-1, x_n = b.

Через точки деления проведем плоскости, перпендикулярные оси Ох. Тело разобьется на n слоев.

2. Обозначим объем слоя тела, соответствующий отрезку [x_i-1; x_i], через V_i, -

тогда

3. Вычислим объем i-го слоя. Для этого внутри [x_i-1; x_i] выберем точку С_i.

Вычислим S(C_i). Будем считать, что объем i- го слоя приближенно равен объему цилиндра, площадь основания которого равна S(C_i) и высота которого равна длине отрезка [x_i-1; x_i], т.е. x_i: V_i  S(C_i)x_i.

4. Объем всего тела:

5. Переходя к пределу при 0, где 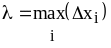получим:

Объем тела вращения.

Пусть тело получается вращением трапеции, ограниченной линией

y = f(x), x  [a;b], вокруг оси Ох, т.о. поперечным сечением служит круг, радиус которого равен соответствующей ординате кривой y = f(x).

(Если y < 0, то радиус будет равен ).

Площадь поперечного сечения S(x) = R² = [f(x)]², и мы приходим к формуле для объема тела вращения:

Замечание. Если требуется найти объем тела, образованного вращением трапеции, ограниченной линией x = f(y), y  [c;d], вокруг оси Oy, то получим:

Итак, с помощью определённого интеграла можно вычислить площади, длины дуг кривых и объёма тел.