Шпора №18

1- Коплексные числа …

Комплексными числами называются числа вида a+ib, где a и b - вещественные числа

Обозначения: Z,W Z=a+ib ReZ=a ImZ=b.

Умножение на i это поворот на 90 градусов. Z – это вектор его модуль

Z – называется чисто мнимым, если ReZ=0. Ось н называется линейной осью.

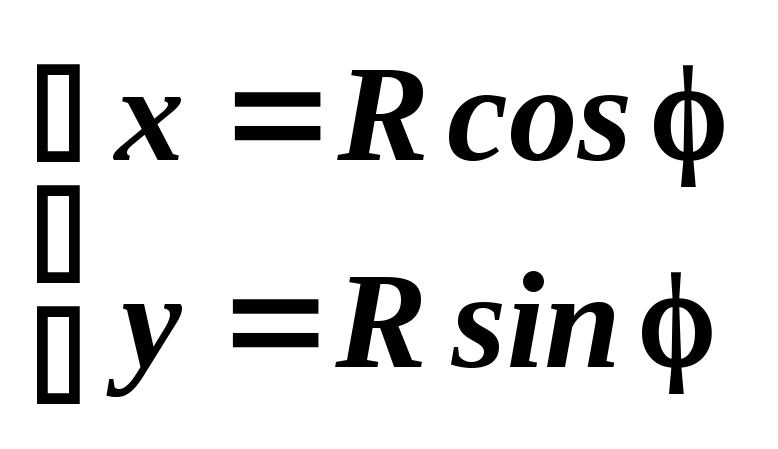
Формы записи: 1) Z=a+ib

2)

3) Z=Re^ij - показательная форма.

Где R – модуль Z, j-argZ , -p<j<=p, j- называется главным значением и обозначается argZ ,а все значения АrgZ= argZ+2pk (k=0,1,…).

Действия над комплексными числами.

Z=a+ib W=c+id

1) Z+_W=(a+_c)+i(b+_d)

2) ZW=(ac-bd)+i(bc+ad)

|ZW|=rr, arg(ZW)=argZ+argW=j+y. Смысл в том что число |Z| растягивается в |W| раз и поворачивается на угол y. (ZW)H=(ZH)W, (Z+W)H=ZH+WH, ZW= rre^i(j+y)

3) Степень : Zⁿ=ZZZ…Z (n-раз) argZⁿ=nargZ

Формула Муавра если |Z|=1 ,т.е. Z=(cosj+isinj), тогда Zⁿ =(cosj+isinj)ⁿ=(cosnj+isinnj)

Каждому комплексному числу Z соответствует сопряженное число

Они равны модулями, а углы противоположны по знаку.

4)

5) Извлечение корня. , wⁿ=z, z=r(cosj+isinj),w=r(cosy+isiny),rⁿ(cosny+isinny)=

= r(cosj+isinj) ,

если Z¹0, то имеет ровно n значений w₀,w₁,…,w_n-1 причем корни располагаются в вершинах правильного многоугольника, вписанного в окружность с радиусом r.

3-Функция КП…

Если каждому значению zÎG поставлено в соответствие одно(в случае однозначных функций) или несколько (в случае многозначных функций) значений wÎW, то говорят, что на множестве G значений Z задана функция w=f(az).

Односвязной областью называется такая область, для которой верно утверждение «Любая замкнутая область ограничивает область принадлежащую данной».

W=f(z), z=x+iy, w=u(x,y)+iv(x,y), где u-вещественная ,а v-мнимая части функции.

Функция w=f(z) устанавливающая соответствие между точками z и w , осуществляет отображение точек из области Z в область W.

Точки области G называется образами точек g при отображении w=f(z), а точки g называются прообразами соответствующих точек G.

Функция w=f(z) называется однозначной, если в каждой точке из области Z соответствует одна и только одна точка в плоскости W.

Если функция w=f(z) однозначна и такая, что обратная к ней функция z=F(w)(определенная на G) также однозначна, то тогда w=f(z) –однолистна на множестве g.

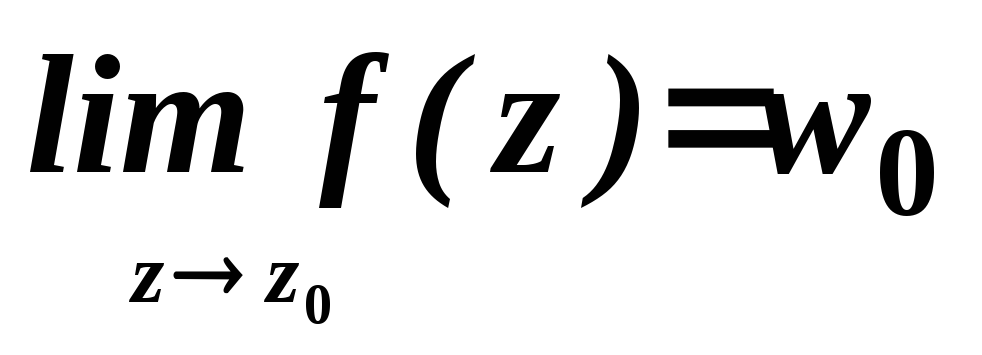Пусть w₀ ,z₀ конечные числа. Число w₀ называется пределом функции w=f(z)

" e>0 сущ. d(e)>0 т.ч.

|z-z₀|<d(*)=>|f(z)-w₀|<e(**)

Если w₀ или z₀ или оба вместе взять за бесконечность тогда неравенства меняются (*, **) или оба заменяются другими.Пример." e>0 сущ A т.ч.|z|>A=>|f(z)-w₀|

W=f(z)- непрерывна в точке z₀ если выполняются следующие условия:

1) f(z) определена в этой точке (.)z₀

2)$

3) f(z₀)=k

4-Понятие о ряде, Основ. Транс. Функции

Ряд называется сходящимся если  и причем конечный предел где Z_n-частичные суммы.

Если ряд из комплексных переменных сходится , сходится и ряды из мнимой и вещественной части этого числа .

Если сходится => то ряд называется абсолютно сходящимся.

Трансцендентные функции.

1) e^z+2kI=e^z –показательная функция.

2) Тригонометрические функции.

П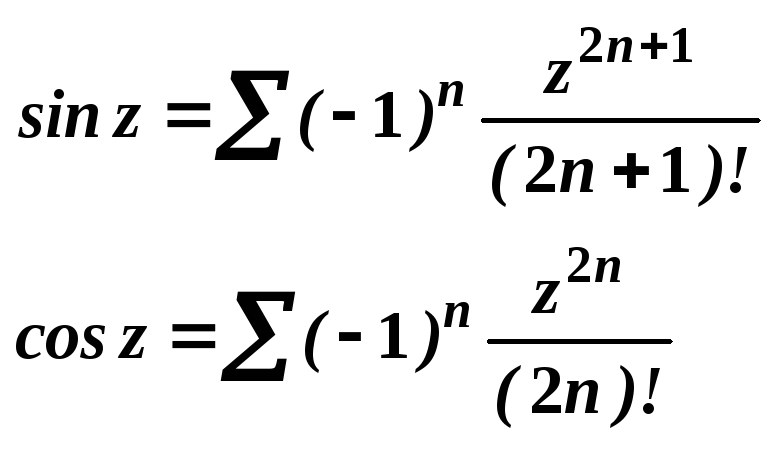ереодические с пери-одом 2 и имеют только действительные нули.

Формыла Эйлера

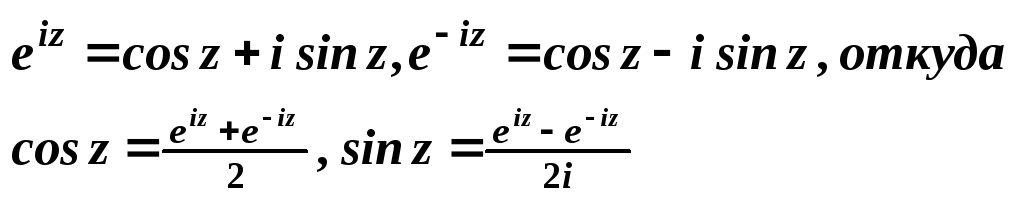
3)Логарифмическая функция обратная к показательной если e^w=z (z0)=>w=LnZ

Если w=u+iv |е^w|=e^ы, Arg e^w=v+2k, e^w=z=> |z|=e^u u=ln|z| то будем иметь LnZ=ln|Z|+iArgZ

Главное значение логарифма lnZ=ln|Z|+iargZ

Свойства логарифма остаются теже.

4)sinz=-ishiz, cosz=chiz, tgz=-ithiz, ctgz=icthiz

5)Обратные тригонометрические функции.

5- Производная ФКП.

Все формулы дифференцирования верны.

Рассмотрим w=f(z)- однозначна z=x+iy. Пусть z=x+iy –приращение z, тогда w=f(z+z)- f(z) приращение функции w.

Если предел отношения по любому закону, то этот предел называется производной функции f(z) в точке z.

Различие в требованиях существования производных функции w=f(z) и y=g(x)

по любому направлению все пределы равны.

_____________________________________________

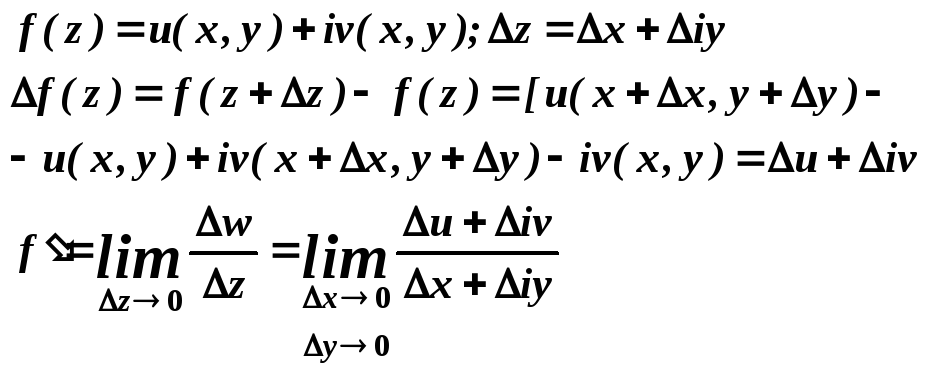6- Условие Коши-Римана.

Теорема: если  производная f^/(z), то выполняется условие =>

Доказательство: Пусть  f^/(z)<=>

По любому направлению z->0 и не зависит от этого стремления. z=x+iy=> в частности, z=x->0 и z=iy->0, т.е. по направлению ||Ox или || Oy

7-Аналитичность ФКП. Гармонические…

Если функция дифференцируема не только в точке z, но и в ее окружности, то она называется аналитической функцией в этой точке.

Функция аналитичная во всех точках некоторой области, называется аналитической в этой области.

Точки плоскости Z, в которой однозначная функция f(z) является аналитической, называются правильными точками f(z), а точки, в которых f(z) не является аналитической, называются особыми точками этой функции.(точки , в которых функция не определена относятся к особым).

Замечание. Свойства дифференцирования трансцендентных функций сохраняются.

Гармонические функции.

Гармоническими функциями называются функции, удовлетворяющие уравнению Лапласа:

Утверждение: Действительные и мнимые части аналитической функции f(z) в некоторой области являются в этой области гармоническими.

Доказательство: Пусть f(z)-аналитична =>

Действительно в области Д функции u,v удовлетворяют условию Коши-Рамена.

тогда продифференцируем, (+)по х (-) по у

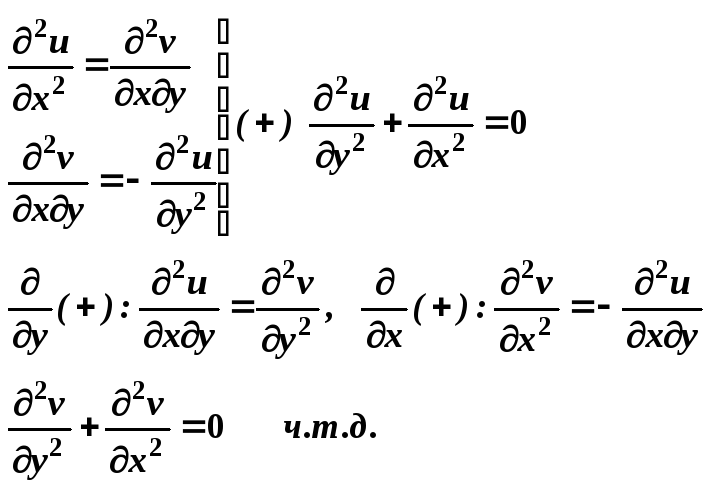
вывод: Re и Im части аналитчны, функции являются гармоничны , обратное неверно!

Пусть u,v - гармоничны функции=> u+iv=f(z)- не аналитична.

Две гармонические функции u(x,y) и v(x,y), удовлетворяющие условиям К-Р и являющиеся Re и Im частью функции – аналитичны.

Для сопряженных чисел x+iy и x-iy функции называются сопряженными.

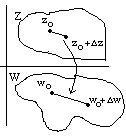
8-Геометрический смысл производной.

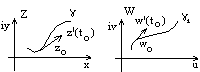
Пусть в плоскости Z задана точка z₀ и проходящая через нее кривая , равная =z=z(t), z(t)=x(t)+iy(t), пусть t=t₀, z₀=z(t₀)0 и  z^|(t₀)0, z^|(t₀)=x^|(t₀)+iy^|(t₀) 0

т.е. z^|(t₀)0=>x^|(t₀)0, y^|(t₀)0 => всегда  касательная => в точке z_o  z^|(t₀), причем x^|(t₀) и y^|(t₀) координаты касательной.

Функция f(z)-аналитична в окрестности точки z₀ и пусть f^/(z₀) 0, тогда запишем ₁ – образ  при отображении w=f(z)->ее уравнение имеет вид w=f(z(t)).

w(t)=f(z(t)) и w_o=w(t_o)=f(z(t_o))-образ z_o при w=f(z)

w^|(t_o)= f^| (z_o) z^|(t₀) (*) (w^|(t_o)0, т.к. f^| (z_o) и z^|(t₀) 0)=> касательная в точке w_o к кривой ₁ из (*)=> Arg w^|(t_o)=argf^|(z_o)+Argz^|(t₀). Отсюда видно, что f^|(z_o)=> argf^|(z_o) не зависит от кривой , поэтому f(z)-фиксирована , то Arg(w^|(z))=+Arg z^|(t₀), где =argf^|(z_o) не зависит от выбора кривой  через z_o.

=argf^|(z_o) равен углу, на который нужно повернуть касательную в точке z_o к любой кривой, проходящей через эту точку, чтобы получить направление касательной в соответствующей точке w_o к образу данной кривой  при

отображении w=f(z).(Если >0 поворот против часовой стрелки иначе против).

_____________________________________________

10-Геометрический смысл модуля произв.

|z| - расстояние от точки z_o до точки (z_o+z)

|w|- расстояние от точки w_o=f(z_o)до точки (w_o+w)

|w|/|z|- указывает в каком отношении в результате отображения меняются расстояния.

|f^/(z)| - коэффициент расстояния точки z₀ при отображении w=f(z).

Если k>1 => расстояние между точками увеличивается, иначе (если k<1) расстояние уменьшается.

9-Конформные отображения…

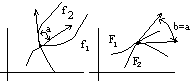
Отображение w=f(z), сохраняющие углы между касательными линиями называется конформным.

Отображение, сохраняющие углы между линиями и направлениями отсчета углов, называются конформными 1-го рода.

Отображение, сохраняющие углы по абсолютной величине, но изменяющие направление отсчета угла на противоположенное, называются конформными 2-го рода.

11&12-Интеграл ФКП, его свойства. Методы вычисления Интеграла ФКП.

Вычисление интеграла от функции f(z) комплексного переменного z сводится к вычислению обычных криволинейных интегралов, а именно:

где С кусочно-глаткая замкнутая или незамкнутая ориентированная кривая, лежащая в D.

Если f(z) аналитическая функция в односвязной области D, то интеграл не зависит от пути интегрирования. В этом случае

Если кривая С задана параметрическими уравнениями x=x(t), y=y(t) и начальные и конечные точки дуги С соответствуют значения параметра t₀ и t₁, то

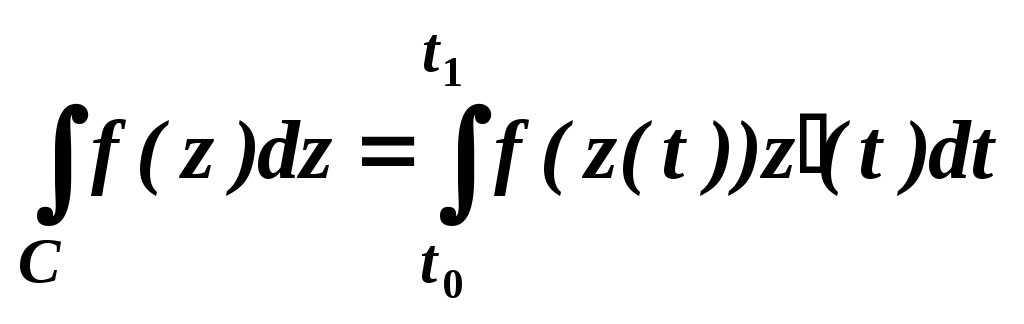
где z(t)=x(t)+iy(t).

Все свойства интегралов сохраняются для(такие как умножение на const…).

Если функция f(z) аналитична в односвязной D, содержащей точки z₀ и z₁, то имеет место формула Ньютона-Лейбница.

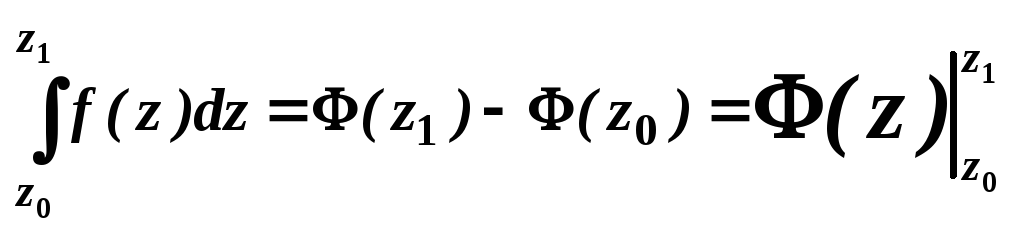
где (z)-какая-либо первообразная для функция f(z), т.ч. в области D  ^/(z)= f(z)

Также имеет место: интегрирования по частям, и замены переменной.

14-Интеграл от аналитической функции в односвязной области.

где n – целое, С- замкнуты контур.

1)n<0:

2)n0:

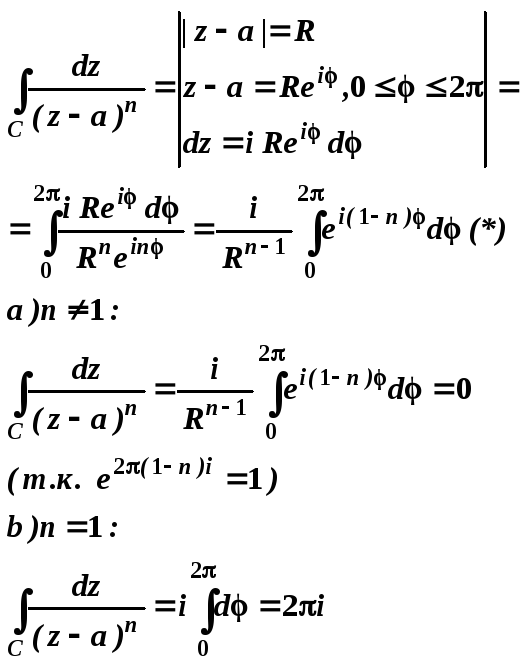
Если точка а внутри С то интеграл не равен 0.

Если контур С обходится против часовой стрелки k раз, то интеграл равен 2ki, иначе -2ki

13-Теорема Коши. (я его убил бы!)

не зависит от пути интегрирования при 

Теорема Коши: Если функция f(z) – аналитична в односвязной области G, ограниченная замкнутая контуром С, а также и на контуре С, то:

Доказательство: Пусть f(z) непрерывна.

Эти два интеграла тоже, что и криволинейный интеграл 2-го рода.

Так как f(z) аналитична выполняется условие Коши-Римана.

После подстановки условий К-Р можно сделать

вывод, что

(Теорема верна без предположения, что f(z) непрерывна) .

Пункт 2. Пусть область G многосвязная.

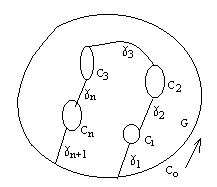
Рассмотрим многосвязную область G, ограниченную внешним контуром С₀ ивнутренними контурами С₁,С₂,…,С_n.

Пусть f(z)- аналитичная в области G и на контурах С₁,С₂,…,С_n. (С=С₀С₁… С_n).

Пусть

По замкнутому контуру С_k , обходится против часовой стрелки.

Соединим контура между собой дугами Область G разобьется на две односвязные области Г^/ и Г^// которые ограничиваю две односвязные области. Функция f(z) аналитична на контурах Г^/ и Г^// и в односвязных облостях которые они ограничивают. Из теоремы коши будем иметь:

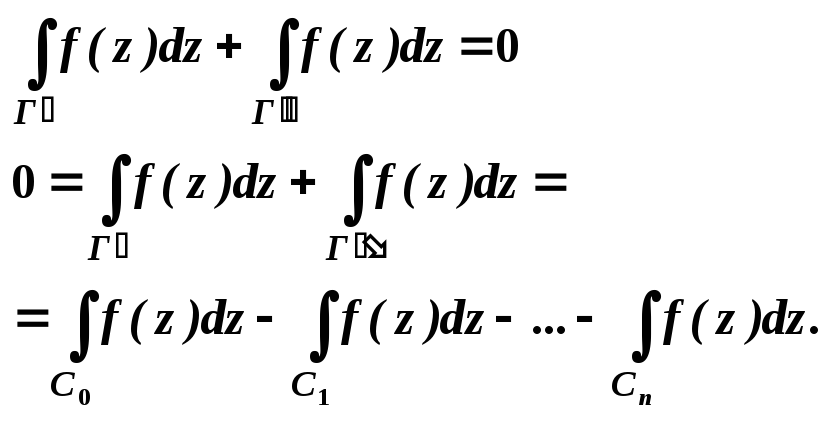
При сложении интегралов в левой части интегралы

сократятся в силу того, что при обходе по первому контуру мы берем их со знаком плюс при обходе по второму контуры берем со знаком минус.

П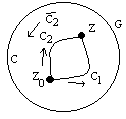ункт 3. Если интеграл f(z) по любому замкнутому контуру расположенному внутри области G равен 0 то интеграл по любой дуге принадлежащей G зависит только от начальной и конечной точек этой дуги и не зависит от пути интегрирования. Т.е. одинаков для всех дуг, имеющих общую начальную и конечную точки.

Доказательство:

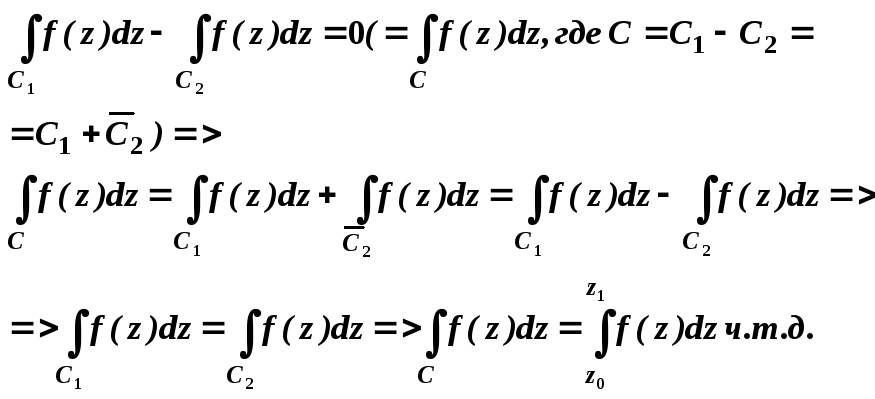
15-Интегральная формула Коши.

Пусть f(z)- аналитичная в односвязной области G и на контуре Г, ограничивающую эту область G и пусть точка Z любая точка внутри контура, тогда имеет место интегральная формула Коши:

Доказательство:  - окружность с центром в точке z и радиусом  причем G. По теореме Коши для составного контура будем иметь.

Доказав (**). Подставим в (***).

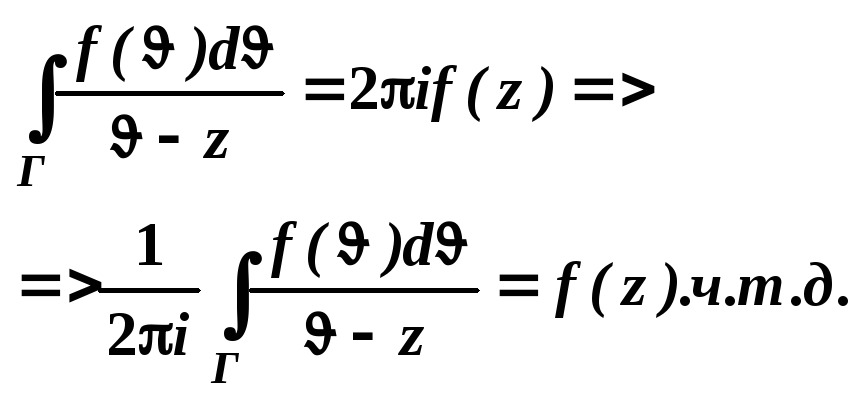
18-Функциональный ряд, сходимость, теорема Вейерштрасса.

Функциональный ряд- ряд члены которого являются функциями комплексной переменной.

Если существуетгде k конечное число => ряд сходится иначе расходится.

Остатком ряда называется R_n=S-S_n(z

)=f_n+1(z)+f_n+2(z)+…Если ряд сходится то

Теорема Вейерштрасса : Пусть на некотором множестве G ряд (см. вверх) сходится и можарируется некоторым сходящимся числовым рядом с положительными членами, т.е.  числовой ряд:а₁+а₂+а₃+…+а_n+…,т.ч.|f₁(z)|a₁, |f₂(z)|a₂,…, |f_n(z)|a_n , тогда ряд(см. вверх) сходится равномерно в G.

Верны все свойства числовых рядов .

Св-во: Если члены ряда аналитические функции в области G и ряд сходится равномерно, то его сумма также аналитическая функция в области G.

19-Степенной ряд. Теорема Абеля, круг сходимости.

Степенной ряд вида: C₀+C₁Z+C₂Z²+…+C_nZⁿ+…=

Теорема Абеля: Если степенной ряд сходится в точке Z₀ ,то он сходится и притом абсолютно во всех точках Z т.ч.|Z|<|Z₀| при этом в любом круге радиусом r, где |Z|£r<|Z₀| ряд сходится равномерно.

Доказательство. Выберем такое z, при котором выполняется условие |Z|<|Z₀| и рассмотрим степенно ряд. Обозначим |Z|=q|Z₀| , причем q<1. В силу необходимости сходимости ряда

его члены стремятся к 0 при n->¥. Следовательно, существует такая константа М, что |C_n||z₀|£M.

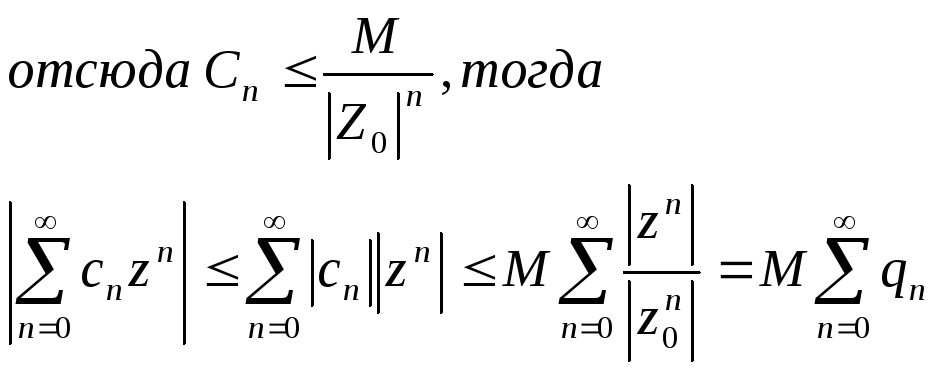Этот ряд сходится так как это геометрическая прогрессия , где q<1 по теореме сравнения 1. Доказана абсолютная сходимость ряда.

При |Z|£r<|Z₀| из доказанного выше, будем иметь

f(z).=> по теореме Вейерштрасе ряд сходится при |Z|£r<|Z₀| равномерно

Следствие. Если ряд расходится в точке z ,то он расходится вне круга с центром в точке 0 проходящей через точку z.

20-Ряд Тейлора.

Если в точке z₀ f(z) аналитична, то в окрестности этой точки она представима рядом

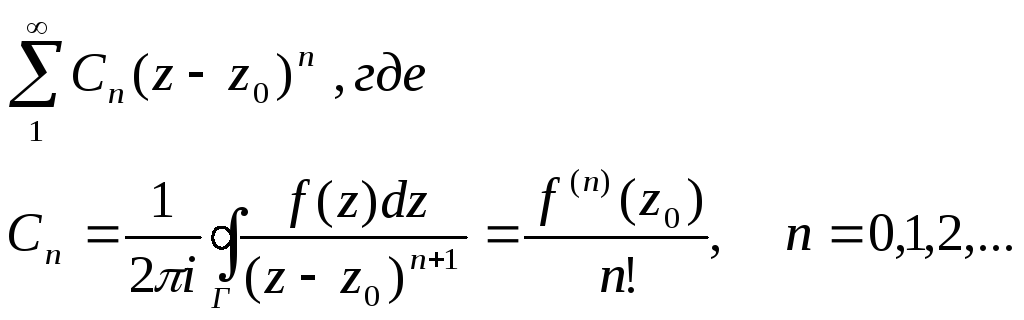
где Г- окружность с центром в точке z=z₀ , целиком лежащая в окрестности точки z₀ , в которой функция f(z) аналитична.

21-Нули аналитической функции.

Пусть функция f(z) является аналитеческой в точке z₀ . Точка z₀ называется нулем функции f(z) порядка (или кратности) n, если выполняется условия: f(z₀)=0, f^\(z₀)=0,…, f^(n-1)(z₀)=0, f⁽ⁿ⁾(z₀)0

Если n=1, то точка z₀ называется простым нулем.

Точка z₀ тогда и только тогда является нулем n-го порядка функции f(z), аналитической в точке z₀, когда в некоторой окрестности этой точки имеет место равенство: f(z)=(z- z₀)ⁿ(z), где (z) аналитична в точке z₀ и (z₀)0.

22-Ряд Лорана.

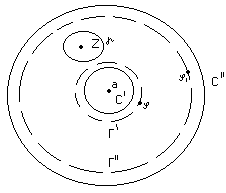
Пусть функция f(z) однозначная, аналитическая внутри кольца C^\C^\\ (C^\,C^\\ - концентрические окружности с центром в точки а). Проведем окружности Г^\ и Г^\\ т.ч. точка z Г^\Г^\\ и Г^\Г^\\ C^\C^\\.  - окружность с центром в точке z.  Г^\Г^\\. По теореме Коши для составного контура будем иметь:

По Интегральной формуле Коши :

тогда:

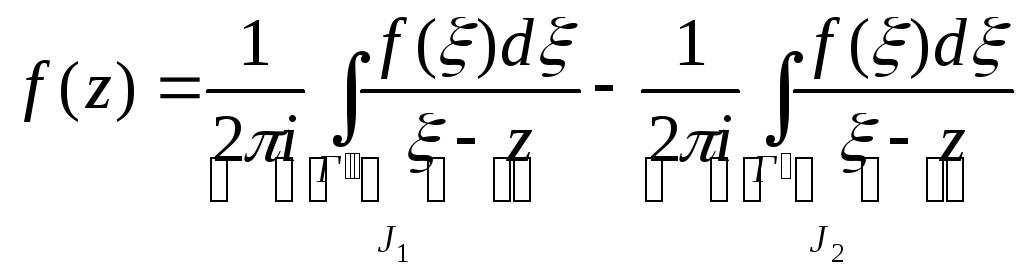
Рассмотрим два случая:

1)(J₁) пусть точка  лежит на Г^\\, тогда |‑a|>|z‑a|(т.е. (|z‑a|/|‑a|)<1)

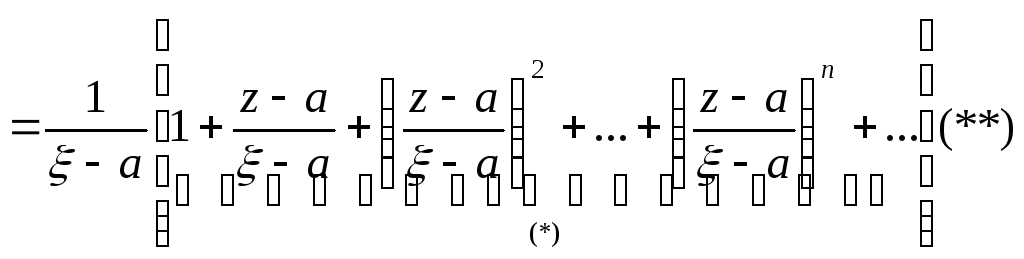
умножим (**) на f() и заметим что ряд (*) в правой части (**) сходится на окружности Г^\\ и при том равномерно т.к. геометрическая прогрессия со знаменателем q<1 сходится. Следовательно после умножения мы можем интегрировать.

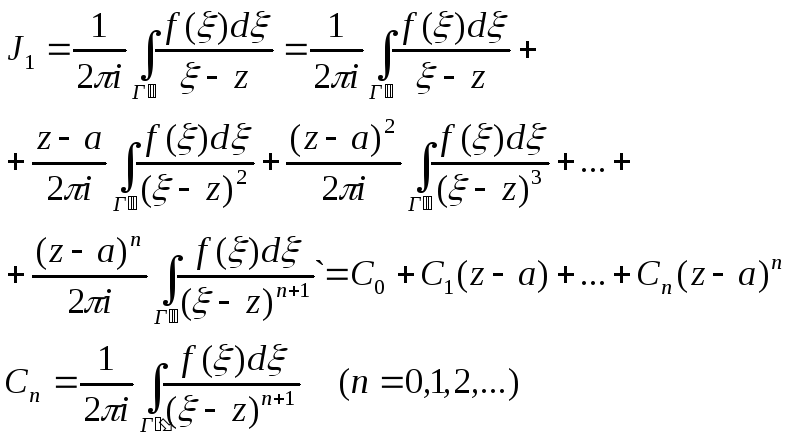2) рассмотрим для J₂:пусть точкаГ^\=>

|z-a|>|-a|((|-a|/|z-a|)<1) тогда

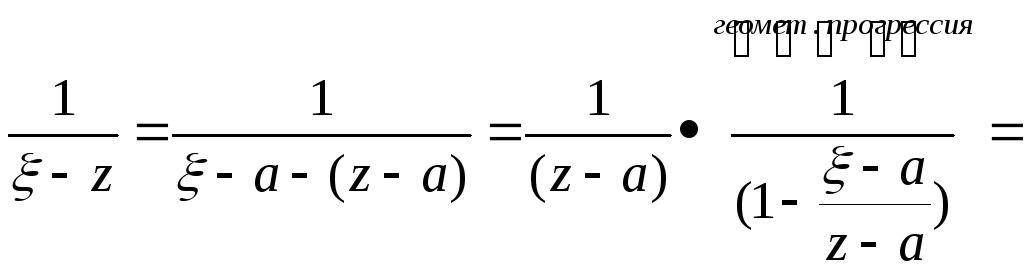
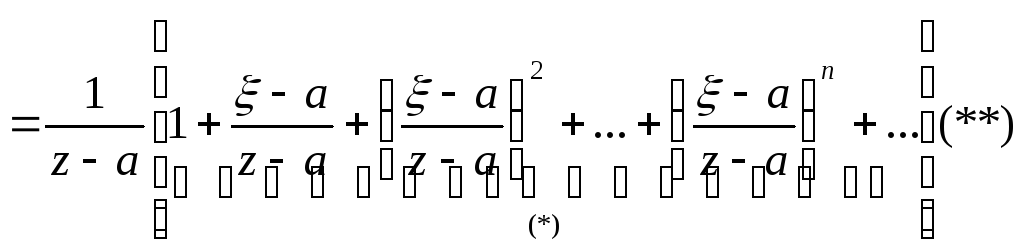
Ряд (**) сходится равномерно на Г^\.

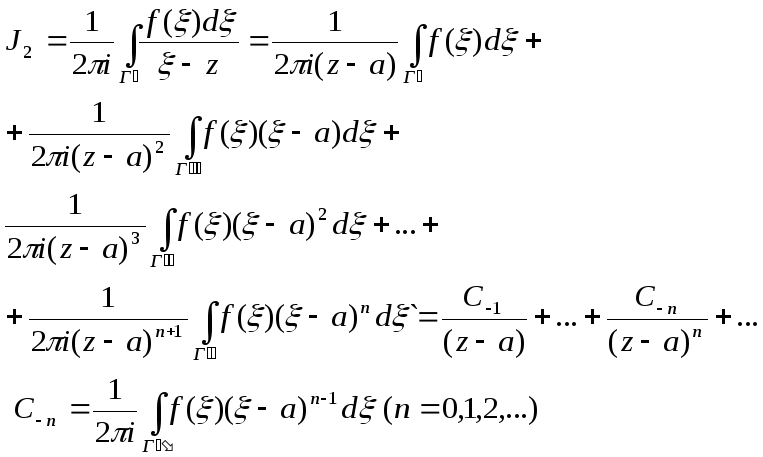При замене –n на n подынтегральное выражение остается верным для расчета коэфициентов.

В итоге мы получили формулу для разложения функции в ряд.Это разложение наз. раз. в р. Лорана

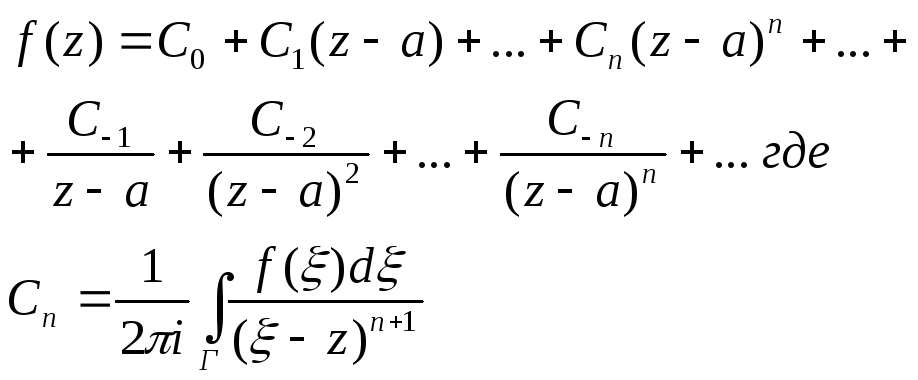
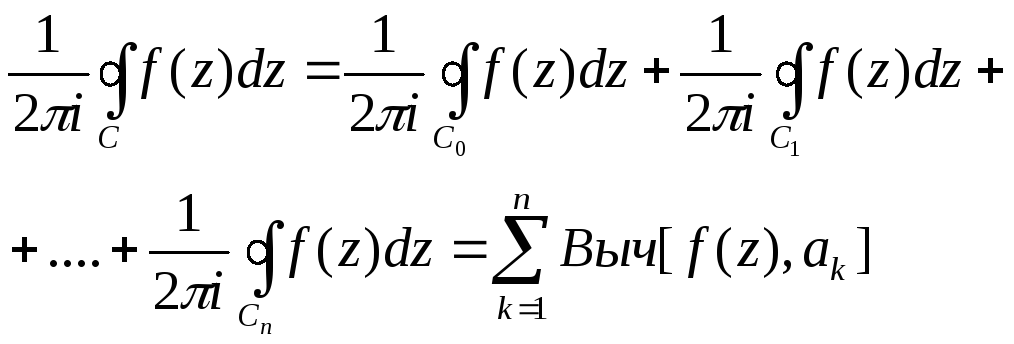Правильная часть ряда Лорана где n(0,1,2,3,4…),

главная же часть где n(-1,-2,-3,-4…).

23-И. О. точки, их классификация.

Точка называется и.о.т. ФКП f(z)если в некоторой окрестности точки а f(z) аналитична всюду кроме самой точки а, т.е. в окрестности точки а других точек нет.

Разложение функции f(z) в ряд Лорана сходящийся к f(z) во всех точках круга с центром в и.о.т. а, кроме самой точки а называется разложением функции f(z) в ряд Лорана в окрестности и.о.т. а.

Z₀- устранимая особая точка f(z),если предел f(z) равен конечному числу.

Пусть в окрестности точки а f(z) ограничена (т.е.  const=M>0, |f(z)|M в любой точке z из окрестности точки а) тогда в ряде Лорана главной части нет, есть только правильная. И этот ряд имеет сходимость во всех точках окрестности точки а, кроме самой точки а. Тогда пусть f(a)=C₀, будем считать точка а правильной точкой f(z).