Интеграл Фурье

Для всякой функции f(x) удовлетворяющим условиям Дерихле т.е.f(x) непрерывна или имеет конечное число разрывов 1го рода и абсолютно интегрируема т.е.

тогда f(x) представляется рядом Фурье на интервале (-l;l)

Пусть в некоторой точке x=x₀значение функции равно:

Подставим формулы коэффициента Фурье (1) в (2)

Подведём под интегралы cos(отx₀)cos(отx₀)=constи объединим:

косинус разности

nπ/l=ω_n– частота

Подставим значение частоты в (4)

Интервал (-l; l) расширим до ∞ и перейдем к пределу в (5)

вторая часть, правая, получаем:

выражение (7) написано для некоторой точки x, в которой функцияf(x) удовлетворяет условиям Дирихле заменивx₀=xаxзаменим наtвыражение (7) запишется в виде:

(8) - интеграл Фурье. Распишем cosразности аргументов в выражении (8).

Преподу дальше было лень рассказывать, так что продолжение смотрите или в библиотеке или просите у кого нибудь шпаргалку.

Задачи, приводящие к понятию двойного интеграла.

П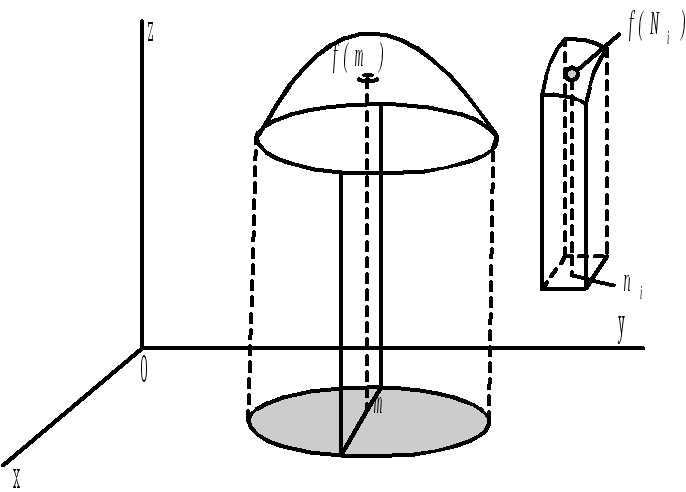усть имеем цилиндрическое тело, ограниченное сверху функциейF(x;y) снизу плоскостьюOxy, а сбоков цилиндром.

Вычислим объём данного тела – цилиндра.

Воспользуемся общей схемой применения интеграла:

1. Разобьем на n– частей.

2. Берём в области Ni,f(Ni)

3. Vi– объём =f(Ni)*δi

4. 

Чтобы вычислить точно объём цилиндроида, увеличим число разбиений до бесконечности и перейдём к пределу.

5.

Вычисления двойного интеграла в полярной и декартовой системе координат

Пусть проекция цилиндрического тела в полярной системе представлена виде:

d=dr*d*r

Пример:

В декартовой

Вдекартовой системе плоскость разбивается плоскостями || осям координат.

Сменим порядок интегрирования, тогда получим (там после равно всё написано, всё в одном уравнении).

При расстановке пределов в декартовой системе координат пользуемся правилом: внешний - от точки до точки; внутренний - от кривой до кривой.

Криволинейные интегралы. Якобиан.

Существует много систем координат. Связь между системами координат задаётся обычно некоторыми функциями перехода. Например декатрова система или шкала могут определяться формулами:

x=(U;V) иy=(U;V)

M₁(x₁; y₁) M₂(x₂; y₂) M₃(x₃; y₃) M₄(x₄; y₄)

x₁=(U+U;V) x₂=(U;V) x₃=(U;V+V) x₄=(U+U;V+V)

y₁=(U+U;V) y₂=(U;V) y₃=(U;V+v) y₄=(U+U;V+V)

Найдём связь между площадью элементарного участка dxdyиM₁;M₂;M₃;M₄.

Площадь M₁;M₂;M₃;M₄найдём, как площадь параллелограмма с известными координатами вершин

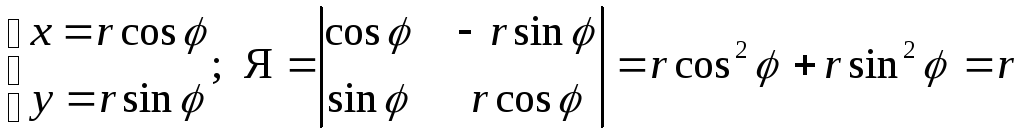
Я – якобиан.

Тройной интеграл и задачи приводящие к нему.

Пусть требуется вычислить массу тела неправильной формы с плотностью различной в каждой точке тела.m=V. Пусть плотность тела задана функцией=f(x,y,z). Скорректируем тело надxOyи воспользуемся общей схемой применения трехкратного интеграла:

1. Разобьем область и затем само тело на n-элементарных объёмов.

2. Предположим, что внутри элементарного объёма постоянна и равна значению функцииf(Mi), гдеMi– внутренняя точко элементарного объёма

3. mi=F(Mi)Vi

4. 

5. Чтобы получить точное значение массы тела перейдём к пределу, т. е. неограниченному разбиению тела на n-частей так, чтобыmaxдиаметр элементарной области стремился к 0. Диаметром элементарной области наз. расстояние между двумя наиболее удалёнными точками:

Вычисление 3 кратного интеграла в декартовой системе координат.

Если объём тела представляет собой параллелепипед, то:

При расстановке и смене порядка интегрирования пользуются правилом: «от точки до точки, от кривой до кривой, от поверхности до поверхности».

Вычисление тройного интеграла в цилиндрической и сферической системе координат.

Чтобы упростить процедуру вычисления кратного интеграла пользуемся различными приемами координат. Т.к. в декартовой системе вычислять удобно тройной интеграл если область интегрирования имеет прямоугольную форму. А если область имеет цилиндрическую или сферическую, то нужно перейти к полярной, цилиндрической или сферической СК. Чтобы вычислить тройной интеграл в цилиндр или сферич СК нужно:

1. Перейти в соответствующей СК к подынтегральной функции.

2. Вычислить Я и подставить его в интеграл

3. Расставить пределы интегрирования в соответствующей СК.

Для примера запишем тройной интеграл в сферической СК.

согласно рисунку:

Найдём Якобиан:

=r²sin

Следовательно, если при (x,y,z)(r,,) подынтегральная функция примет видf(x,y,z)g(r,,), то

Для примера вычислим объём шара. Для этого возьмём ⅛ часть его объёма

Что и требовалось доказать.