Ряд Тейлора

Как известно, ранее была получена формула Тейлора вида:

Функция f(x) является суммой степенного ряда или говорят, что функцияf(x) представлена степенным рядом (1)

f(x)=e^x

Положим в ряде Тейлора a=0 ряд Макларена.

f(x)=f(0)

f‘(x)=e^xприx=0f(0)=1

f`(x)=e<sup>x</sup>приx=0f`(0)=1

… …

f ⁽ⁿ⁾(x)=e^x при x=0 f⁽ⁿ⁾(0)=1

так как остаток ряда R_n(x) есть разность между суммойS(x) иS_n(x)

Rn(x)-S(x)-Sn(x), то приn∞ величина остатка0, что показывает, что данный функциональный ряд сходится, это подтверждает теорема по который функциональный ряд сходится и сумма его равнаf(x), если остаточный член рядаRn0, аf(x) имеет все производные.

xⁿ⁺¹ и (n+1)! стремятся в ∞ приn∞ их соотношение вообще неопределённость и подлежит исследованию.

Ряд Фурье. Коэффициенты ряда. (тригонометрические)

Тригонометрические функциональные ряды находят большое применение почти во всех технических приложениях, где анализируются колебательные процессы.

При рассмотрении тригонометрических рядов применяются некоторые интегралы от тригонометрических функций.

Рассмотрим условия ортогональности данных функций:

1) sinx, sin(2x), sin(3x), …, sin(nx), …

2) cosx, cos(2x), cos(3x), …, cos(nx), …

Если вектор А имеет координаты {а₁, а₂, а₃, …, а_n, …} , а В имеет координаты {b₁,b₂,b₃, …,b_n, …} А перпендикулярно В когда их скалярное произведение (оно равно сумме произведений соответствующих координат) равно 0.

Значит система ортогональна. Рассмотрим функцию:

Найдем неизвестные коэффициенты а₁, а₂, а₃, …, а_nиb₁,b₂,b₃, …,b_n. Для этого проинтегрируем равенство (1) на интервале (-;). Найдем а₀, затем умножим (1) наcosnx, найдемa_n, затем умножим (1) наsinnxи найдемb_n.

Условия и ряд Дирихле

Условия. Представление о функции f(x) тригонометрическим рядом

было не обоснованным, так как возникает два вопроса:

1. Ряд 1 сходится ли

2. Если да, то сумма его равна ли f(x).

Рассмотрим условия накладываемые на функцию f(x)

1. Функция f(x) – непрерывна, а если разрывна, то разрывы должны быть первого рода, причём число разрывов на интервале минус пи – пи – конечно.

2. Промежуток (-;) можно разбить на конечное число промежутков, в которыхf(x) непрерывна и монотонна. Эти два условия называются условиями Дирихле.

Теорема Дирихле: если функцияf(x) на интервале минус пи – пи удовлетворяет условиям Дирихле, то ряд Фурье этой функции сходится и сумма этого ряда равна:

1. Ф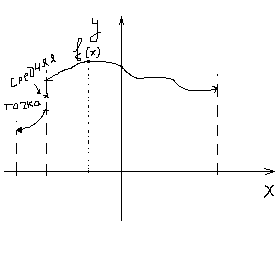ункцииf(x) в точках непрерывности.S(x)=f(x)

2. В точках разрыва первого рода сумма равна s(x)=[f(x+0)+f(x-0)]/2

3. На концах промежутка (-;)S() = [f(-+0) +f(-0)]/2

Рядом Дирихле называется знакоположительных ряд.

- Ряд Дирихле

При =1 ряд Дирихле становится гармоническим.

Для исследования его сходимости используем интегральный признак сходимости.

этот ряд сходятся или расходятся одновременно. Такоё интеграл сходится при > 1 и расходится при≤ 1.

Разложение функции на интервале (-l;l)

Если мы имеем интервал (-π;π) для некоторой переменной ψ то при переходе к интервалу (-l;l) для переменнойxнужно сделать масштабный переход.

Пусть некоторая функция φ(ξ) представлена рядом на интервале [-π; π]

заменим переменную ζ по (1), тогда