Методика Пірсона

Для того, щоб перевірити з допомогою методики Пірсона, чи результати вимірювань належать до нормального розподілу, додатково необхідно вирахувати дисперсії характеристик асиметрії та ексцесу D(b₂), які залежать лише від числа спостережень n і відповідно визначаються:

;

і перевірити виконання наступних умов:

і

Якщо ці умови виконуються, то студент робить висновок що результати вимірювань належать до нормального розподілу і навпаки.

4. Вирахування довірчих меж випадкової похибки результату вимірювання

Довірчі межі випадкової похибки результату вимірювання вираховують на підставі виправленого ряду результатів спостережень та коефіцієнту Ст’юдента (див. табл. 6 додатку).

Випадкова складова похибки результату вимірювання визначається за формулою:

,

де – оцінка середньоквадратичного відхилення результату вимірювань;

t – коефіцієнт Ст’юдента, знаходимо за таблицею 6 у додатку для заданих числа f=n-1 ступеня вільності та довірчої ймовірності P_д шляхом інтерполяції.

5. Приклад

Необхідно здійснити опрацювання результатів спостережень, а саме:

1. Виявити та усунути з ряду результатів спостережень промахи.

2. Вирахувати результат вимірювання та оцінки середнього квадратичного відхилення результату спостереження та вимірювання.

3. Перевірити належність результатів вимірювань до нормального розподілу за допомогою складового критерію та методики Пірсона.

4. Вирахувати довірчі межі випадкової похибки вимірювання ПВП.

При вимірюванні температури t були отримані наступні результати, С

№ п/п	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
t,С	20,42	20,43	20,40	20,41	20,43	20,42	20,41	20,39	20,30	20,40	20,44	20,43	20,42	20,41	20,39	20,41	20,40

1. Для виявлення в результатах вимірювання фізичних величин грубих похибок (промахів) їх необхідно розташувати в порядку зростання або спадання, тобто утворити варіаційний ряд:

17	1	*2	*3	*4	*3	*3	1
№ п/п	1	2-3	4-6	7-10	11-13	14-16	17
№ досл	9	8,15	3,10,17	4,7,14,16	1,6,13	2,5,12	11
t,C	20,30	20,39	20,40	20,.41	20,42	20,43	20,44
t,C	-0,106	-0,016	-0,006	0,004	0,014	0,024	0,034
t2	0,01124	0,000256	0,000108	0,000016	0,000196	0,000576	0,001156

Середнє арифметичне значення температури:

Незміщена оцінка середньоквадратичного відхилення результатів вимірювання:

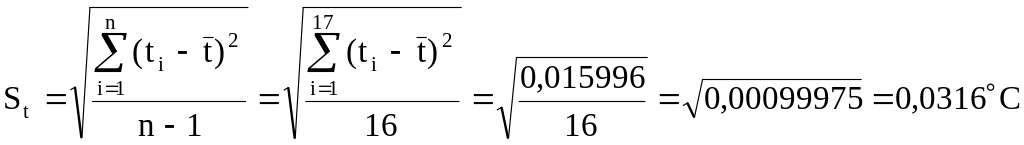
Для довірчої ймовірності Р=95% і числа спостережень n=17 (f=n-1=16) з таблиці 1 знаходимо r=2,577.

Для сумнівного 1-го (9-го) результату:

r₁=3,354 > r=2,577 – перевищує допустиме значення

Для сумнівного 17-го (11-го) результату:

r₁₇=1,076 < r=2,577 – не перевищує допустиме значення

Отже, 1-й результат t=20,30C є грубою похибкою і його виключаємо.

Після цього вираховуємо нові значення оцінок параметрів розподілу:

=16	*2	*3	*4	*3	*3	1
№п/п	1-2	3-5	6-9	10-12	13-15	16
№досл	8, 15	3, 10, 17	4, 7, 14, 16	1 ,6, 13	2, 5, 12	11
t,C	20,39	20,40	20,41	20,42	20,43	20,44
t	-2,3*10-2 -4,6*10-2	-1,3*10-2 -3,9*10-2	-0,3*10-2 -1,2*10-2	0,7*10-2 2,1*10-2	1,7*10-2 5,1*10-2	2,7*10-2 2,7*10-2
t2	5,29*10-4 10,58*10-4	1,69*10-4 5,07*10-4	0,09*10-4 0,36*10-4	0,49*10-4 1,47*10-4	2,89*10-4 8,67*10-4	7,29*10-4 7,29*10-4
t3	-12,67*10-6 -24,334*10-6	-2,197*10-6 -6,591*10-6	-0,027*10-6 -0,108*10-6	0,343*10-6 1,029*10-6	4,913*10-6 14,739*10-6	19,683*10-6 19,683*10-6
t4	27,9841*10-8 55,9682*10-8	2,8561*10-8 8,5683*10-8	0,0081*10-8 0,0324*10-8	0,2401*10-8 0,7203*10-8	8,3521*10-8 25,0563*10-8	53,1441*10-8 53.1441*10-8

Середнє арифметичне значення температури:

.

Незміщена оцінка середньоквадратичного відхилення результатів вимірювання:

.

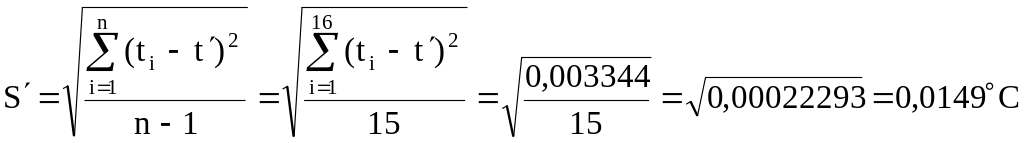Найбільше відрізняється від нового середнього 16-ий результат .

Для сумнівного 16-го (11-го) результату:

.

З таблиці 1 для n=16 (f=16-1=15) i P=95% знаходимо r=2,551 > r₁₆=1,80. Отже, 16-й результат і тим більше всі інші результати не є грубими похибками і вони залишаються в ряді результатів.

У зв’язку з тим, що S є меншим від попереднього значення S в 2 рази, то і розсіювання результатів практично в 2 рази стало меншим.

.

2. Вважаємо, що ряд значень вимірювання є виправленим і результатом вимірювання температури є його середнє арифметичне .

Медіана , мода .

Оцінка середнього квадратичного відхилення результатів вимірювань вираховується за формулою:

.

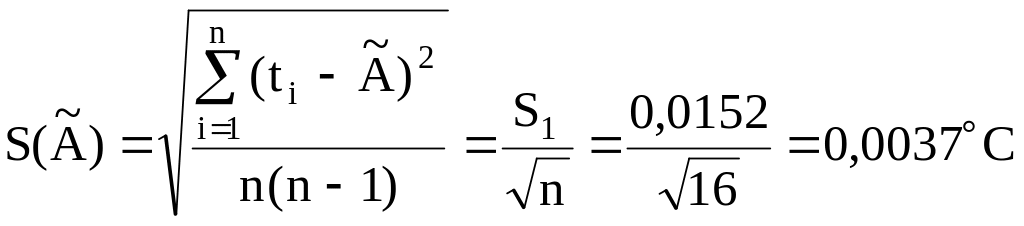Оцінка середнього квадратичного відхилення результату  спостережень вираховується за формулою:

;

Для f=n-1=15 з таблиці 2: M_f=1,017, отже S₁=1,017*0,0037=0,00376C.

Оцінка дисперсії:

незміщена 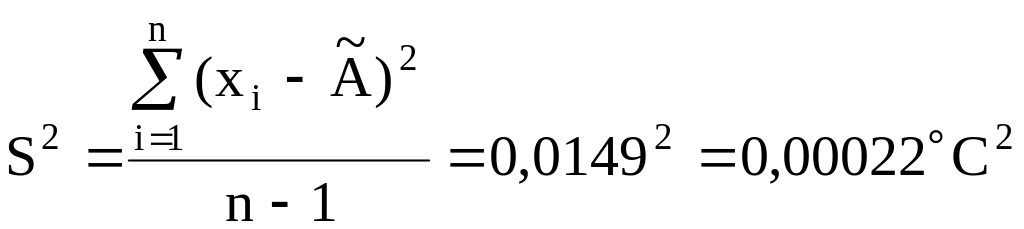4;

зміщена .

3. Перевіримо гіпотезу про те, що результати спостережень належать до нормального розподілу згідно із складовим критерієм.

Критерій 1

Вираховуємо зміщену оцінку середньоквадратичного відхилення результатів вимірювання:

;

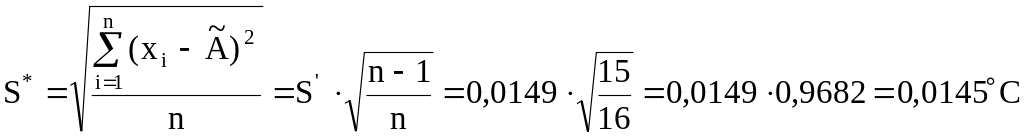Обчислюємо відношення:

.

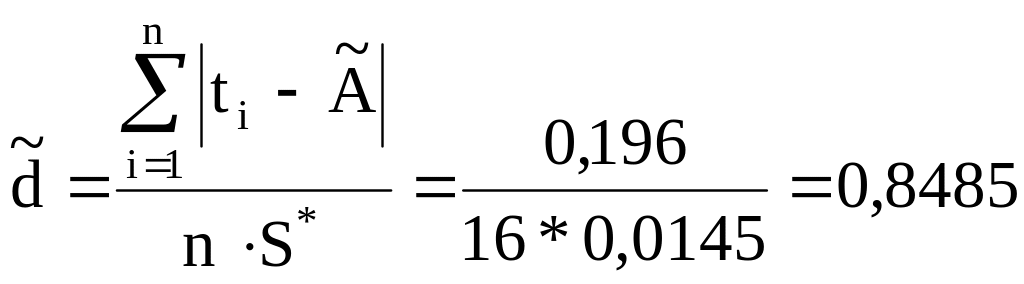З таблиці 3 для n=16 i P=95% отримуємо значення квантілів розподілу ; .

Перевіряємо виконання умови: ,

0,7236 < 0,8485 < 0,8884

Умова виконується, отже робимо висновок, що результати спостережень згідно з критерієм 1 розподілені нормально.

Критерій 2

Незміщена оцінка середнього квадратичного відхилення .

З таблиці 4 для n=16 i q₂=5% (Р_Д=95%) отримуємо m=1; P=0,98;

Знаходимо верхній квантіль розподілу нормованої функції Лапласа при p/2=0,98/2=0,49.

Для Ф_о(z)=0,4900 знаходимо .

Допустиме значення різниці .

Кількість різниць, яка перевищує значення повинна бути .

Найбільша з різниць дорівнює .

Як бачимо жодна з різниць не перевищує значення 0,0346С. Отже результати спостережень згідно з критерієм 2 розподілені нормально.

Оцінки центральних моментів розподілу другого m₂, третього m₃ і четвертого m₄ порядків вираховуються за формулами:

;

; .

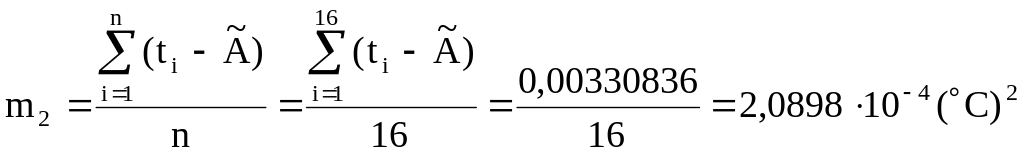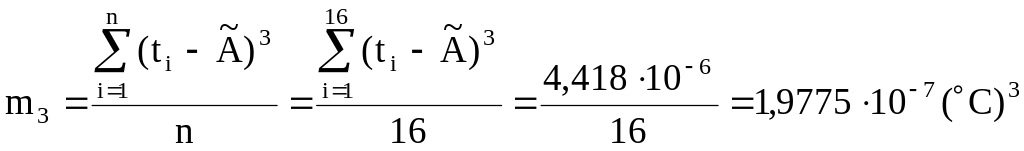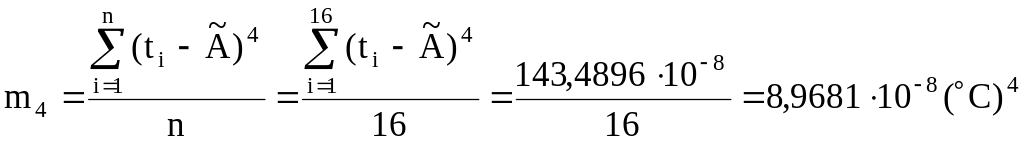Оцінки характеристик асиметрії і ексцесу (гостро- чи плосковершинності) розподілу, які позначаються відповідно і , дорівнюють:

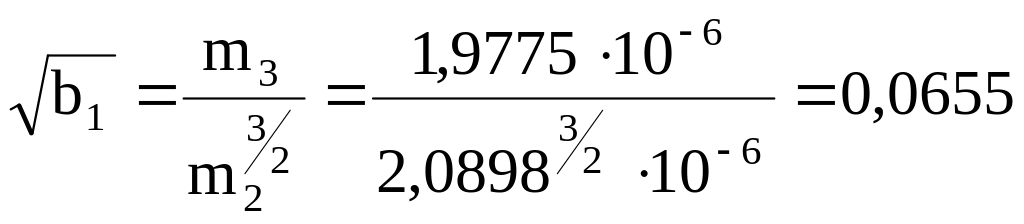>0 асиметрія додатна, розподіл правосторонній

<3 розподіл плосковершинний.

Методика Пірсона:

Для того, щоб перевірити з допомогою методики Пірсона, чи результати вимірювань належать до нормального розподілу, додатково необхідно вирахувати дисперсії характеристик асиметрії та ексцесу D(b₂), які відповідно визначаються:

і перевірити виконання наступних умов:

;

;

;

.

Як бачимо ці умови виконуються, отже робимо висновок що результати вимірювань належать до нормального розподілу.

4 Випадкова складова похибки результату вимірювання визначається за формулою:

.

де t – коефіцієнт Ст’юдента.

За таблицею 5 для заданих числа f=n-1=15 ступеня вільності та довірчої ймовірності P_д=95% знаходимо .

Отже .

Таким чином результат вимірювання температури запишеться: .