2. Колмогоров – Смирнов келісім белгісі.

«Х» кездейсоқ шаманы бақылауда алынған таңдамалар х₁,х₂,…,х_n болсын. Кездейсоқ шама «Х»-нің үлестірім заңы белгілі болғандағы «Н₀» болжамы тексеріледі.

Бұл белгідегі есептеуде теориялық және бақыланатын үлестірімнің арасындағы айырмашылығы ретінде υ_i бақыланатын жиілік және теориялық жиілік арасындағы айырмашылықтың ең үлкен абсолюттік шамасына сәйкес келетін мән қолданылады: d_max=

Белгінің формуласы: _,

мұндағы N – статистикалық қатардағы бақылау саны.

Маңыздылық денгейі р=0,05 λ_кр=1,36.

Егер _{болса, онда берілген маңыздылық деңгейіңде «Н0» болжамды қайтаруға (жоққа шығаруға) негіз жоқ.}

Егер _{болса, онда берілген маңыздылық деңгейіңде «Н0» болжамын жоққа шығарады және «Н1» болжамын қабылдайды.}

Бақылау саны (көлемі) жеткілікті үлкен (N≥50) болғанда Колмогоров -Смирнов белгісі қолданылады.

t-Стьюдент (Госсет) белгісі – бұл өлшеу саны артқанда, қалыпты үлестірімге жақындайтын үлестірімнің айырмашылығын бағалайтын белгі.

t-Стьюдент белгісі – бұл таңдаманың біртектілігін тексеретін әдіс. Ол екі таңдаманың мәндерінің орташа шамаларының теңдегі туралы болжамды қабылдауға немесе қабылдамауға мүмкіндік береді.

Стьюдент белгісін қолданудың негізгі шарттары:

• қарастырылатын таңдамалылар қалыпты үлестірілген болу керек;

• таңдамалылар дисперсиясы тең болу керек.

Стьюдент белгісі таңдамалылардың саны аз болғанда (n_1,2≤30) қолдануы мүмкін.

t-Стьюдент белгісін қолдануының екі жағдайы:

1. Екі тәуелсіз таңдама мәндерінің орташа шамаларының теңдегі (екі таңдамалы t-белгісі) туралы болжамды тексеруде қолданады.

Бұл жағдайда саны әртүрлі бақыланатын және тәжирібелік таңдамалылар талданады.

2. Екі тәуелді таңдама мәндерінің орташа шамаларының теңдегі (жұпталған t-белгісі) туралы болжамды тексеруде қолданады.

Бұл жағдайда тәжирібеге дейінгі және кейінгі сол таңдама талданады.

Стьюдентің екітаңдамалы t-белгісін қолдану реті:

1. Н₀:

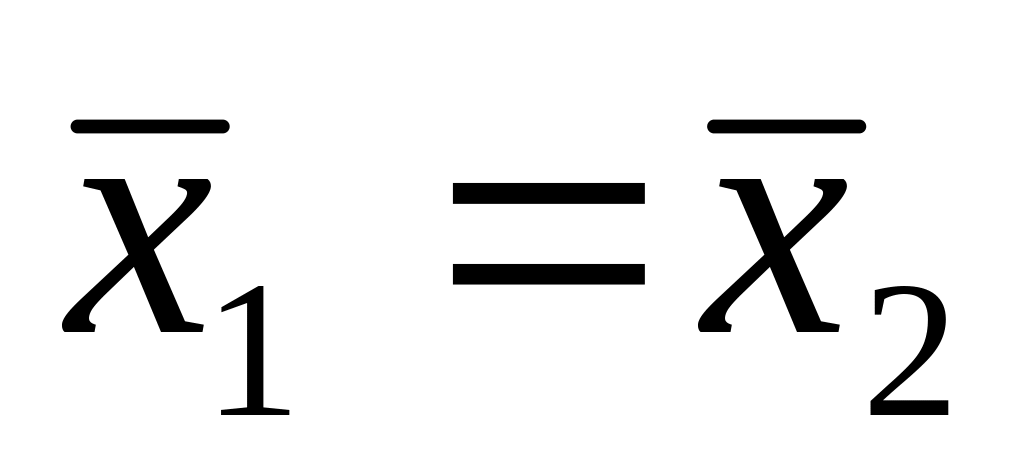
Н₁:

_{2. р=0,05}

_3.

мұндағы n₁, n₂ – қарыстрылатын таңдамалардың көлемі, - қарыстрылатын таңдамалардың дисперсиясы, - салыстырылатын таңдамалылардың орташа, n₁+n₂-1=f - еркіндік дәрежесі.

4. .

5. Егер < болса, онда берілгендердің орташа мәндерінің айырмашылығының статистикалық маңызы жоқ, яғни нөлдік болжам (Н₀: ) қабылданады.

Егер > болса, онда берілгендердің орташа мәндерінің айырмашылығының статистикалық маңызы бар, яғни нөлдік болжам қабылданбайды.

Стьюдентің жұпталған t-белгісін қолдану реті:

2. Н₀:

Н₁:

_{2. р=0,05}

_{3. ,}

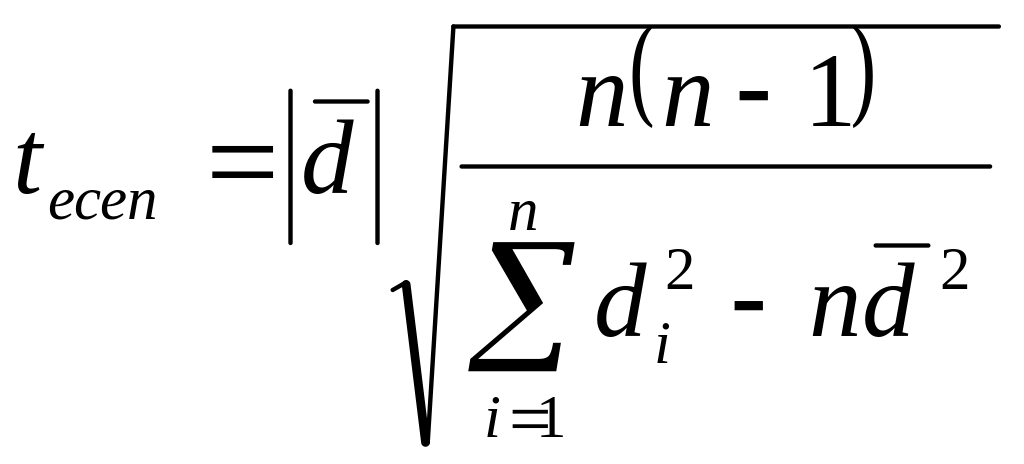мұндағы - сәйкес жұп айнымалылар арасындағы мәндерідің айырымы, - осы айырымының орташа мәні, n – таңдама көлемі, n-1=f - еркіндік дәрежесі.

4. .

5. Егер < болса, онда берілгендердің орташа мәндерінің айырмашылығының статистикалық маңызы жоқ, яғни нөлдік болжам (Н₀: ) қабылданады.

Егер > болса, онда берілгендердің орташа мәндерінің айырмашылығының статистикалық маңызы бар, яғни нөлдік болжам қабылданбайды.

Статистикалық белгі параметрлік және параметрлік емес деп бөлінеді.

Параметрлік белгі – айнымалылар қалыпты үлестірілген деп қарастыратын, аралық немесе қатынас шкалаларында өлшенетін (мысалы, t-Стъюдент, χ² Пирсон белгілері) статистикалық белгі.

Параметрлік емес белгі – талданатын статистикалық үлестірімді функция түрінде қарастырмайтын, олардың қолдануы алдын ала үлестірім параметрлерін есептеуді ұсынбайтын (мысалы, Манна-Уитни, Уилкоксон, таңбалар белгілері) белгі.

Бұл белгілер өздігінен алынған шамаларды емес, олардың орналасу реті (ранг), үлкен-кішілігі бойынша қатынасы саластырады.

Параметрлік емес белгінің қолданылуы параметрлік белгі қарағанда басымырақ болуы, оның негізінен реттілік көрсеткішті (сандық емес) қолданыуында. Бұл әсіресе медицинадағы өлшеулер үшін өте маңызды.

Бұдан басқа параметрлік белгі қалыпты үлестірім қалыбын (формасын) талдауды қажет етпейді, яғни тек қана қалыпты үлестірімге ғана есептелмеген, солай бола тұрса да оның шарттарында сенімді нәтижелер береді.

Математикалық статистикада параметрлік және параметрлік емес белгілер үшін әртүрлі қосымшаларда қуаттылығы төмен немесе қуаттылығы анықталмаған белгілер құрылған.

Сондықтан медициналық қосымшаларда көптеген жағдайларда бірнеше негізгі критерилердің жиынының ішінен салыстырмалы түрде тек қуаты жоғарыларын пайдаланған дұрыс.

4. Иллюстрациялы материалдар: Көрме, слайдтар