Тема: Геометричні тіла. Об'єми та площі поверхонь геометричних тіл

Головні питання:

1. Призми, піраміди, зрізані піраміди, правильні многогран­ники — найпростіші та найважливіші види многогранників.

2. Призмою називають многогранник, у якого дві грані - рівні лі-кутники, а решта п граней - паралелограми. Призма називається прямою, якщо її бічні ребра перпендикулярні до основ. Призма називається правильною, якщо вона пряма, а її основи - правильні многокутники. Площа бічної поверхні прямої призми дорівнює добутку периметра її основи на ви­соту.

3. Паралелепіпедом називають призму, в основі якої лежить паралелограм. Якщо бічні ребра паралелепіпеда перпендику­лярні до площин основ, його називають прямим паралеле­піпедом. Якщо всі 6 граней паралелепіпеда прямокутники, його називають прямокутним паралелепіпедом. Квадрат діа­гоналі прямокутного паралелепіпеда дорівнює сумі квадратів трьох його вимірів. Усі діагоналі прямокутного паралелепі­педа рівні.

4. Пірамідою називають многогранник, одна грань якого - довільний многокутник, а всі інші грані - трикутники, що мають спільну вершину. Піраміда називається правильною, якщо її основою є правильний многокутник, центр якого збі­гається з основою висоти. Висота бічної грані правильної пі­раміди, проведена з її вершини, - апофема піраміди. Площа бічної поверхні правильної піраміди дорівнює добутку півпериметра її основи на апофему.

5. Многогранник називається правильним, якщо всі його грані - рівні правильні многокутники, а всі вершини одна­ково віддалені від деякої точки. Існує всього 5 видів пра­вильних многогранників: правильні тетраедр, гексаедр (куб), октаедр, додекаедр та ікосаедр.

6. Циліндр, конус, зрізаний конус, куля, кульовий сегмент, кульовий сектор - найважливіші тіла обертання.

7. Циліндр - тіло, утворене обертанням прямокутника нав­коло його сторони. Поверхня циліндра складається з двох основ і бічної поверхні. Основи циліндра - рівні круги, що лежать у паралельних площинах; бічну поверхню можна розгорнути у прямокутник. Тому якщо радіус і висота ци­ліндра r і h, то площа його бічної поверхні S = 2 rh, площа поверхні S = 2 r(r + h).

8. Конус - тіло, утворене обертанням прямокутного трикут­ника навколо його катета. Якщо радіус конуса г, а твірна І, то площа бічної поверхні конуса

S = rl,, а площа поверхні

S = r(r + l)

9. Куля - тіло, утворене обертанням круга навколо його діа­метра. Сфера - поверхня кулі; її можна утворити обертан­ням кола навколо його діаметра. Площину (пряму), яка має з кулею тільки одну спільну точку, називають дотичною пло­щиною (прямою) до кулі. Якщо дві сфери мають лише одну спільну точку, то вони дотикаються в цій точці.

10. Об’єм - кількісна характеристика тіла.

11.Кожне тіло має певний об’єм, виражений додатним чис­лом.

12 . Рівні тіла мають рівні об’єми.

13.Якщо тіло поділене на кілька частин, то його об’єм дорів­нює сумі об’ємів усіх цих частин.

14. Об’єми тіл можна вимірювати або обчислювати.

15. Об’єм прямокутного паралелепіпеда дорівнює добуткові трьох його вимірів: V = аbс.

16 . Об’єм призми (і циліндра) дорівнює добутку площі основи на висоту:

V = Об’єм циліндра V = nr²h.

17.Об’єм піраміди (і конуса) дорівнює третині добутку площі основи на висоту: V = 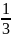Sh. Об’єм конуса V = r² h.

18. Об’єм кулі радіуса г визначається за формулою V = = r³