7.3 Вопросы к защите лабораторной работы №6

1 Что понимается под индексом в статистике?

2 Какова роль индексного метода анализа в экономических исследованиях?

3 По каким признакам классифицируются индексы?

4 Что характеризуют индивидуальные индексы? Приведите примеры.

5 Охарактеризуйте общие индексы.

6 Дайте определение индексируемой величине и весу индекса. Как выбираются веса агрегатного индекса?

7 Запишите формулы общих индексов стоимости продукции, физического объема продукции и цен.

8 В чем состоит различие агрегатных индексов Ласпейраса и Пааше?

9 Что характеризует разность числителя и знаменателя агрегатных индексов физического объема продукции и цен?

10 В каких случаях применяют средние индексы?

11 Запишите формулы средних индексов (арифметических и гармонических) физического объема продукции и цен.

12 Когда применяются системы индексов?

13 Как взаимосвязаны между собой цепные и базисные индексы?

14 Каким образом строятся системы индексов с переменными и постоянными весами?

15 С помощью системы каких индексов характеризуется изменение средней величины индексируемого показателя и факторов, влияющих на его динамику?

16 Запишите формулы индексов переменного и постоянного состава, структурных сдвигов.

17 С какой целью используют территориальные индексы? Запишите формулу территориального индекса цен, построенного методом стандартных весов.

8 Лабораторная работа №7 Статистическое изучение взаимосвязи социально – экономических явлений

8.1 Указания к лабораторной работе №7

В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя корреляционный анализ, а другая - регрессионный анализ.

При оценке тесноты связи между количественными признаками применяется линейный коэффициент корреляции, который характеризует тесноту и направление связи между двумя признаками в случае наличия между ними линейной зависимости.

Данный коэффициент может быть рассчитан по формуле:

.

Линейный коэффициент корреляции изменяется в пределах от -1 до 1. Если значение коэффициента находится в пределах от 0 до 1, то это свидетельствует о наличии прямой связи между признаками, если в пределах от -1 до 0, то – об обратной связи. При связь между признаками отсутствует, если (или ), то связь является функциональной.

Парная линейная регрессия характеризует линейную связь между признаками: результативным и факторным. Аналитически связь между ними описывается уравнением: .

Оценка параметров линейного уравнения регрессии , осуществляется методом наименьших квадратов (МНК), при котором минимизируется сумма квадратов отклонений фактических значений результативного признака от теоретических.

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:

,

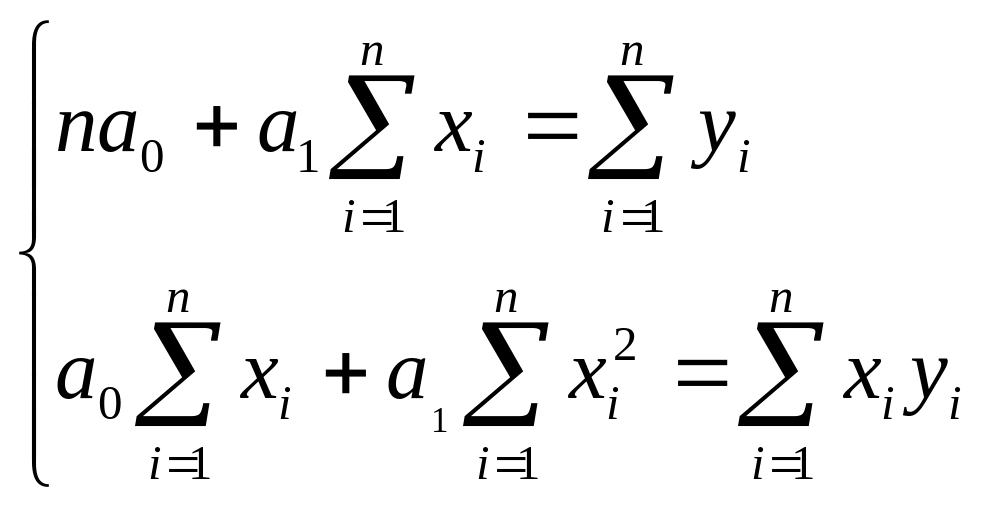где n - объем исследуемой совокупности (число единиц наблюдения).

В уравнении регрессии параметр показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр - коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при изменении факторного на единицу его собственного измерения.

Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю результативного признака, объясняемую регрессией. Чем больше коэффициент детерминации, тем лучше линейная модель регрессии аппроксимирует исходные данные и ею можно пользоваться для прогноза значений результативного признака.

При выполнении заданий лабораторной работы №7 необходимо изучить материал, изложенный в [13, с. 253-260, с. 271-297 и др.].