§ 8.8. Шартты экстремум

1.Шартты экстремум. Айталық, және айнымалылары

₍₁₎

теңдігін қанағаттандыратын болсын. Айнымалылары (1) теңдікті қанағаттандыратын

(2)

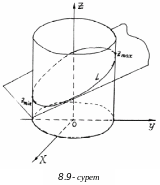
функциясының экстремумын тауып, оны геометриялық тұрғыдан түсіндірейік. Берілген жазықтығымен цилиндрдің қиылысу сызығы (эллипс) бойынша аппликатаның ең үлкен және ең кіші мәндерін табу (8.9-сурет).

Бұл есепті шешу үшін алдымен (1) теңдіктен тауып (2) теңдікке қоямыз:

. (3)

Сонымен, (1) шартты қанағаттандыратын (2) функцияның экстремумын табу бір ғана - тен тәуелді болатын (3) функцияның экстремумын табуға келіп тіреледі. Бұл функцияның анықталу аймағы кесіндісі болады. Егер Вейерштрасс теоремасын еске алсақ, (3) функцияның экстремумы бар екендігі анық. Бұл қарастырылған есеп, функциясының аргументтері белгілі бір байланыста болатын шарттарды қанағаттандырған кездегі функциясының экстремумдарын табу мақсатына арналған есептің дербес жағдайы болып табылады. Сондықтан да,  мақсаттық функция деп аталады.

Сонымен, айнымалылары

(8.43)

байланыста болған кездегі ,

(8.44)

мақсаттық функцияның экстремумын табу жөніндегі есепті қарастырамыз. Мұндағы (8.43) теңдеулер жүйесі байланыс шарттары деп аталады.

Егер (8.43) байланыс шарттарын қанағаттандыратын нүктесі үшін маңайы табылып, осы маңайда жататын барлық нүктелері үшін

(8.45)

қатынасы орындалатын болса, онда (8.44) мақсаттық функцияның жергілікті шартты максимум (минимум) нүктесі деп аталады.

2. Лагранждық көбейткіштер тәсілі. Айталық, (8.43) байланыс шарттарын қанағаттандыратын және осы нүктедегі 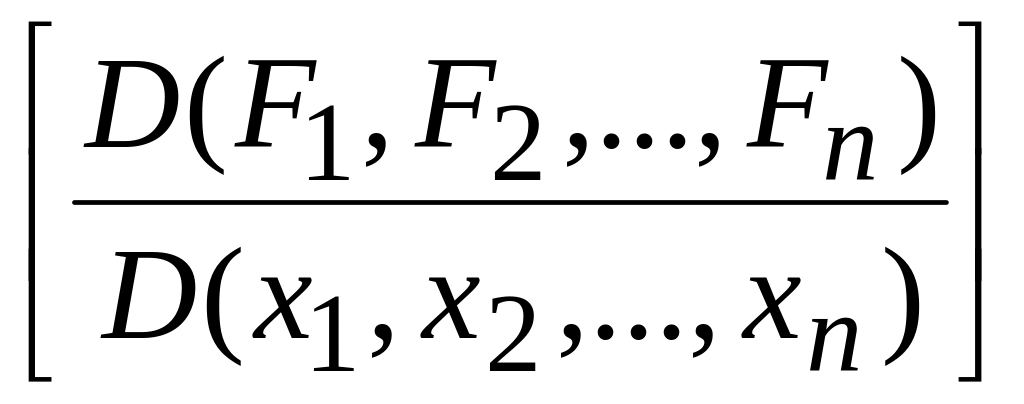Якоби матрицасының рангы болсын. Бұл кезде бұл матрицаның - ші ретті миноры

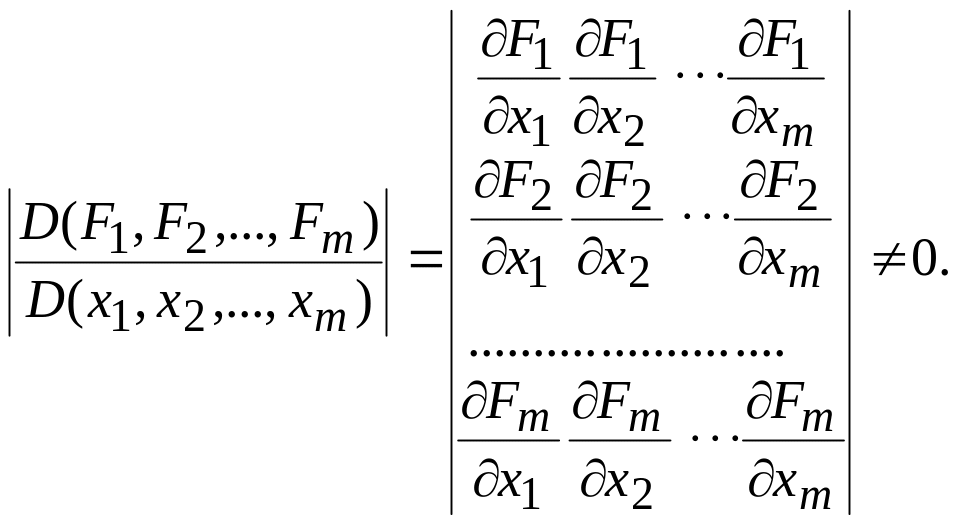(8.46)

Онда (8.65) теңдеулер жүйесінен айнымалыларын, қалған айнымалыларының функциялары ретінде өрнектеуге болады.

Енді мынадай көмекші функция құрайық,

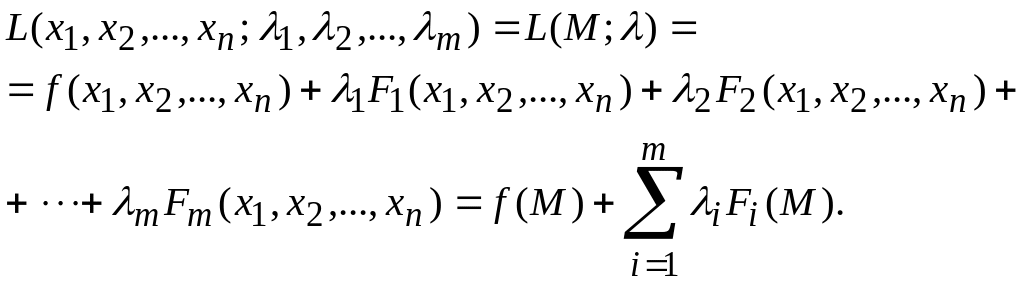(8.47)

Мұндағы  кейбір сандар. Осы алынған (8.69) Лагранж функциясы деп аталады, ал сандары арқылы құралған Лагранж көбейткіштері деп аталады.

8.13. Теорема. (Шартты экстремум болудың қажетті шарттары). Айталық, функциялары (8.43) байланыс шарттарын қанағаттандыратын нүктесінің маңайында үзіліссіз дифференциалданатын болсын. Егер функциясының нүктесінде экстремумы бар және 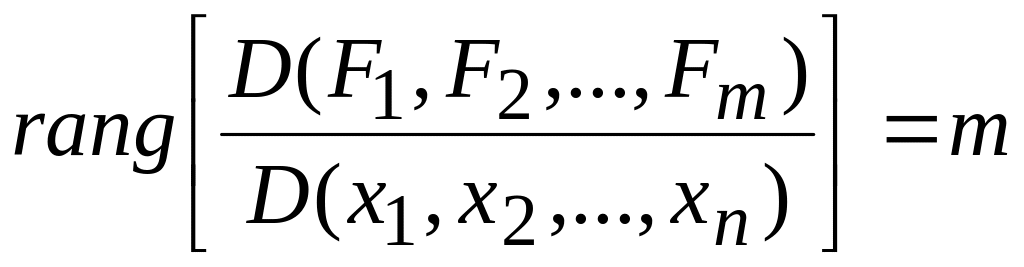болса, онда сандары табылып, болғанда,

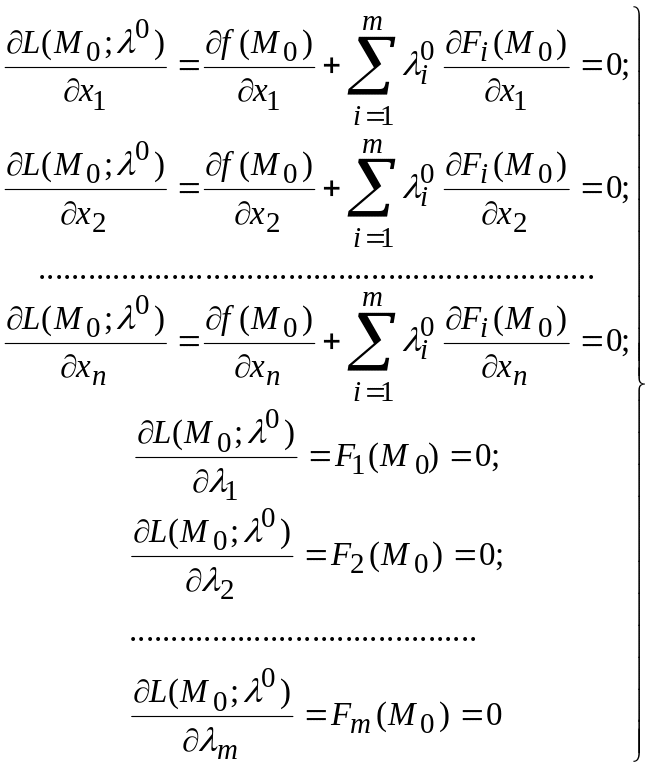(8.48)

теңдіктері орындалады.

Бұл теореманың дәлелдеуін келтірместен, жоғарыдағы мәселелердің барлығын байланыс шартын қанағаттандыратын, екі айнымалы, функциясы үшін жергілікті шартты экстремум болудың қажетті шартын ғана келтірейік.

Сонымен, Лагранж функциясының түрі болса, онда

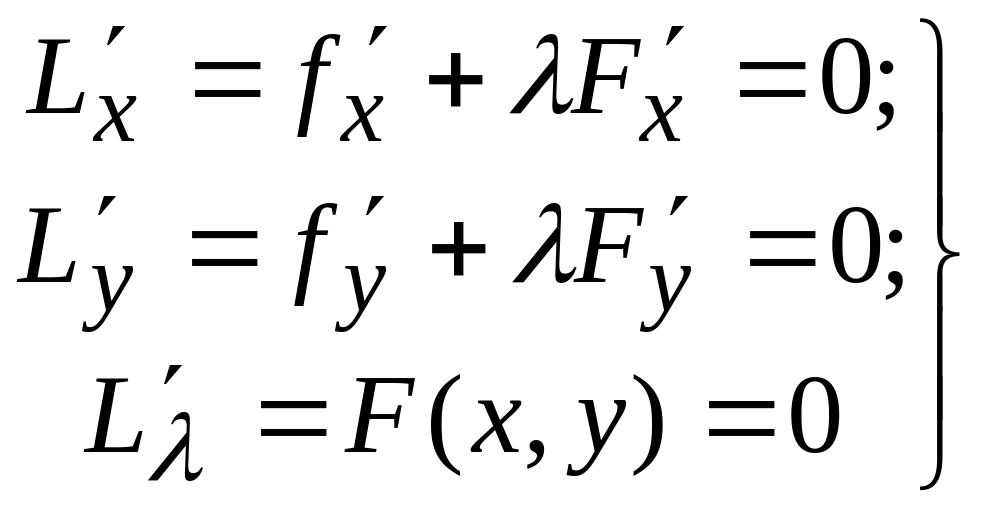(8.48^¢)

теңдіктері орындалады.

Жоғарыдағы ) шарттарды қанағаттандыратын(8.48) немесе (8.48’) нүктесі (8.47) Лагранж функциясының (8.43) байланыстағы стационар нүктесі ) теңдеулер жүйесін шешу  деп аталады. Ол нүкте (8.48) немесе (8.48’) арқылы анықталады.

8.14. Теорема. (Шартты экстремум болудың жеткілікті шарты). Егер  Лагранж функциясына сәйкес , функциялары, нүктесі маңайында, екі рет үзіліссіз дифференциалданатын, және

(8.49)

қатынастары орындалатын болса, онда байланыста болатын функциясының нүктесінде жергілікті шартты максимумы (минимумы) болады.

Бұл теореманың да дәлелдеуін келтірместен, (8.49) шарттарға пара-пар, дербес туындылар арқылы шартты экстремум болудың жеткілікті шарттарын келтірейік.

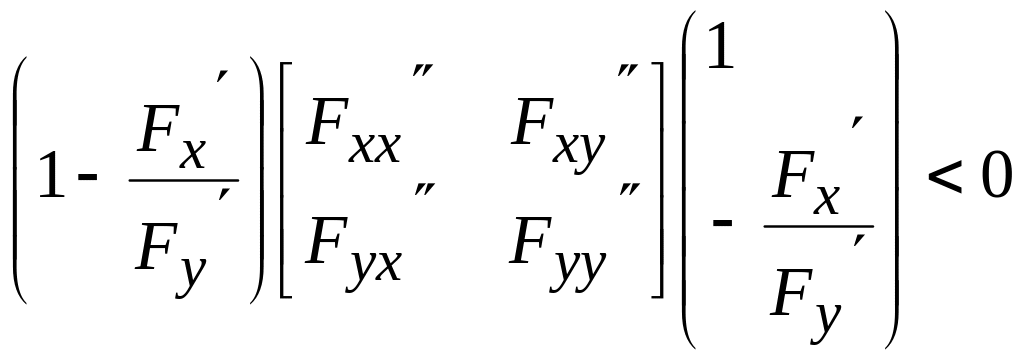
 шартты максимум;

(8.50)

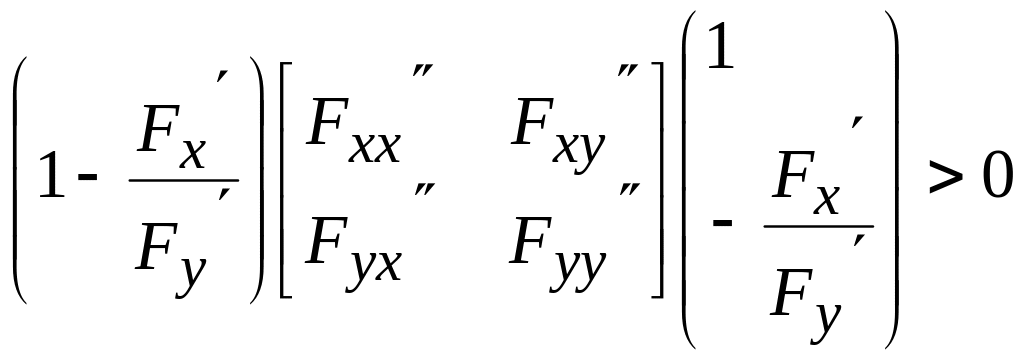
 шартты минимум.

М.23^*. байланыс шартын қанағаттандыратын функциясының шартты экстремумдарын табайық.

Шешуі. Сәйкес Лагранж функциясы

болады. Онда (8.48) немесе (8.48’) бойынша:

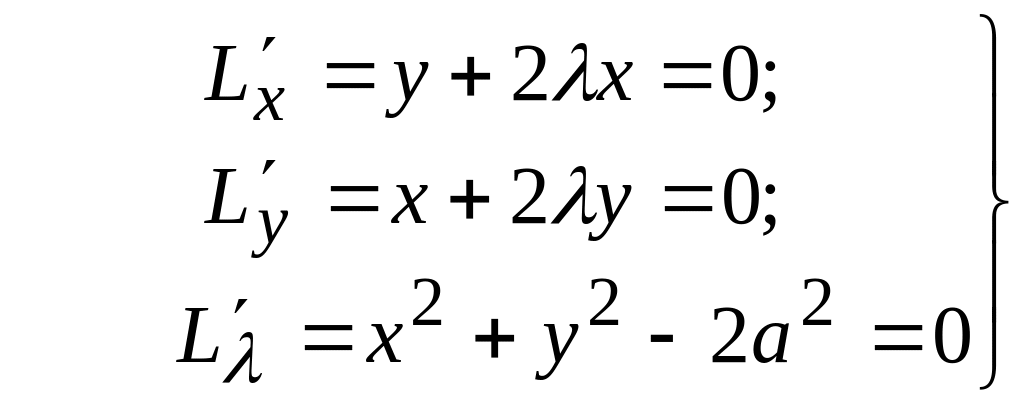
теңдеулер жүйесін шешу арқылы функциясының мүмкін болатын шартты экстремум немесе стационар нүктелерін анықтаймыз.

Сонымен, Осы нүктелердегі (8.73) - дің таңбаларын анықтайық.

 нүктесінде функциясы өзінің жергілікті шартты максимумын қабылдайды, яғни .

Сол сияқты, . Демек, және нүктелерінде жергілікті шартты минимумдар  ; нүктесінде жергілікті шартты максимум  мәндерін қабылдайды.

Ескерту. Жоғарыдағы формулаларды және

байланыста болатын  үш айнымалы функция үшін келтірейік.

Егер  Лагранж функциясы үшін стационар нүктеде

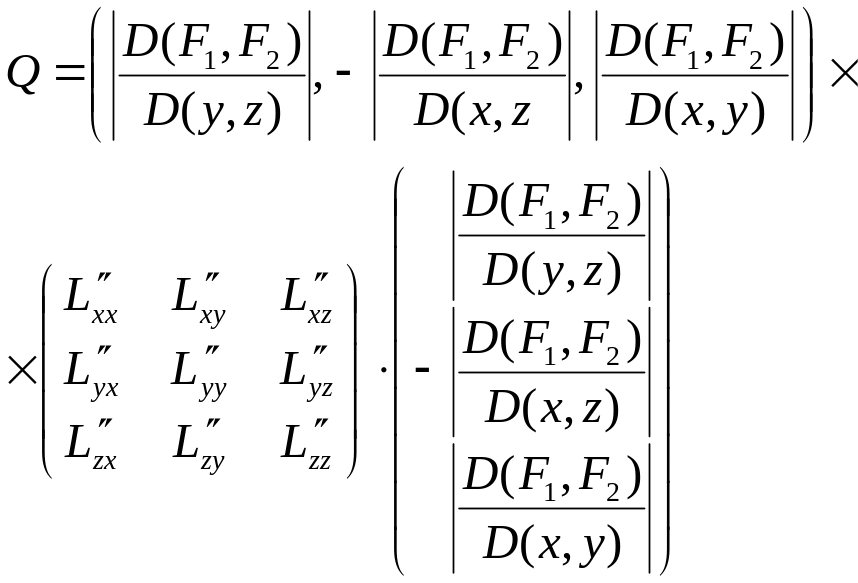(8.51)

матрицасы оң (теріс) анықталған болса, онда функциясының нүктесінде жергілікті шартты минимумы (максимумы) болады.

М.24^*. Берілген жазықтықтары арқылы анықталған түзудің бойында және бас нүктеге жақын орналасқан нүктесін табайық.

Шешуі. Есептің шарты бойынша кесінді квадратының минимумын табуымыз керек, яғни айнымалылары және байланыс шарттарын қанағаттандыратын

функциясының кіші мәнін табу керек.

Ол үшін

(1)

Лагранж функциясын құрып,

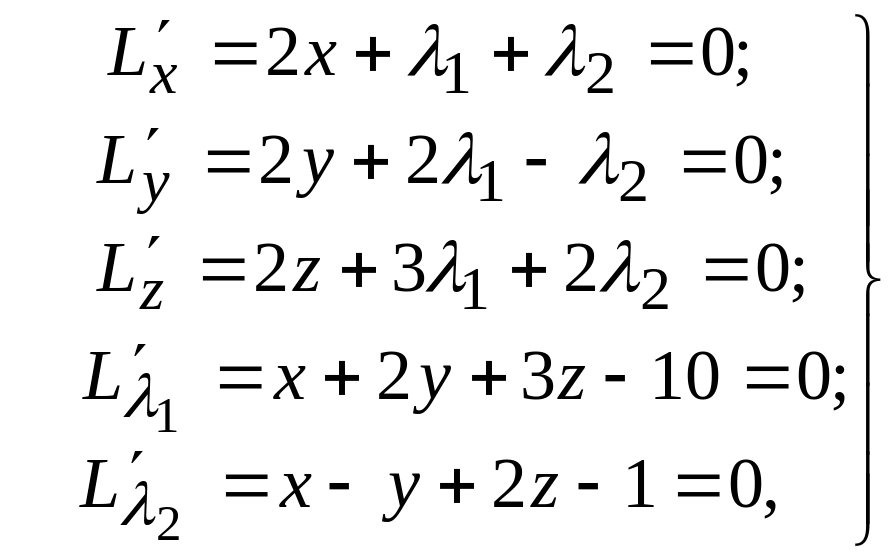(2)

теңдеулер жүйесін шешу арқылы (1) функциясының стационар нүктелерін табамыз.

Сонымен,

Енді және жазықтықтары арқылы анықталатын түзудің бойында жатқан нүктесінің бас нүктеден арақашықтығы ең аз болатындығына көз жеткізейік. Ол үшін нүктесіндегі Якобиандар мен матрицаны есептейік:

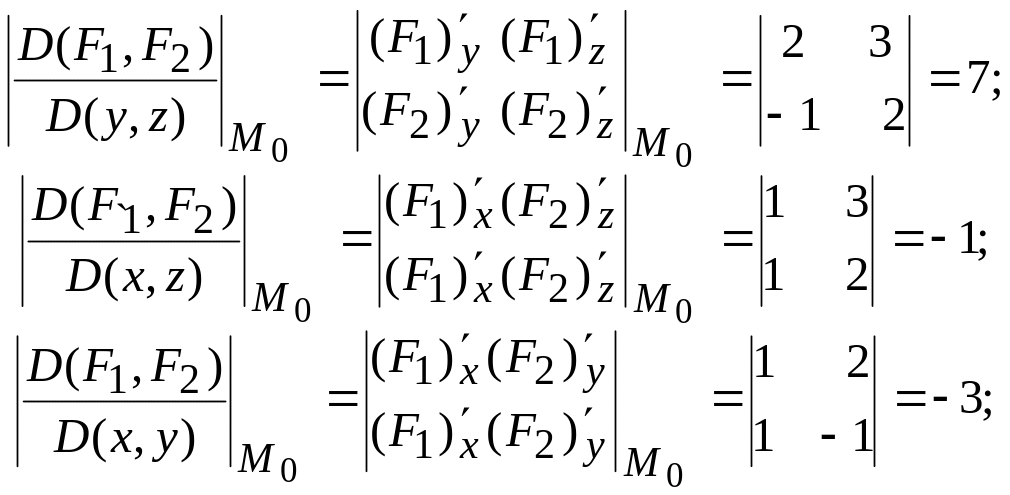(3)

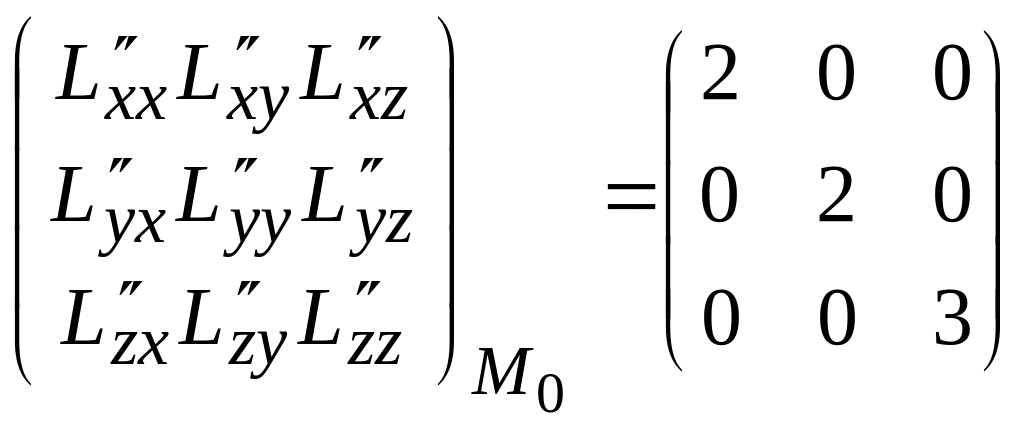(4)

Алынған (3) және (4) өрнектерді пайдаланып, (8.51) матрицасын құрып, оның оң немесе теріс анықталғандығын тексереміз. Сонымен,

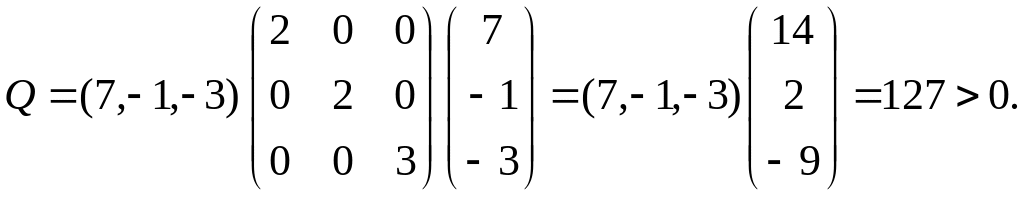
Демек, оң анықталған. Ендеше, (8.49) шарты экстремумның жеткілікті шарты бойынша, функциясы нүктесінде өзінің жергілікті шартты минимумын қабылдайды. Ендеше нүктесі бас нүктеге ең жақын орналасқан нүкте болып табылады.