§ 8.7. Көп айнымалы функциялардың экстремумдары
1.
Экстремумның қажетті шарттары. Айталық,
функциясы
'
жиынында анықталған болсын. Егер
нүктесінің
маңайында жататын кез келген
нүктесі үшін
(8.36)
қатынасы орындалатын болса, онда функциясы нүктесінде өзінің жергілікті минимумын (максимумын) қабылдайтын болады.
Егерде
(8.37)
қатынасы орындалатын болса, онда берілген функция нүктесінде өзінің жергілікті қатаң минимумын (максимумын) қабылдайтын болады. Мұндағы берілген функцияның қатаң экстремум нүктесі деп аталады.
8.11. Теорема. (Экстремум болудың қажетті шарттары). Егер дифференциалданатын функциясының нүктесінде жергілікті экстремумы бар болса, онда
(8.38)
теңдіктері орындалады.
Жоғарыдағы
(8.38)
теңдіктерін қанағаттандыратын
'
жиынында
жататын
нүктелері, функцияның стационар
нүктелері
деп те аталады.
2. Экстремумның жеткілікті шарттары. Айталық, функциясының екінші ретті қоса есептегенде үзіліссіз дербес туындылары бар болсын.
8.12. Теорема. (Экстремумның жеткілікті шарттары). Айталық, екі рет үзіліссіз дифференциалданатын функциясының стационар нүктесі болсын. Егер
(8.57)
қатынасы орындалатын болса, онда берілген функциясының нүктесінде жергілікті минимумы (максимумы) болады.
Сонымен, берілген функциясының нүктесінде жергілікті экстремумы болуының жеткілікті шарттары ретінде:
Егер:
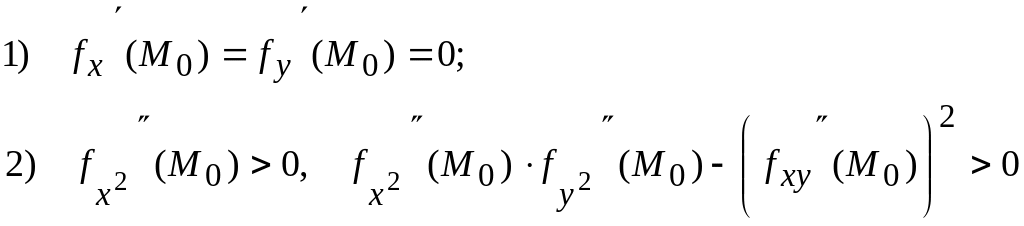(8.39)
болса, жергілікті минимумның жеткілікті шарттары; ал
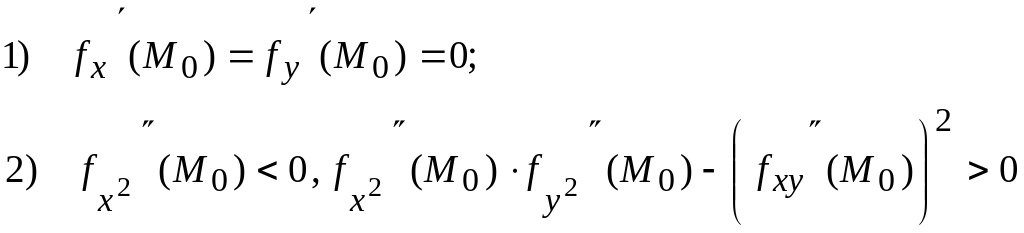(8.40)
болса, жергілікті максимумның жеткілікті шарттары болып табылады.
Егерде
(8.41)
болса, берілген функцияның нүктесінде экстремумы жоқ.
М.20*.
функциясын экстремумға зерттейік.
Шешуі. Экстремум болудың қажетті шарттарын пайдаланып
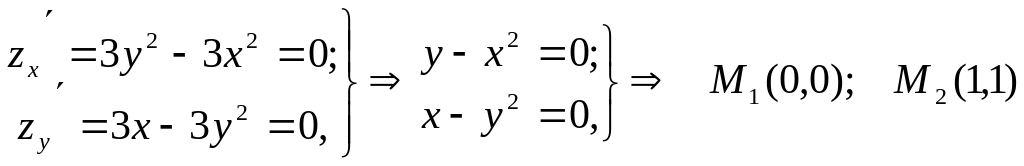
стационар нүктелерді табамыз.
Енді Гессе матрицасын құрайық:
Жоғарыдағы
(8.39)
және (8.40)
формулалары бойынша табылған
және
нүктелеріндегі Гессе матрицасының оң
немесе теріс анықталғандығын зерттейміз.
нүктесінде
(8.41)
шарт бойынша берілген функцияның
экстремумы жоқ.
нүктесінде
матрицасы теріс анықталған. Демек, бұл
нүктеде функцияның жергілікті максимумы
бар және ол
.
М.21*.
функциясын
экстремумға зерттейік.
Шешуі. Қажетті шарттарды пайдаланып стационар нүктелерді табайық:
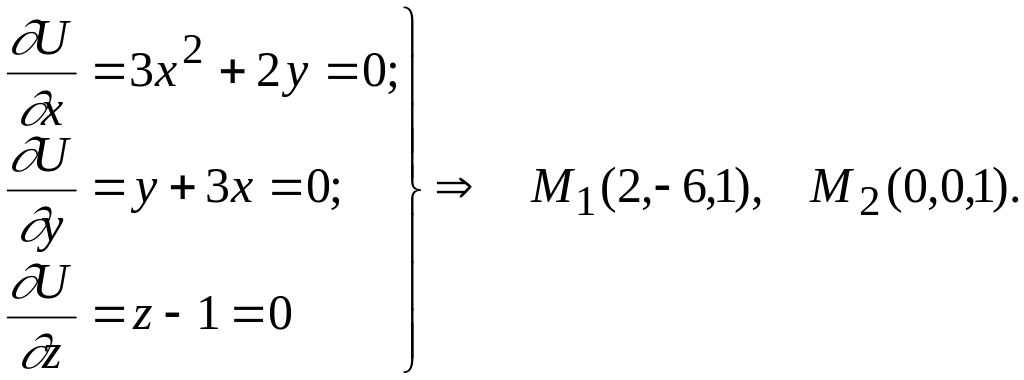
Енді Гессе матрицасын құрайық, яғни
Бұдан
нүктесінде:
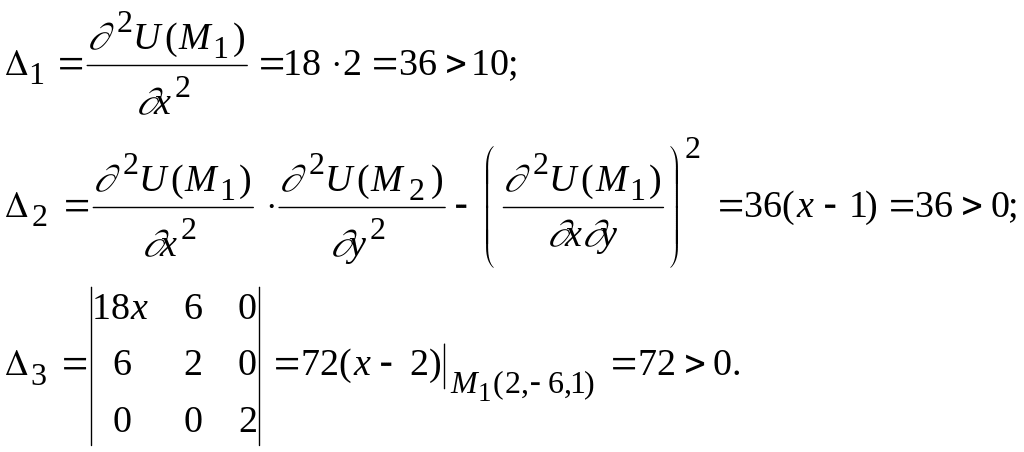
Бұл
нүктеде берілген функцияның жергілікті
минимумы бар, яғни,
Ал
нүктесінде
Демек, (8.41)
шарт бойынша экстремум жоқ. Екінші
жағынан,
Бұдан
нүктесінің өте аз маңайында функцияның
мәні әрі оң, әрі теріс болады. Шынында
да, егер
болса,
Демек,
нүктесінде экстремум жоқ.
Ескерту.
теңдеуінен шығатын айқындалмаған
функциясы үшін экстремум болудың қажетті
шарттары ретінде
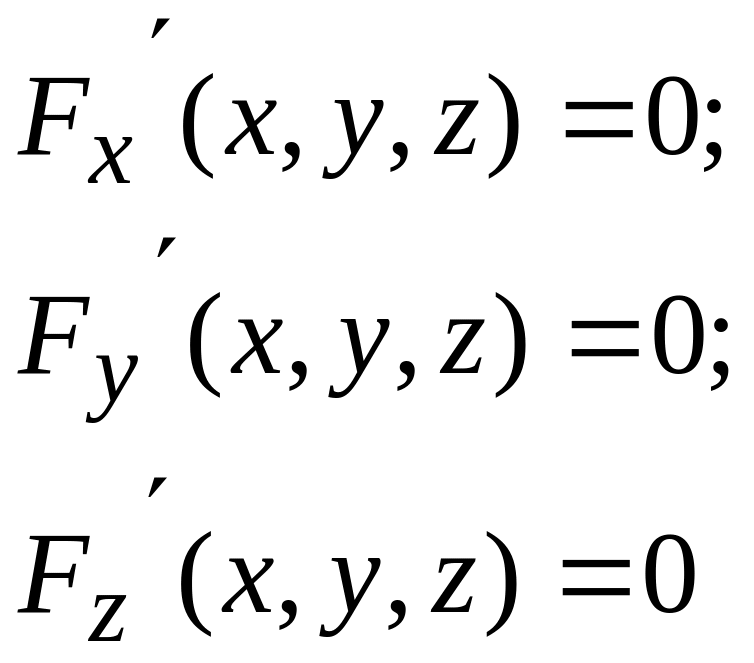(8.42)
теңдеулер жүйесін алуға болады. Ал экстремумның сипатын (түрін) анықтау үшін жоғарыдағы келтірілген жеткілікті шарттарды пайдалануға болады.
3.
Тұйық аймақтағы функцияның ең үлкен
және ең кіші мәндері. Айталық,
функциясы
бетімен шектелген
тұйық аймағында анықталған, үзіліссіз
және осы аймақтың барлық ішкі нүктелерінде
дифференциалданатын болсын. Онда
Вейерштрасс теоремасы бойынша функцияның
анықталу аймағынан
және
нүктелері табылып, функция өзінің ең
үлкен және ең кіші мәндерін (жалпы
экстремум) қабылдайды, яғни
Мұндағы
және
нүктелері
функциясының анықталу аймағында жататын
стационар нүктелерінің ішінде немесе
шекарада жатқан нүктелер арасында жатуы
мүмкін. Сонымен, функцияның жергілікті
экстремумдары мен шекаралық нүктелердегі
экстремумдарды салыстыру арқылы, олардың
ішіндегі ең үлкені және ең кішісі,
қажетті функцияның
ең үлкен және ең кіші
мәндері ретінде алынады.
М.22*.
функциясының,
түзулері арқылы берілген үшбұрыш бойынша
ең үлкен және ең кіші (жалпы экстремум)
мәндерін табайық (8.8-сурет).
Шешуі. Берілген үшбұрыш ішінде жатқан стационар нүктелерді іздейік.
Осы
нүктедегі берілген функцияның мәнін
есептейміз, яғни
.
Үшбұрыштың
,
қабырғаларында функция мәндері
.
Енді үшбұрыштың
қабырғасы, яғни
түзуі бойындағы функцияның ең үлкен
және ең кіші мәндерін анықтаймыз. Ол
үшін
теңдеуін пайдалансақ, берілген
бір айнымалы функцияға айналады. Демек,
ендігі мақсатымыз
кесіндісінде жатқан
функциясының жергілікті экстремумдарын
табу.
Шеткі
нүктелерінде функция нөльге тең.
;
Мұндағы
-
шеткі
нүкте. Ал
.
Сонымен,
берілген
функциясының жалпы экстремумын:
функция мәндері ішінен таңдаймыз, яғни
