§ 8.5. Жоғарғы ретті дербес туындылар

және дифференциалдар

1. Жоғарғы ретті дербес туындылар. Егер функциясының дербес туындылары дифференциалданатын болса, онда олардың берілген аргументтер бойынша дербес туындыларын табуға болады.

Сонымен, болса, онда

(8.29)

берілген функциясының сәйкес айнымалылары бойынша екінші ретті дербес туындылары деп аталады.

Дәл осы сияқты дербес туындылардан екінші ретті дербес туындыларды да табуға болады 

.

Осылайша, егерде екінші ретті дербес туындылар дифференциалданатын функциялар болса, онда үшінші ретті дербес туындыларды, әрі қарай жалғастыра беруге болады. Егерде дербес туындылар дифференциалданатын болса, онда функцияларынан сәйкес бойынша дербес туындылар табу арқылы, ретті дербес туындыларды алуға болады.

М.15^*. функциясы үшін, дербес туындыларын табайық.

Шешуі. Тізбектеп дербес туындыларды табуға кірісейік.

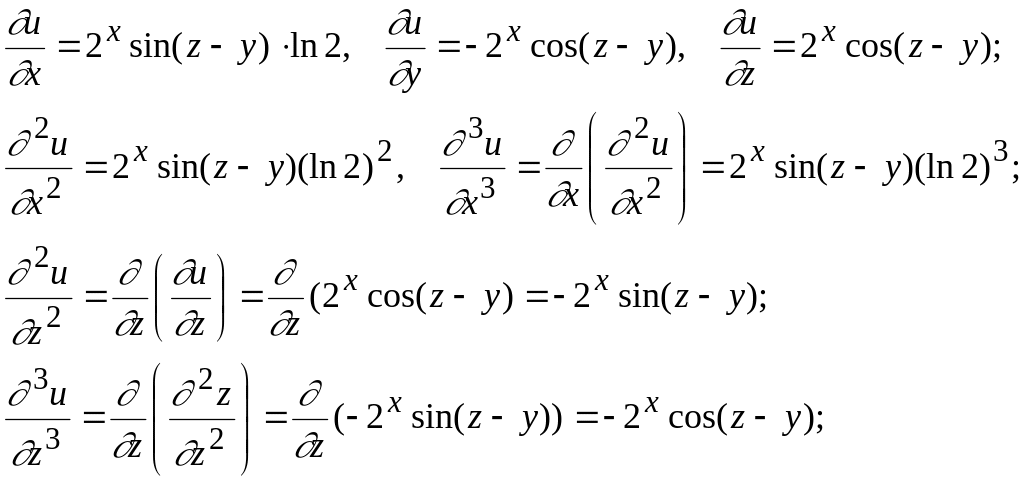
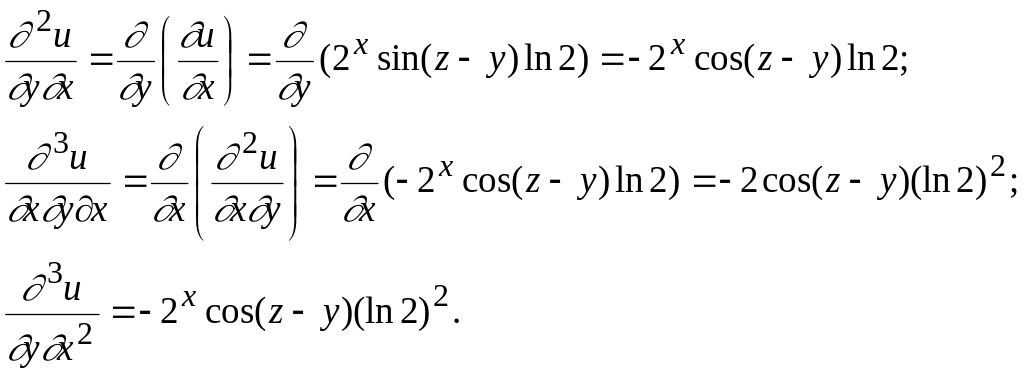
Бұл мысалдан болатындығын көреміз.

8.8. Теорема. Егер функциясының нүктесінде екінші ретті аралас дербес туындылары бар болса, онда

(8.30)

теңдігі орындалады.

Ескерту. 8.8-теореманы негізге ала отырып, кез келген ретті аралас дербес туындылар үшін:

т. с. с. теңдіктерді алуға болады.

2. Жоғарғы ретті дербес дифференциалдар. Айталық, функциясының кез келген ретті үзіліссіз дербес туындылары бар болса, онда оның толық дифференциалы

(1)

теңдігімен анықталады және ол шын мәнінде  төрт айнымалы функция болып шығады. Осы (1) функцияның дифференциалын, берілген функциясының екінші дифференциалы жөнінде сөз қозғайық. Бұл кезде функциясынан және айнымалылары бойынша дербес туынды алған кезде және тұрақты ретінде қарастырылады 

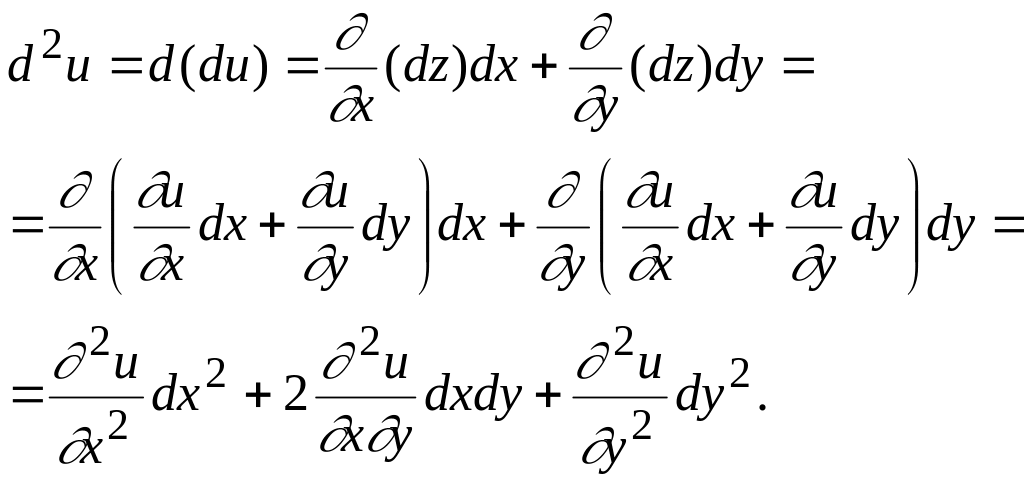(8.31)

Мұндағы (8.8- теорема) және .

Дәл осы сияқты,

.

§ 8.8. Aйқындалмаған функциялар

1. Aйқындалмаған функция ұғымы. Оны дифференциалдау

Ендеше, функцияның айқындалмаған түрін пайдаланып, тепе-теңдігін алуға болады.

Сонымен, теңдеуінен, қандай шарттарды қанағаттандырған кезде, оны (немесе ) арқылы шешуге болатындығын көрсетейік.

8.9. Теорема. Айталық, функциясы нүктесі маңайында үзіліссіз дифференциалданатын болсын. Егер:

à)

. (8.33)

болса, онда нүктесінің белгілі бір маңайы табылып, теңдеуін арқылы шешуге болады, яғни нүктесінің маңайында жататын кез келген және үшін тепе-теңдігін қанағаттандыратын функциясы табылады.

Енді теңдеуімен анықталған, айқындалмаған функцияның дифференциалдануын қарастырайық.

Айталық,  үзіліссіз дифференциалданатын және болсын. Онда 8.8- теорема бойынша теңдеуінен айқындалмаған, үзіліссіз дифференциалданатын функциясын табуға болады және оның туындысы,

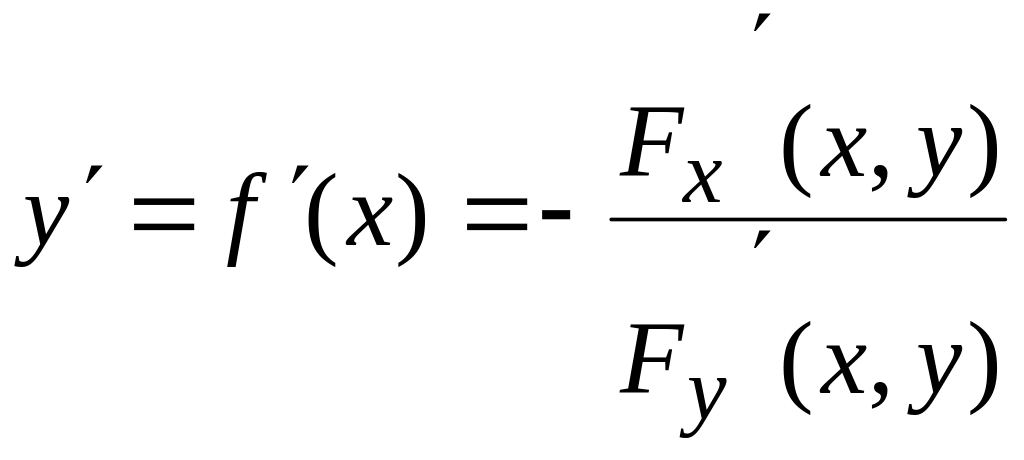(8.34)

теңдігімен анықталады. Шынында да, (8.25)  функцияның толық туындысы формуласы бойынша, тепе-теңдігінен

Бұдан (8.51) формула шығады. Егерде үзіліссіз дифференциалданатын болса, онда

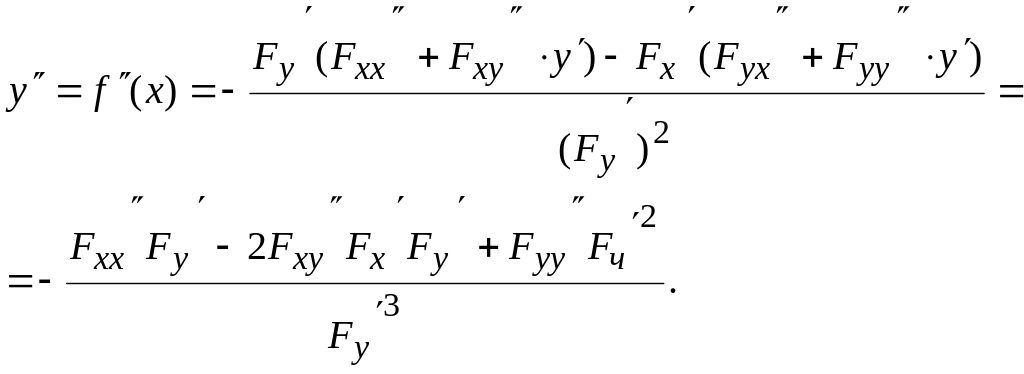(8.35)

Дәл осы сияқты, тізбектеу арқылы т.с.с. жоғарғы ретті туындыларды табуға болады.

М.17^*. теңдеуі бойынша айқындалмаған функциясының туындысын табайық.

Шешуі. Мысалдың берілуі бойынша . Онда . Демек, (8.34) формула бойынша,

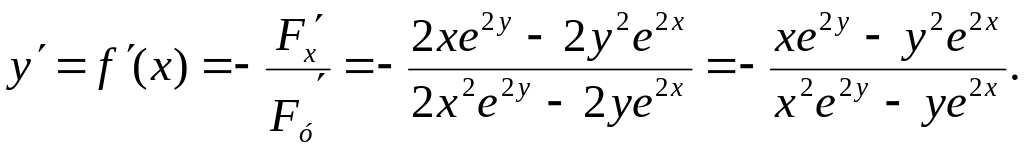
М.18^*. теңдеуі арқылы берілген қисыққа нүктесінде жүргізілген жанама мен нормальдың теңдеуін жазайық.

Шешуі. Жанама мен нормальдың теңдеулері өзара ортогональ және . Ендеше, (8.34) формула бойынша, олардың сәйкес теңдеулерін аламыз.

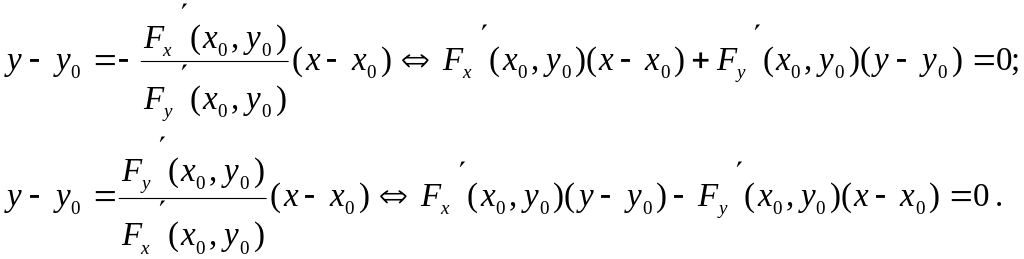
2. Бір теңдеу арқылы анықталған, айқындалмаған функция. Өткен пункттегі сияқты айқындалмаған көп айнымалы функция теңдеуі арқылы беріледі. Қарастыруға жеңілірек болу үшін, теңдеуі арқылы анықталған,  екі айнымалы функцияны қарастырайық.

8.10. Теорема. Айталық, функциясы нүктесі маңайында үзіліссіз дифференциалданатын болсын. Егер:

а) ә)

болса, онда теңдеуін арқылы бір мәнді етіп шешуге болатын нүктесінің -маңайын табуға болады, яғни нүктесінің маңайы және үзіліссіз дифференциалданатын бір ғана функциясы табылып, маңайында жататын кез келген нүктелері және үшін тепе-теңдігі орындалады.

Бұл кезде функциясының дербес туындылары:

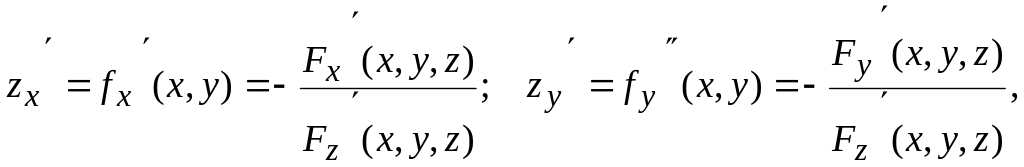(8.53)

теңдіктерімен анықталады.

М.19^*. теңдеуінің нүктесі маңайында болатын бір ғана шешімі болатындығын көрсетейік. Осы шешімнің берілген нүктелердегі дербес туындыларын табайық.

Шешуі. функциясы нүктесінде үзіліссіз дифференциалданады және а) ә) яғни 8.9-теорема шарттары орындалады. Демек, теңдеуі үшін нүктесінде болатын бір ғана функциясы табылады. Ал оның нүктесіндегі дербес туындылары: