Енді (8.22) формула бойынша
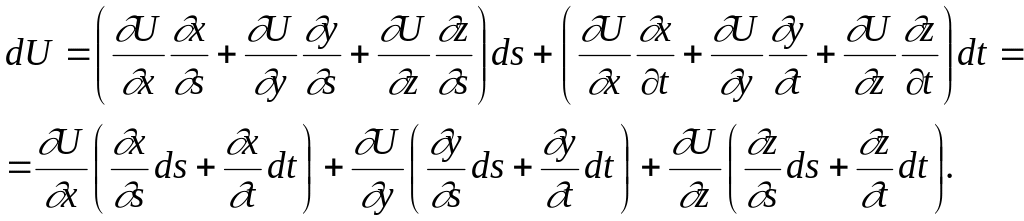(2)
Мұндағы,
болғандықтан,
(2) теңдіктен
(3)
түрі
бойынша (8.28) формулаға ұқсас теңдік
алдық. Бірақ, ол теңдікте
тек тәуелсіз айнымалылар
шамаларының дифференциалдары, ал (3)
теңдіктегі
екі айнымалы функциялардың дифференциалдары.
Демек, (8.23) және (3) теңдік түрі жағынан
бірдей болғаны мен мағыналары жағынан
әртүрлі.
Бірінші дифференциалдың осы қасиетін, оның инварианттық түрі деп атайды.
§ 8.4. Бағыт бойынша туынды. Градиент
1.
Бағыт бойынша туынды. Жазықтықта
немесе кеңістікте жатқан кез келген
бағыты
бірлік векторымен анықталады. Мұндағы
бағытымен сәйкес Оx,Оy,Оz
координаталар өстері арасындағы бұрыш
(8.4-
сурет).
А
йталық,
функциясы, радиус - векторы
болатын
нүкте-сінің
-маңайында
анықталған болсын (суретке қара).
1. Егер
(1)
шегі
бар болса,
онда ол шек
функциясының
нүктесіндегі
бағыты бойынша алынған туынды деп
аталады және
немесе
түрінде белгіленеді.
Сонымен, анықтама бойынша,
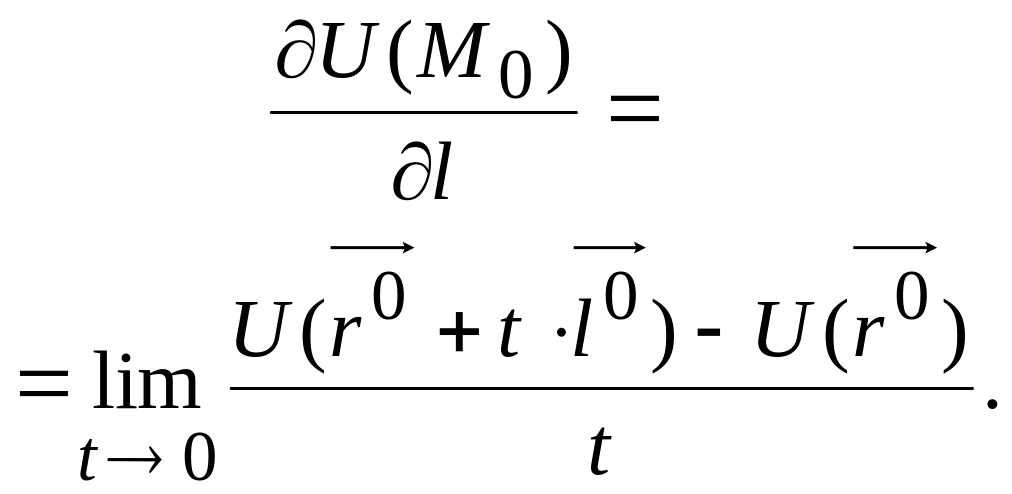(8.23)
Енді бағыт бойынша туындының координаталық түрін қарастырайық. Ол үшін нүктесінен шығатын бағытының координаталарын жазайық (8.4- сурет)
(2)
Онда
.
(3)
Ендеше, (8.28) формула бойынша
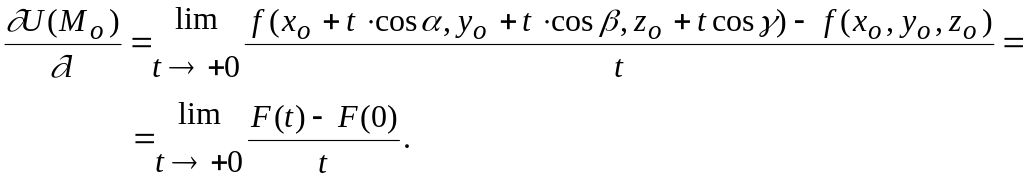(4)
Демек, (8.23) туынды, (4) туындымен бірдей. Егер нүктесінде үзіліссіз дифференциалданатын болса, онда (8.26) формула бойынша, кеңістігінде
(8.24)
теңдігін аламыз.
М.10.
кеңістігінде жатқан дененің температурасы
функциясы
арқылы берілген болсын. Осы дененің
нүктесінен бас нүктеге қарай тараған
температура өзгерісінің жылдамдығын
табайық.
Шешуі.
Берілген бағытқа сәйкес бірлік вектор
-
болады.
Онда
Ал
Демек, температураның таралу жылдамдығы, (8.24) формула бойынша
8.8.
Теорема. Егер
функциясы
үшін
болса,
онда
бағыты бойынша берілген функция
нүктесінде қатаң
өсетін (кемитін) болады.
М.11.
функциясынан,
винттік
сызығы
бойымен
нүктесінде
алынған
туындыны
табайық.
Шешуі. Жанама вектордың координаталарын табайық.
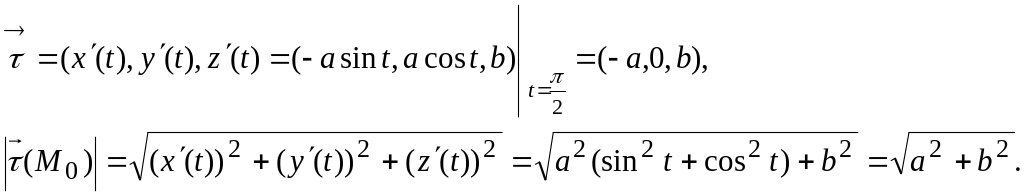
Онда (8.31) формуланы пайдаланып,
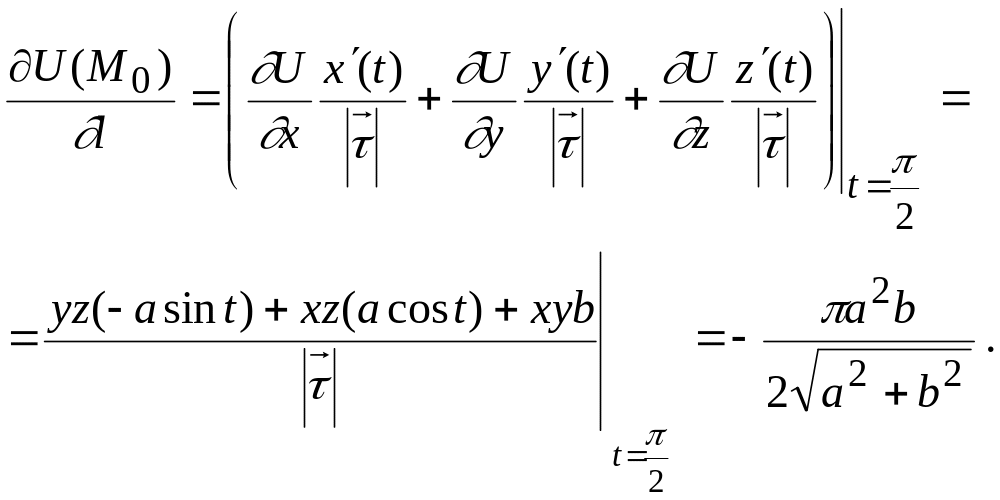
2.
Функция градиенті. Дифференциалданатын
функциясының
нүктесіндегі градиенті
деп,
координаталары
болатын
векторды айтамыз және grad
немесе
түрінде белгілейміз. Сонымен, анықтама
бойынша
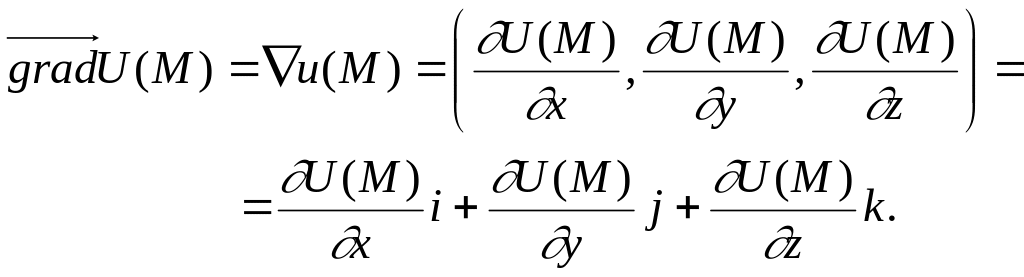(8.25)
Онда бағыты бойынша алынған туынды мен градиент арасындағы байланыс
(8.26)
теңдігімен
беріледі, яғни
бағыты бойынша алынған туынды, функцияның
grad
және
бағытының
бірлік
векторларының скаляр көбейтіндісіне
тең. Ал
болғандықтан,
(8.27)
мұндағы
(8.5-
сурет).
Сонымен,
берілген бағыт
бойынша туынды
деп, дифференциалдау бағытына түсірілген
градиенттің проекциясын айтамыз. Егер
grad
болса,
бағыты
функция градиентімен бағыттас
болғанда,
өзінің ең үлкен (max)
мәнін қабылдайды. Бұл кезде, (8.34) теңдіктен,
градиент бағытымен алынған
функциясының
нүктесіндегі туындысы
(8.28)
теңдігімен анықталады.
Ал grad векторына қарама-қарсы бағытта өзінің ең кіші (min) мәнін қабылдайды.
М.12.
Кеңістіктегі заттың таралу тығыздығы
функциясы арқылы берілген болсын.
нүктесінен
қай бағытта тығыздықтың өзгеру жылдамдығы
тез болады? Берілген нүктедегі тығыздықтың
өзгеру жылдамдығын табайық.
Шешуі.
Жоғарыдағы көрсетілгендей, ең жоғарғы
функция градиентімен бағыттас болады.
Сондықтан
.
Мұндағы
Онда
Демек,
заттың тығыздығының ең үлкен жылдамдықпен
таралуы
векторымен бағыттас және оның шамасы,
(8.28)
формула бойынша,
болады.
Егер
бағыты
векторымен
бағыттас болса, онда оған сәйкес бірлік
вектор
болады, (8.27)
формула
түрін
қабылдайды.
Егер
векторы берілген нүктеде
бетке жүргізілген жанама векторға
перпендикуляр болса, онда
векторы
бетке тұрғызылған нормаль
деп аталады (8.6-
сурет).
8.7.
Теорема. Берілген
функцясының
нүктесіндегі
векторы,
осы функцияға сәйкес
беттік
(сызықтық) деңгейге перпендикуляр
болады.