VIII. Көп айнымалы функциялар
XIV - ДӘРІС
§ 8.1. Жазықтықтағы және кеңістіктегі жиындар
1.
Нүктенің маңайы.
кеңістігіндегі
және
екі
нүкте
арақашықтығы,
(8.1)
теңдігімен
анықталады. Егерде
болса
-
жазықтықты
береді де,
жазықтықтағы
және
(
нүктелерінің арақашықтығын, ал
болғанда,
-
кеңістікті
береді де,
кеңістіктегі
және (
)
нүктелерінің арақашықтығын береді.
Сонымен, берілген екі нүктенің
арақашықтығымен анықталатын
жиыны,
метрикалық
кеңістігі
деп аталады.
Егер
кеңістігінен
ортонормалданған базис және О (бас)
нүктесін алатын болсақ,
және
декарттық координаталар жүйесінің
жалпы түрі саналатын,
координаталар жүйесін аламыз. Бұл кезде
кеңістігінде
жататын
және
векторларының
скаляр көбейтіндісі
, (8.2)
ал
векторының
нормасы
(ұзындығы)
(8.3)
теңдіктерімен анықталады.
Айталық,
нүкте
болсын.
Онда
нүктесінің
-маңайы
деп, арақашықтығы
болатын,
жиынында жататын
нүктелер жиынтығын айтады және
әдеттегідей,
түрінде белгіленеді. Сонымен, анықтама
бойынша,
=
(8.4)
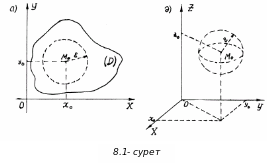Бұл
(8.4) теңдікті қанағаттандыратын, радиусы
-ға
тең, кіндігі
болатын нүктелер жиынтығы
(8.1-сурет),
өлшемді
шар деп
аталады. Егерде маңайға
нүктесінің өзі енбейтін болса, яғни
(немесе
)
нүктесінің ойық
-маңайы
деп аталады.
§ 8.2. Көп айнымалы функциялар
1.
Көп айнымалы функциялар ұғымы. Айталық
кеңістігінде жататын
жиыны берілсін. Егер
жиынында жататын, әрбір
нүктесіне, белгілі бір
заңы бойынша,
саны
сәйкес келетін болса, онда
жиыны бойынша
функциясы
анықталған деп
аталады. Мұндағы
жиыны
функциясының анықталу
аймағы,
саны
нүктесіне сәйкес функцияның дербес
мәні,
ал дербес мәндер жиынтығы функцияның
мәндер
жиыны
деп аталады.
Оған бірнеше мысал келтірейік.
1.
екі айнымалы функция. Оның анықталу
аймағы
кіндігі бас нүктеде жататын, радиусы
-ге
тең дөңгелек (
),
функцияның өзгеру аймағы немесе мәндер
жиыны
(
кесіндісі).
М.1.
функциясының анықталу аймағын
көрсетейік.
Шешуі. екі айнымалы функция. Оның анықталу аймағы,
(1)
шартты
қанағаттандыратын жазық-тықтағы,
яғни
кеңіс-тігіндегі
нүктелер жиыны. Бұл теңсіздік
а)
(2)
ә)
(3)
теңсіздіктер
жүйелеріне пара-пар. Осы теңсіздіктер
жүйелерін шешу арқылы берілген функцияның
анықталу аймағын табамыз. Сонымен, (2)
жүйеден
және
жоғарғы жарты жазықтық пен радиусы
-ге
тең, кіндігі бас нүктеде орналасқан
жоғарғы жарты шеңбердің сырты екендігін
көреміз. Ал (3) жүйеден төменгі жарты
жазықтықтан, төменгі жарты шеңбермен
бөлінген аймақты аламыз (8.2-
cурет).
2.
Нүктедегі функцияның шегі. Айталық,
функциясы D
нүктесінің ойық маңайында анықталған
болсын. Егер кез келген
саны үшін
саны табылып, кез келген
D
нүктесі үшін
болғанда
(8.7)
қатынасы орындалатын болса, онда
саны
функциясының
кездегі шегі
деп аталады және
,
(8.8)
түрінде жазылады.
Осы анықтаманы квантор тілінде берейік:
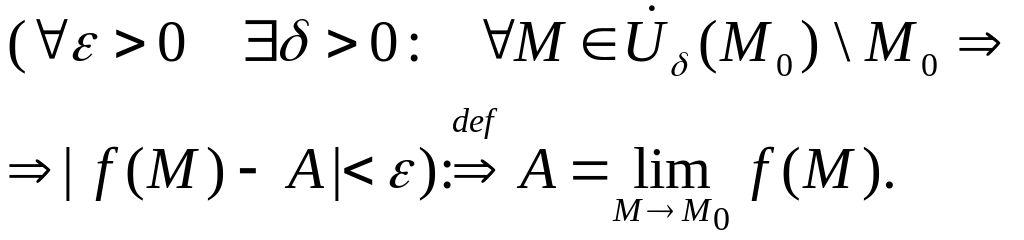
М.2.
функциясының
нүктесіндегі шегін табайық.
Шешуі. Берілген функция, нүктесінен басқа, жазықтықтың барлық нүктесінде анықталған. Сондықтан, нүктесіне бірнеше бағытта жақындайық.
1.
нүктесіне Ох
өсі бойымен, яғни
болсын. Онда
Дәл
осы сияқты, Оу
өсі бойымен, яғни
2.
нүктесі
нүктесіне
түзулері бойымен ұмтылатын болсын.
Мұндағы
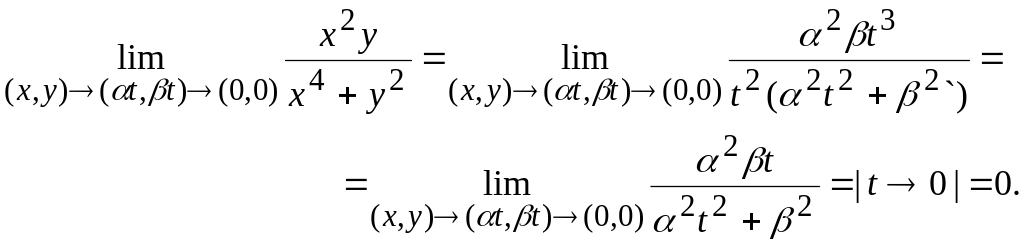
Демек,
бас нүкте арқылы өтетін кез келген түзу
бойымен
кезде, берілген функцияның шегі
;
3.
Енді
нүктесі
нүктесіне, бас нүкте арқылы өтетін қисық
бойымен ұмтылатын болсын. Айталық,
болса, Онда 
Ендеше,
берілген
функциясының
кездегі шегі жоқ (функция әртүрлі шекке
ұмтылады, яғни шектің жалғыздығы туралы
1
қасиет орындалмайды).
Берілген
функциясының
нүктесіндегі шегін басқаша берейік. Ол
үшін, функцияның
және
айнымалыларының біреуі, мысалы,
-
тің
-
ге қалай
ұмтылатындығынан тәуелсіз, екіншісі
тек қана барлық
нүктелері берілген функцияның
анықталу аймағында жатуы міндетті.
Демек, уақытша
-
ті
тұрақты түрінде қарастырсақ,
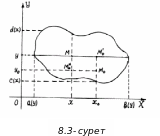
функциясы
болатын бір айнымалы функцияға айналады
(8.3-
сурет).
Онда, алынған бір айнымалы функцияның
шегі
(1)
теңдігімен
анықталып,
-
тен
тәуелді функция болып шығады. Бұл кезде
D
нүктесі
түзуінің бойымен
нүктесіне ұмтылады.
Енді
екінші айнымалы бойынша, яғни
кезде,
шекке
көшсек
(2)
теңдігін аламыз. Бұл кезде нүктесі түзуі бойымен нүктесіне ұмтылатындығын көреміз.
Дәл осы сияқты бірінші айнымалыны уақытша тұрақты деп алып, екінші айнымалыдан бастасақ, (1) теңдік сияқты,
(3)
теңдігін
аламыз. Бұл кезде, алдымен
нүктесі
түзуі бойымен
нүктесіне, соңынан
нүктесі
түзуі бойымен
нүктесіне ұмтылады
(8.3-сурет).
Сонымен,
нүктесінің
нүктесіне ұмтылуы қабырғалары координат
өсьтеріне параллель болатын
тік төртбұрышы бойынша алынған (2) және
(3) теңдіктер, яғни
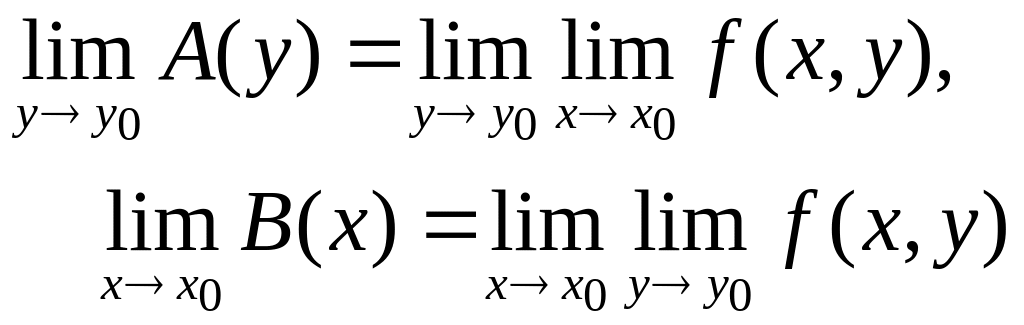(8.9)
қайталанбалы шектер деп аталады.
Ескерту.
Қайталанбалы
шектер ылғи да тең бола бермейді. Мысалы
үшін,
функциясының
нүктесіндегі шегін қарастырайық
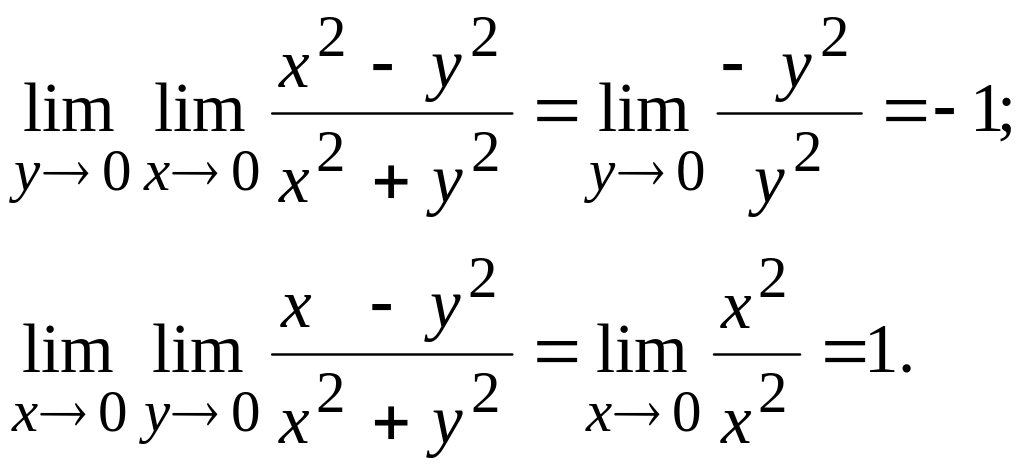
8.2.
Теорема. Егер
еселі шек бар және кез келген
(немесе
)
үшін
шегі бар болса, онда функцияның
,
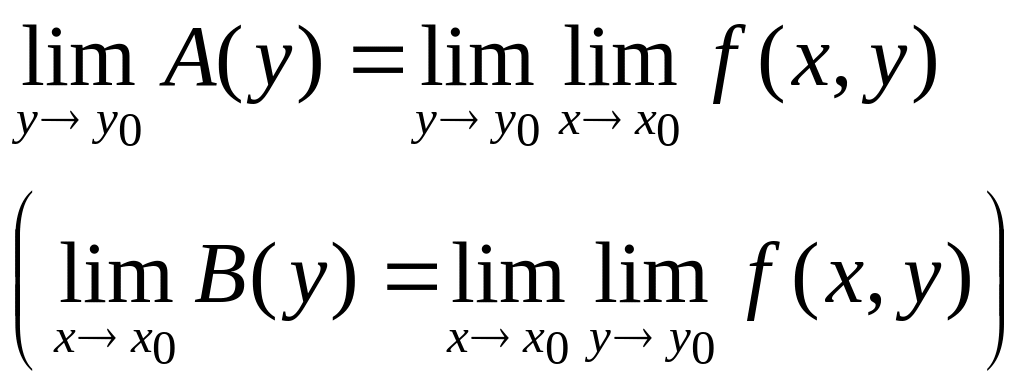қайталанбалы шегі бар және ол шек санына тең.
Енді көп айнымалы функциялар шегінің кейбір қасиеттерін атап өтейік сонымен бірге олардың бір айнымалы функциялар шегінің қасиеттеріне ұқсас екендігін көреміз.
1.
Егер
болса:
а)
ә)
(8.10)
б)
2.
Егер
функциясының
нүктесінде шегі бар болса, онда
нүктесінің
маңайында берілген
функциясы шектелген.
3.
Егер
болса, онда
нүктесінің
маңайы
табылып, сол маңайда жататын кез келген
нүктелері үшін
болады.
3.
Көп айнымалы функциялардың үзіліссіздігі.
1.
Егер
функциясының нүктесіндегі шегі,
функцияның сол нүктедегі мәніне тең,
яғни
(8.11)
болса, онда берілген функция нүктесінде үзіліссіз деп аталады.
2.
Егер кез келген
саны үшін,
саны табылып,
барлық нүктелері үшін
шарты орындалғанда,
(8.12)
теңсіздігі
орындалатын болса, онда берілген
функциясы
нүктесінде үзіліссіз
деп
аталады.
Ескерту. Көп айнымалы функциялардың келтірілген үзіліссіздік анықтамалары, барлық айнымалылар жиынтығы бойынша үзіліссіздік болып табылады.
Айталық,
нүктесіне сәйкес әр айнымалы бойынша
өсімшелерін енгізейік. Бұл кезде
функциясы үшін алынған
(8.13)
теңдігі
нүктесіндегі берілген
функциясының толық
өсімшесі
деп аталады. Ал
(8.14)
берілген функциясының, сәйкес және айнымалылары бойынша дербес өсімшелері деп аталады.
М.3.
функциясының әрбір айнымалы бойынша
нүктесінде үзіліссіз, яғни Ох
және
Оу
координаталар өсі бойында үзіліссіз,
ал бас нүкте арқылы өтетін басқа түзулер
бойында үзіліссіз бола алмайтындығын
көрсетейік.
Шешуі.
1.
Айталық,
нүктесі
нүктесіне Ох
немесе Оу
өсьтері бойынша ұмтылатын болсын, яғни
немесе
.
Онда
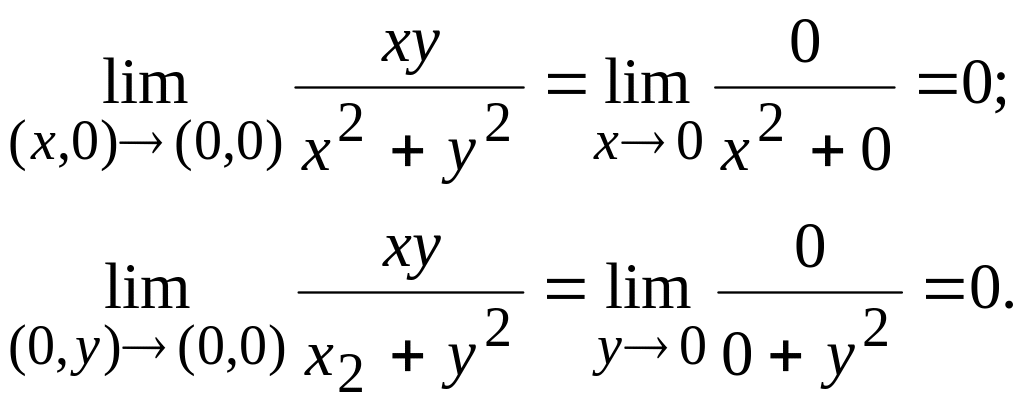(1)
Демек, координаталар өсі бойынша, берілген функция үзіліссіз.
2.
Енді
нүктесі
нүктесіне
түзуі бойымен ұмтылатын болса,
(2) Бұдан
берілген функцияның
нүктесіндегі дербес мәнімен (
-ге
тең) (2) шектің мәні әртүрлі екендігін
көреміз, яғни (8.15) теңдік орындалмайды.
Демек, ол нүктеде функция үзілісті.
Егер
функциясы
тұйық жиында
үзіліссіз болса, онда ол
жиынында шектелген және осы жиында
жататын
және
нүктелерінде өзінің ең
үлкен және ең
кіші мәндерін
қабылдайды.
Егер кез келген
саны үшін, тек қана
-
нан тәуелді болатын
саны табылып,
шартын қанағаттандыратын функцияның
анықталған аймағында жататын
және
нүктелері үшін
(8.15)
теңсіздігі
орындалатын болса, онда
функциясы
D(
)жиынында
бірқалыпты
үзіліссіз
деп аталады.