2. Довжина берегової лінії. Фрактальна розмірність. Поняття фрактала.

При вивченні географії [17, 19]кожна з країн має свою площу території і довжину межі, зокрема, якщо країна омивається яким-небудь морем або океаном, то вона має морську межу певної довжини. Чи замислювалися ви коли-небудь, як цю довжину межі визначають? У 1977 р. американський математик Бенуа Мандельброт поставив перед собою наступне питання: чому рівна довжина берегової лінії Великобританії? Виявилось, що коректно відповісти на це "дитяче питання" не вдається. У 1988 р. норвезький учений Енс Федер вирішив з'ясувати, чому рівна довжина берегової лінії Норвегії. Звернете увагу на те, що побережжя Норвегії сильно порізане фіордами. Інші учені ставили собі аналогічні питання про довжини берегових ліній побережжя Австралії, Південної Африки, Німеччини, Португалії і інших країн.

Ми можемо зміряти довжину берегової лінії тільки приблизно. У міру того як ми зменшуємо масштаб, нам доводиться вимірювати все більше маленьких мисів і бухт - довжина берегової лінії збільшується, і об'єктивної межі зменшенню масштабу (і, тим самим, збільшенню довжини берегової лінії) просто не існує; ми вимушені визнати, що ця лінія має нескінченну довжину. Ми знаємо, що розмірність прямої лінії рівна одному, розмірність квадрата - двом, а розмірність куба - трьом. Мандельброт запропонував використовувати для вимірювання "жахливих" кривих дроби розмірності - розмірності Хаусдорфа - Безіковіча. Нескінченно зламані криві, подібні до берегової лінії, - не цілком лінії. Вони як би "замітають" частину площини, подібно до поверхні. Але вони і не поверхні. Значить, резонно припустити, що їх розмірність більше одного, але і менше двох, тобто це розмірні для дробу об'єкти.

Норвезький учений Е. Федер, запропонували інший спосіб вимірювання довжини берегової лінії. Карту покрили квадратною сіткою, осередки якої мають розміри е ? е. Видно, що число N(e) таких осередків, які покривають берегову лінію на карті, приблизно рівне числу кроків, за яке можна обійти по карті берегову лінію циркулем з розчином e. Якщо е зменшувати, то число N(e) зростатиме. Якби довжина берегової лінії Великобританії мала певну довжину L, те число кроків циркуля з розчином (або число квадратних осередків N(e), що покривають берегову лінію на карті) було б обернено пропорціонально, а величина Ln(e)=N(e) ? e при зменшенні до прагнула б до постійної L. На жаль, розрахунки, проведені багатьма ученими, показали, що це не зовсім так. При зменшенні кроку зміряна довжина зростає. Виявилось, що взаємозв'язок зміряної довжини L(e) і кроку e може бути описана наближеним співвідношенням

Коефіцієнт D називається фрактальною розмірністю. Слово фрактал походить від латинського слова fractal - дріб, нецілий. Множина називається фрактальною, якщо воно має нецілу розмірність. Для Норвегії D=1,52, а для Великобританії D=1,3. Таким чином, берегова лінія Норвегії і Великобританії - фрактал з фрактальною розмірністю D. Розрахунки були також проведені і для кола, і фрактальна розмірність кола D=1, що і слід було чекати. Таким чином, фрактальна розмірність - узагальнення звичайної розмірності.

Як це розуміти і що б це могло означати? Математики почали згадувати, чи було що-небудь подібне раніше в математиці чи ні? І пригадали! Розглянемо частину деякої лінії АВ на площині (Рис. 3). Візьмемо квадрат з ребром e і запитаємо себе: скільки потрібно квадратиків N(е) з ребром довжиною е, щоб покрити лінію АВ такими квадратиками? Видно, що N(e) пропорційно

Аналогічно, якщо замкнуту обмежену область на площині (Рис. 4) покрити квадратною сіткою із стороною e, то мінімальне число квадратиків із стороною е, що покривають область, буде рівне

Якщо ми розглянемо замкнуту обмежену область в тривимірному просторі і візьмемо кубик з ребром e, то кількість кубиків, що заповнюють цю область

Визначимо фрактальну розмірність виходячи з вище за викладене в загальному випадку таким чином:

Візьмемо логарифм від лівої і правої частин

Переходячи до межі при e, прагнучому до нуля (N, прагнучому до нескінченності), отримаємо

Ця рівність є визначенням розмірності яка позначається d.

Повернемося до наший початковому завданню. Розглянемо довжину берегової лінії L(е)= аoe1-d і зробимо наступні перетворення:

тобто N(e) пропорційно

і переходячи до межі, маємо

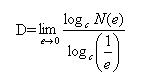
Таким чином, d - розмірність.

Розрахунки показують, що

Таким чином, берегові лінії Великобританії і Норвегії є фракталами і мають фрактальну розмірність 1,3 і 1,52, відповідно.