Розв’язання задачі без урахування власної ваги

Брус, який розглядається (рис. 1.1,а), є статично визначеним і має три ділянки, номери яких позначені римськими цифрами. При визначенні і розрахунок ведемо від вільного кінця (у цьому разі реакцію в закріпленні бруса аналітично визначати не потрібно), тобто визначаємо та по силах, розташованих вище розглядуваних поперечних перерізів (рис. 1.2,а,б,в).

М_В 1:200 (указати обраний Вами вертикальний масштаб)

На епюрі N 1 см  100 кН, а на епюрі  1 см  0,2 МПа

(указати обрані Вами співвідношення)

Рис. 1.1

а) ділянка І б) ділянка ІІ в) ділянка ІІІ

Рис. 1.2

Ділянка І (0 4 м):

,

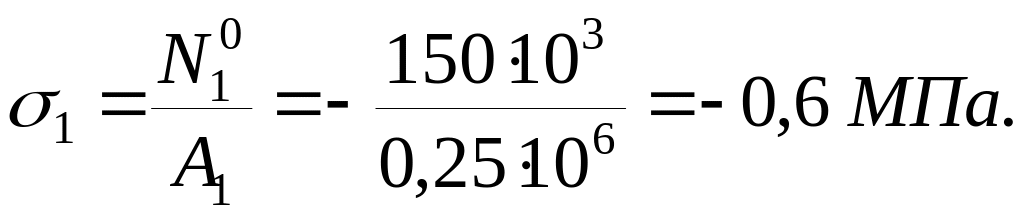
Ділянка II ( ):

,

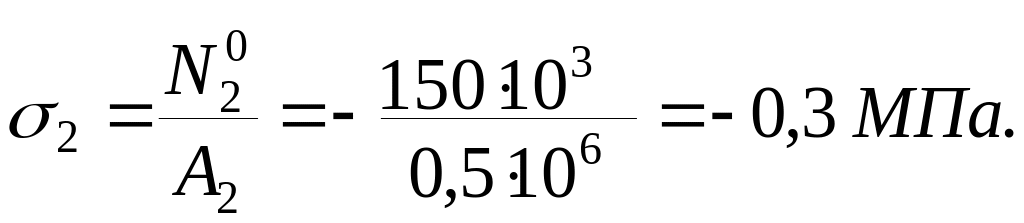
Ділянка ІІІ ( )

,

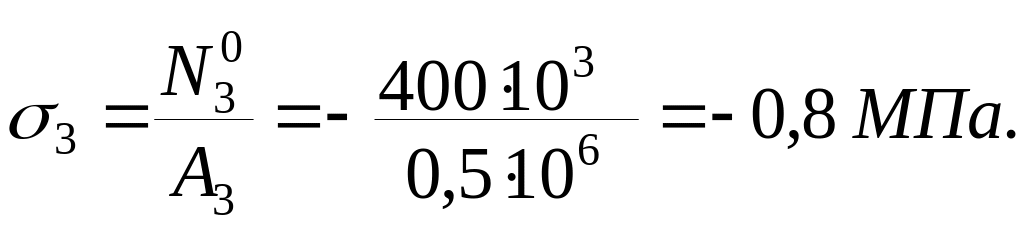
За отриманими даними будуємо епюри і (рис. 1.1,б,в).

Небезпечними будуть усі поперечні перерізи третьої ділянки. Умова міцності для цих перерізів виконується:

.

Таким чином міцність усього бруса забезпечена.

Повна деформація бруса дорівнює алгебраїчній сумі абсолютних деформацій усіх ділянок:

,

де – абсолютні деформації ділянок бруса.

Визначаємо абсолютні деформації ділянок:

.

Повна деформація бруса буде такою

.

Переміщення перерізу I-I відносно жорсткого закріплення ( ) дорівнює алгебраїчній сумі абсолютних деформацій усіх частин бруса, розташованих між перерізом і закріпленням. У нашому випадку між перерізом і закріпленням розташована тільки частина третьої ділянки довжини 4 м і переміщення перерізу буде таким

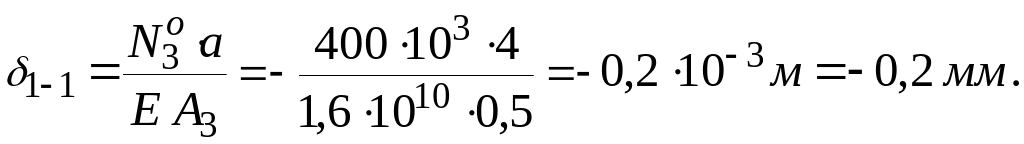
Визначимо розміри квадратного поперечного перерізу кожної ділянки бруса, які забезпечать найменші витрати матеріалу.

Запишемо умову міцності для i-ї ділянки

.

Потрібна площа поперечного перерізу i-ї ділянки буде

,

а відповідні розміри квадратного поперечного перерізу ділянки визначаться за формулою

.

Для ділянки І:

,

.

Для ділянки ІІ:

,

.

Для ділянки ІІІ:

,

.

Розв’язання задачі з урахуванням власної ваги

Згідно з рис. 1.3,а та рис. 1.4,а,б,в визначаємо і на кожній з трьох ділянок.

Ділянка І ( ):

, , ,

.

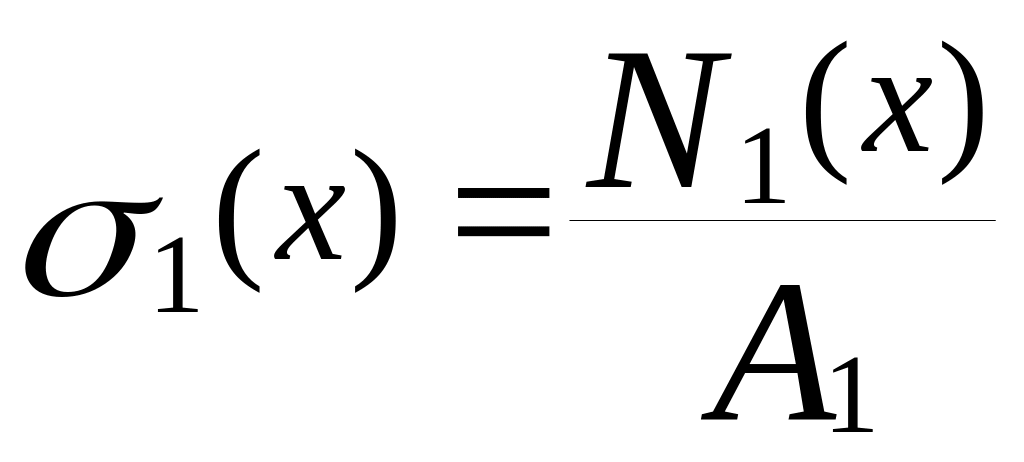При x = 0: ,

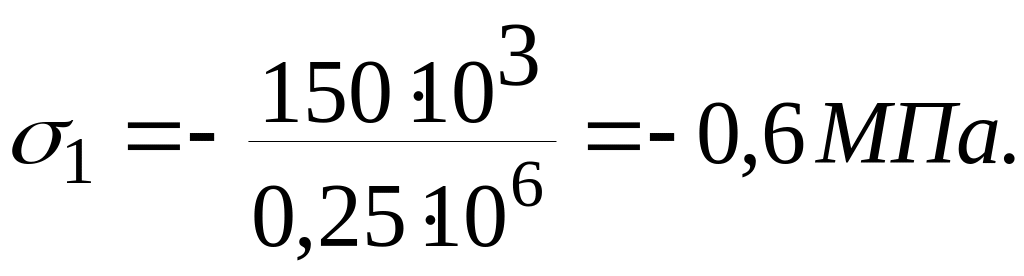
При x = 4 м:

(другий член у виразі для N₁ – це власна вага ділянки І Q₁=18 кH),

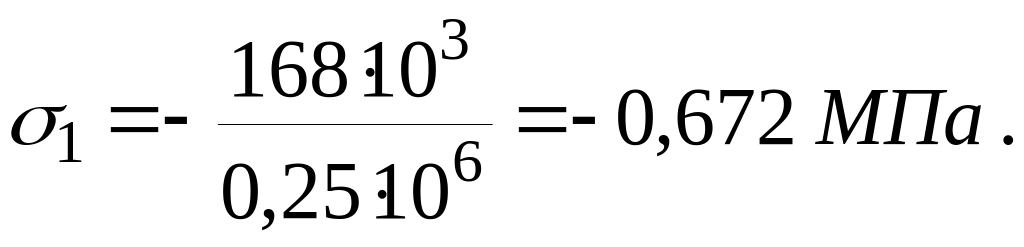
М_В 1:200 (указати обраний Вами вертикальний масштаб)

На епюрі N 1 см  120 кН, а на епюрі  1 см  0,25 МПа (указати обрані Вами співвідношення)

Рис. 1.3

а) ділянка І б) ділянка ІІ в) ділянка ІІІ

Рис. 1.4

Ділянка ІІ ( ):

, ,

, .

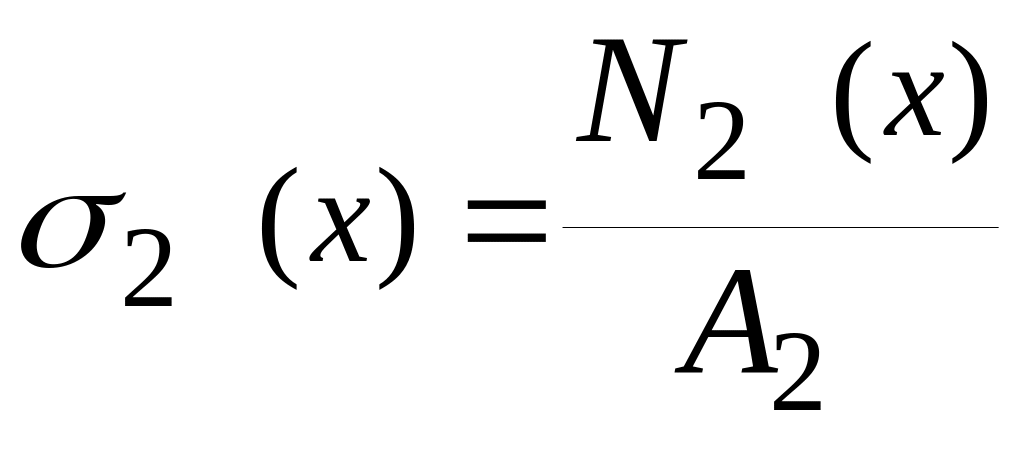При x = 4 м: ,

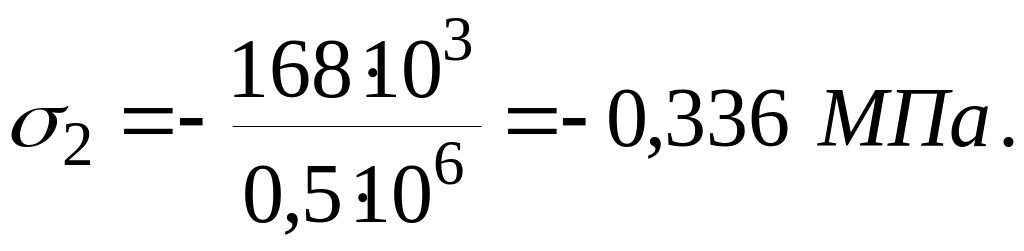
При x = 6 м:

(третій член у виразі для N₂ – це власна вага ділянки ІІ Q₂=18 кH),

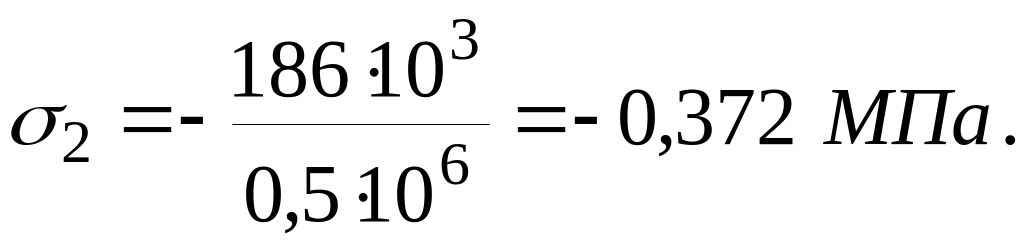
Ділянка ІІІ ( ):

, ,

, .

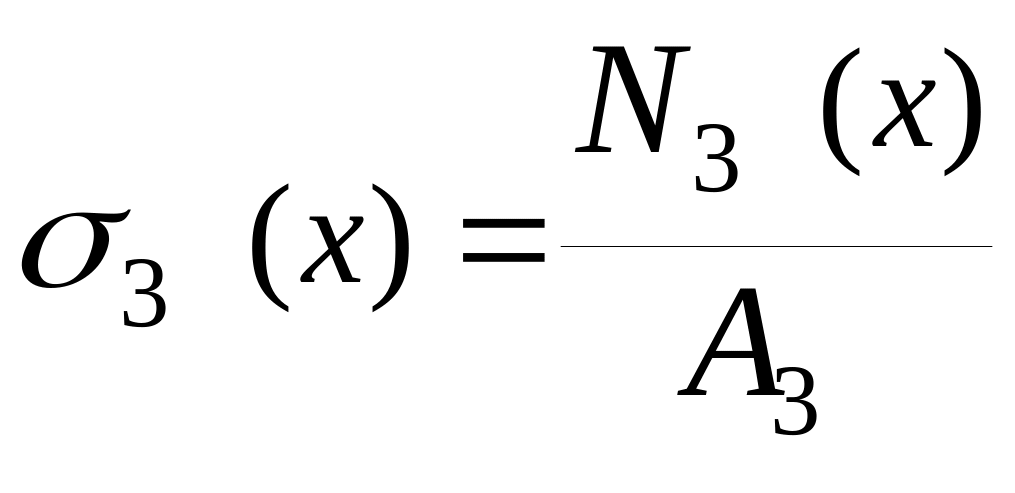При х = 6 м; ,

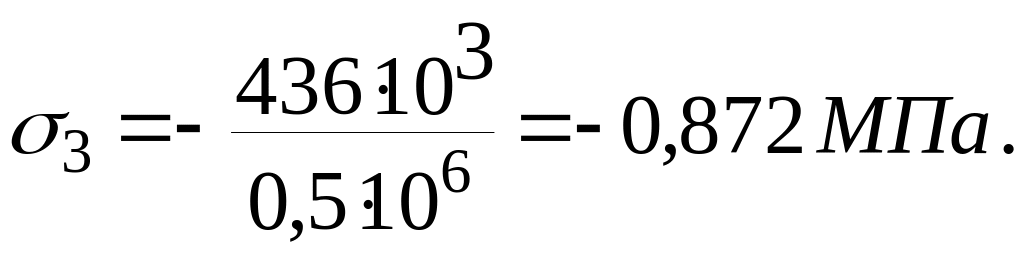
При x=11 м:

(п’ятий член у виразі для N₃ – це власна вага ділянки ІІІ Q₃=45 кH),

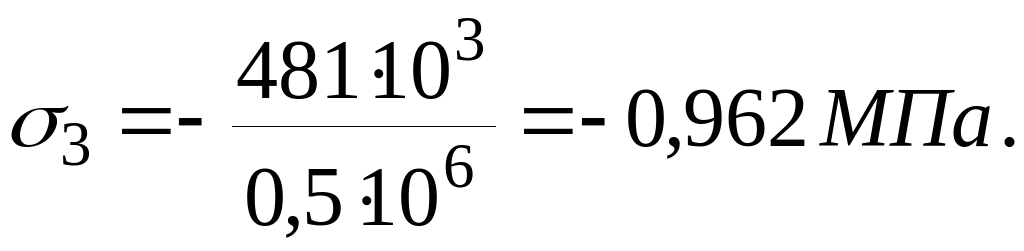
За отриманими даними будуємо епюри і (рис. 1.3,б,в).

Небезпечним буде нижній поперечний переріз бруса, де виникає . Умова міцності для цього перерізу виконується:

.

Таким чином міцність усього бруса з урахуванням власної ваги теж забезпечена. (Без урахування власної ваги .)

Повна деформація бруса дорівнює алгебраїчній сумі абсолютних деформацій усіх ділянок:

,

де – абсолютні деформації ділянок бруса.

Визначаємо абсолютні деформації ділянок:

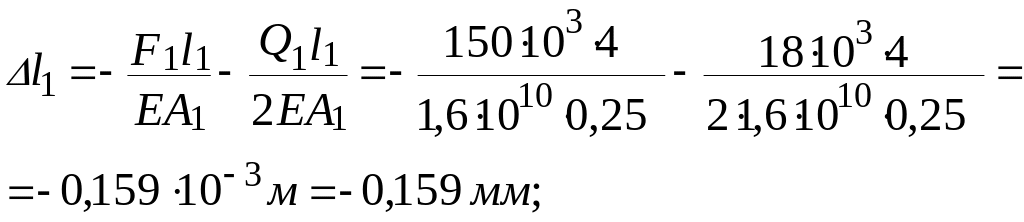
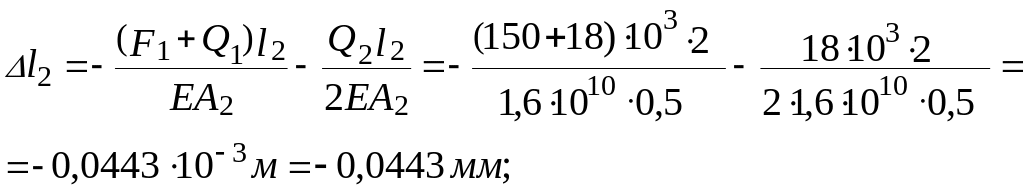
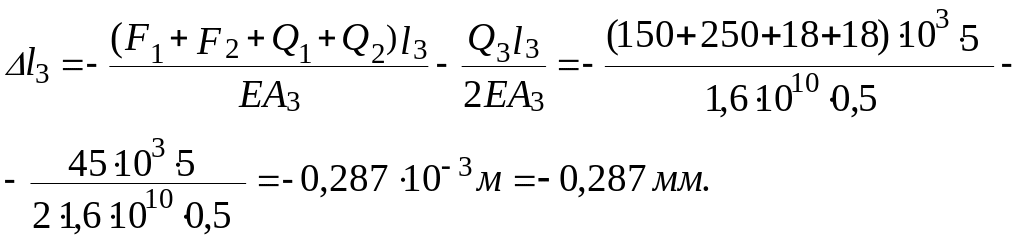
Тоді повна деформація бруса з урахуванням власної ваги буде такою:

Без урахування власної ваги .

Переміщення перерізу I-I відносно жорсткого закріплення ( ) дорівнює алгебраїчній сумі абсолютних деформацій усіх частин бруса, розташованих між перерізом і закріпленням. У нашому випадку між перерізом і закріпленням розташована тільки частина третьої ділянки довжини 4 м і переміщення перерізу таке

,

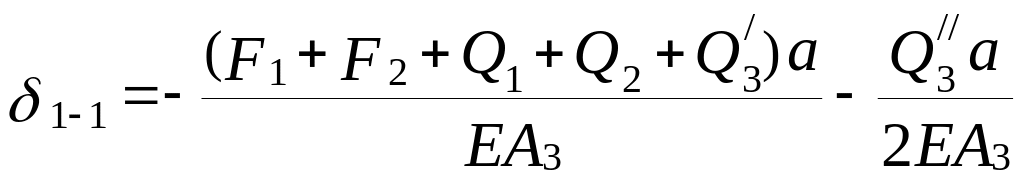де - власна вага верхньої частини ділянки І, а - власна вага нижньої частини цієї ж ділянки. Частини відсікаються перерізом I-I.

Підставимо числові значення величин

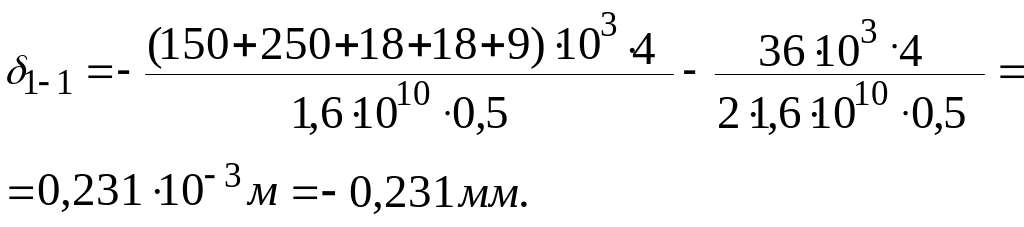
Без урахування власної ваги

Визначимо розміри квадратного поперечного перерізу кожної ділянки бруса, які забезпечать найменші витрати матеріалу.

З епюри видно, що небезпечні перерізи за нормальними напруженнями розташовані в кінці кожної ділянки. Для цих перерізів запишемо відповідні умови міцності, потім визначимо потрібні площі поперечних перерізів і відповідні їх розміри .

Для ділянки І: , звідки

.

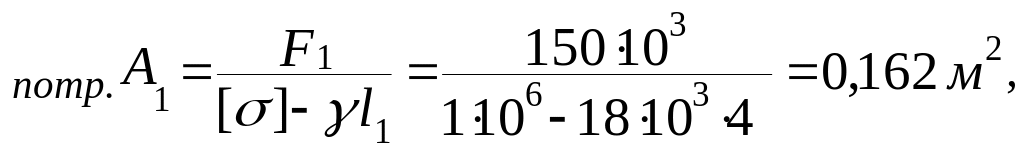
Для ділянки ІІ: ,

де - нова вага ділянки І,

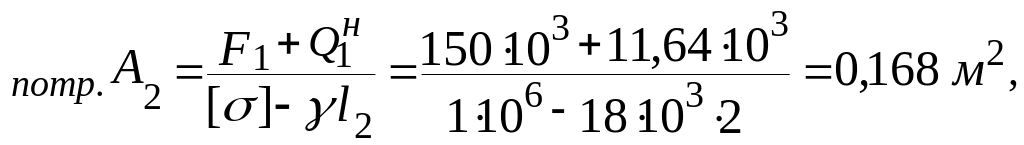
Для ділянки Ш: ,

де - нова вага ділянки ІІ,

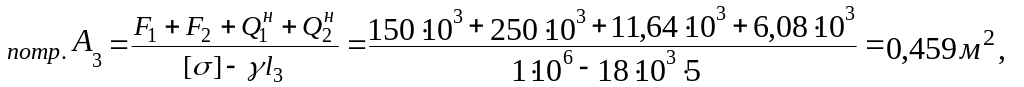
Без урахування власної ваги , , .

Порівнявши відповідні величини, бачимо, що в розглянутому випадку урахування власної ваги необхідне.

Приклад розв’язання задачі № 2. Горизонтальний абсолютно жорсткий брус АВ підтримується стальними стержнями 1 і 2 (рис.1.5,а), кінці яких шарнірно закріплені. При а =1 м, b =4 м, с =2 м, d =3 м, A₁=4 см²=4·10^-4 м², А₂ =6 см²=6·10^-4 м², Е =2·10⁵ МПа, α=45^о і [σ]=160 МПа, потрібно визначити наступне: а) зусилля та напруження в стержнях (в частинах сили ); б) допустиме навантаження .

Скористаємось методом перерізів: розріжемо перший та другий стержні та залишимо верхню частину системи (рис. 1.5,б), зобразивши додатними невідомі поздовжні зусилля , (спрямувавши їх в бік відкинутої частини). Враховуємо, що в шарнірно-нерухомій опорі С присутні дві складові опорної реакції: і . Для визначення чотирьох невідомих ( , , і ) можна скласти лише три незалежні рівняння статики. Таким чином ССН=4-3=1 і система є один раз статично невизначеною. Для однозначного розв’язання задачі треба скласти одне додаткове рівняння – рівняння сумісності деформацій.

В задачі необхідно визначити тільки поздовжні зусилля і , тому з можливих трьох рівнянь статики залишаємо тільки одне: (до цього рівняння не увійдуть невідомі складові опорної реакції і ):

. (І)

а) б)

в)

Рис. 1.5

Щоб скласти додаткове рівняння, розглянемо деформацію заданої системи. Побудуємо план переміщень (рис. 1.5,а): під дією зосередженої сили абсолютно жорсткий брус, не викривляючись, повернеться навколо опорного шарніру С і точка А зміститься вниз; перший стержень укоротиться (стиснеться) на величину поздовжньої деформації , яку ми й відкладаємо вздовж початкового положення першого стержня (рис. 1.5,а,в); потім проводимо два перпендикуляри: один до жорсткого бруса через шарнір D, а другий до укороченого першого стержня (переміщення за дугами окружностей апроксимуємо переміщеннями за перпендикулярами, це можна робити з-за молості деформацій); там де вказані перпендикуляри перетинаються й буде нове положення вузла D'; орієнтуючись на вузли С і D', зображуємо нове положення бруса та першого стержня (штрихові лінії); вузол В, як належав нижній грані бруса до деформації системи, так і повинен їй належати й після деформації (вузол В'), тобто другий стержень подовжується на величину .

З подібності трикутників та маємо

. (ІІ)

Зважаючи на те, що і (рис. 1.5,а,в),

вираз (II) набуває такий вигляд:

. (ІІІ)

Це й є додаткове рівняння – рівняння сумісності деформацій стержнів 1 і 2.

У рівняннях статики, які складаються в методі перерізів, усі невідомі зусилля вважаються додатними й такими ж вони зображуються (розтягуючими на рис. 1.5,б). Проте, на деформованій схемі деякі стержні можуть бути стиснутими (стержень 1 на рис. 1.5,а). У цьому випадку, для приведення у відповідність знаків зусиль та деформацій, вирази для деформацій стиснутих стержнів треба записати зі знаком “–“.

Для даної задачі ,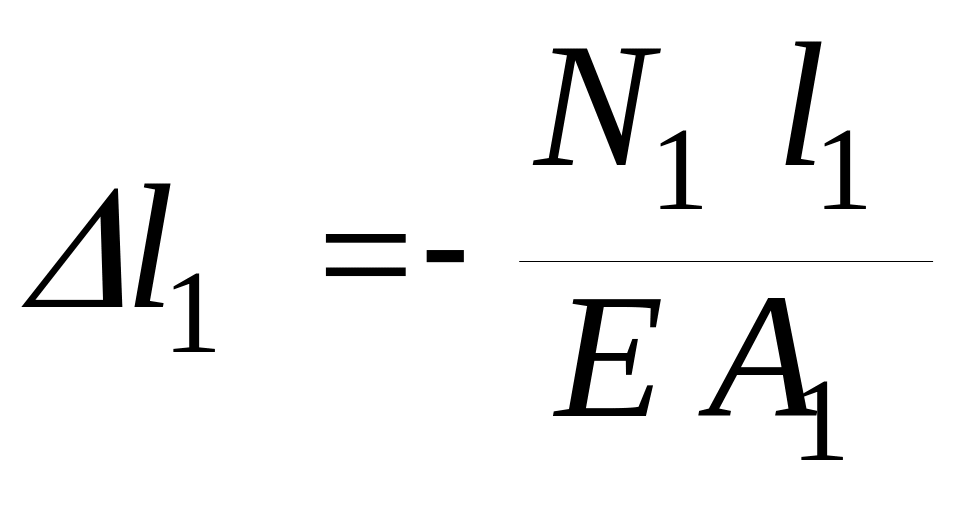

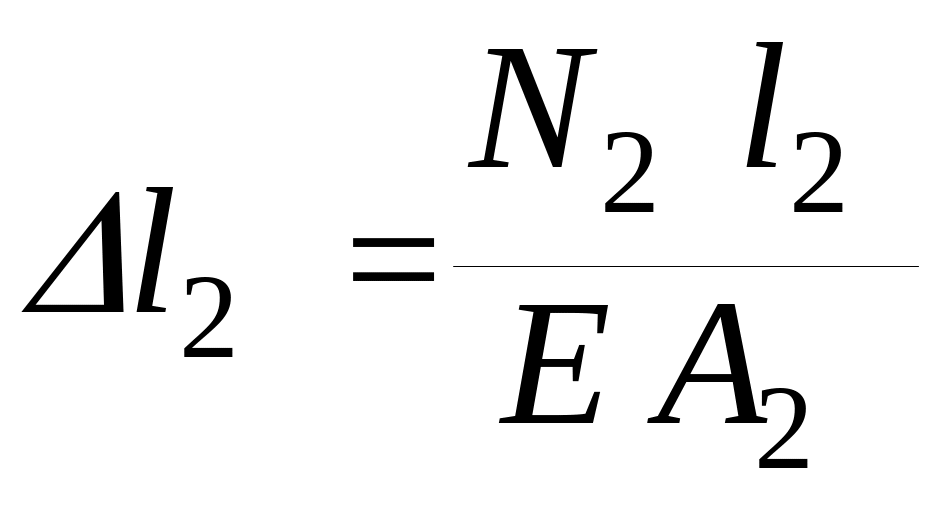
і рівняння сумісності деформацій (ІІІ) остаточно запишеться так:

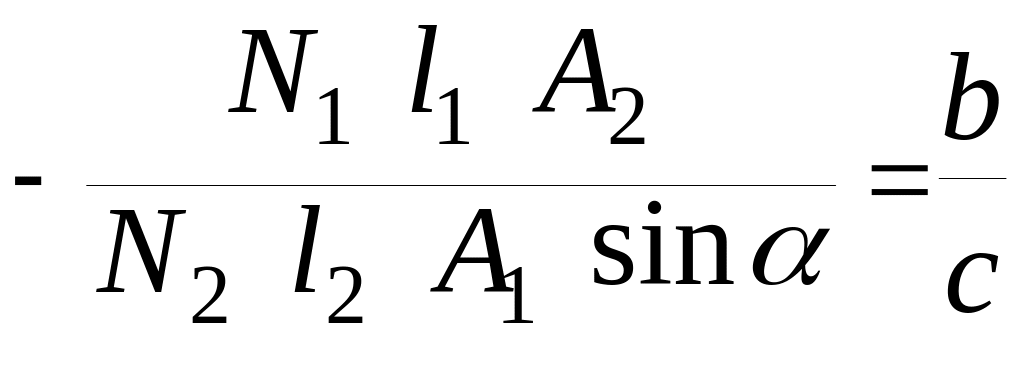. (ІV)

Визначимо довжини стержнів

, = d =3 м.

Підставивши в рівняння (I, IV) числові значення a, b, c, , , , та , отримуємо наступну систему рівнянь

,

.

Після розв’язання системи маємо

, .

Визначаємо нормальні напруження в стержнях

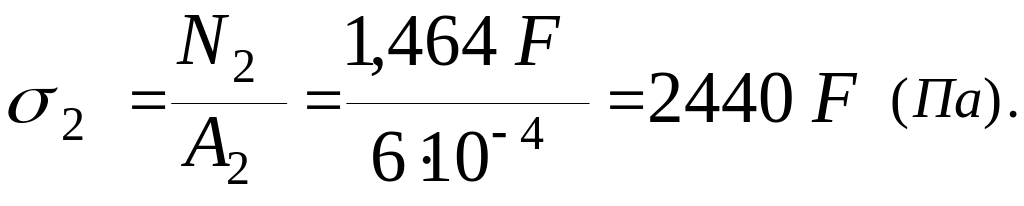
Як бачимо, найбільш напруженим (небезпечним) буде стержень 2 (в ньому виникає найбільше за абсолютним значенням нормальне напруження). Запишемо для нього умову міцності за нормальними напруженнями

,

з якої одержуємо допустиму величину зосередженої сили