5. Приклад.

Побудувати математичну модель і знайти оптимальний розв’язок задачі, яка є двоїстою до задачі лінійного програмування для якої задана математична модель і її оптимальний розв’язок:

Оптимальний розв’язок:

Розв’язування:

1. Побудуємо математичну модель двоїстої задачі. Для цього математичну модель заданої задачі зведемо до стандартного виду. Так як , всі обмеження повинні мати знак “ ”. Цій умові не задовольняє перше і третє обмеження даної задачі, тому помножимо їх на (-1). Математична модель запишеться у вигляді:

або:

• Так як пряма задача має три обмеження, то в двоїстій задачі буде три змінні:

• Цільова функція 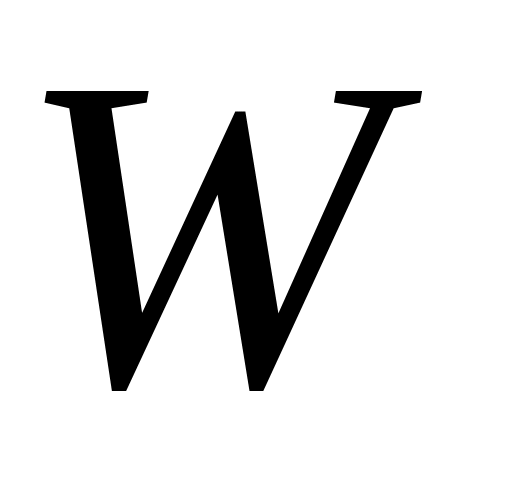має коефіцієнти: 6; 9; 3 (вільні члени обмежень прямої задачі) і прямує до мінімуму (так як цільова функція прямої задачі прямує до максимуму), а тому набуває вигляду:

.

• Матриця коефіцієнтів прямої задачі:

• Матриця коефіцієнтів двоїстої задачі – транспонована матриці :

• Обмеження двоїстої задачі:

Таким чином, математична модель двоїстої задачі:

2. Знайдемо оптимальні розв’язки двоїстої задачі, не розв’язуючи її.

• Підставимо в обмеження прямої задачі оптимальні значення і

, тому ;

, тому ;

, тому .

• Так як 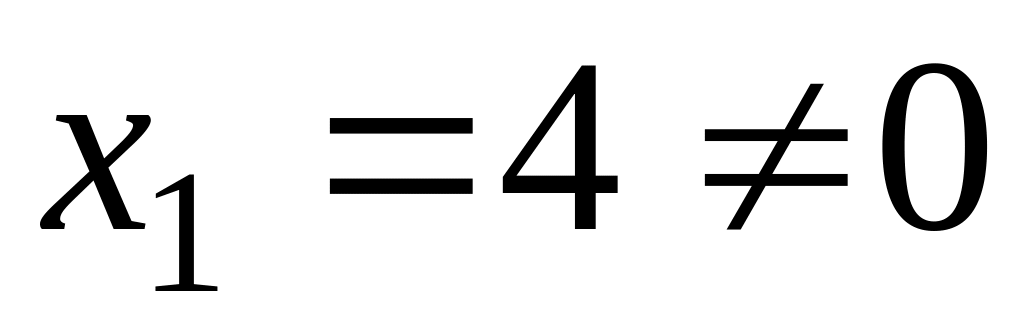, тому перше обмеження двоїстої задачі – рівняння, якщо підставити оптимальні значення змінних і , тобто:

.

• Так як 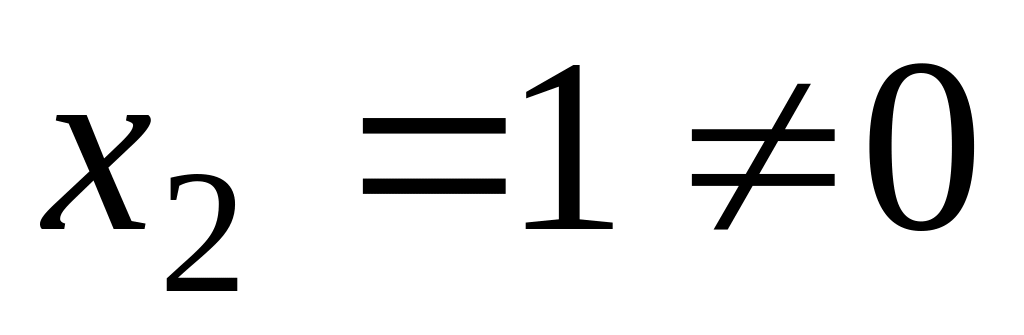, тому і друге обмеження – рівняння:

.

• Розв’яжeмо систему отриманих рівнянь, враховуючи, що :

Таким чином, оптимальний розв’язок двоїстої задачі:

3. Розглянемо випадок розв’язування двоїстої задачі, якщо відома остання симплекс – таблиця прямої задачі:

			2	1	0	0	0
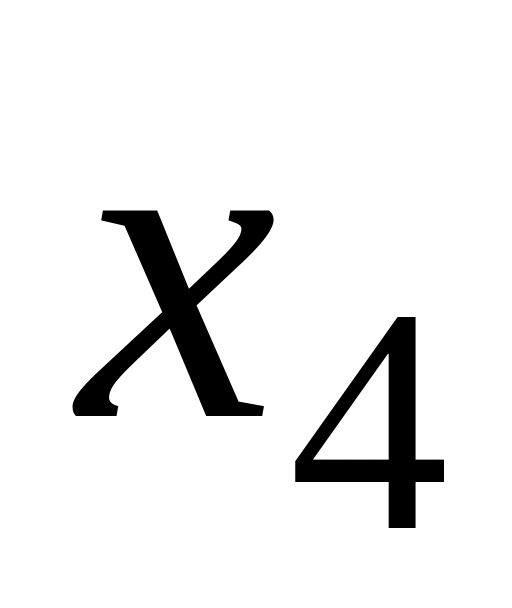
0		7	0	0	1	-2/3	7/3
1		1	0	1	0	1/3	-2/3
2		4	1	0	0	1/3	1/3
			0	0	0	1	0

Відповідь:

Завдання для самостійного розв’язування

Задана математична модель прямої задачі. Знайти її оптимальні розв’язки за допомогою ЕОМ в ОЦ інституту. Побудувати математичну модель двоїстої задачі, а також за допомогою теорем двоїстості знайти її оптимальні розв’язки (2 способами)

Варіант 1.

Варіант 3.

Варіант 5.

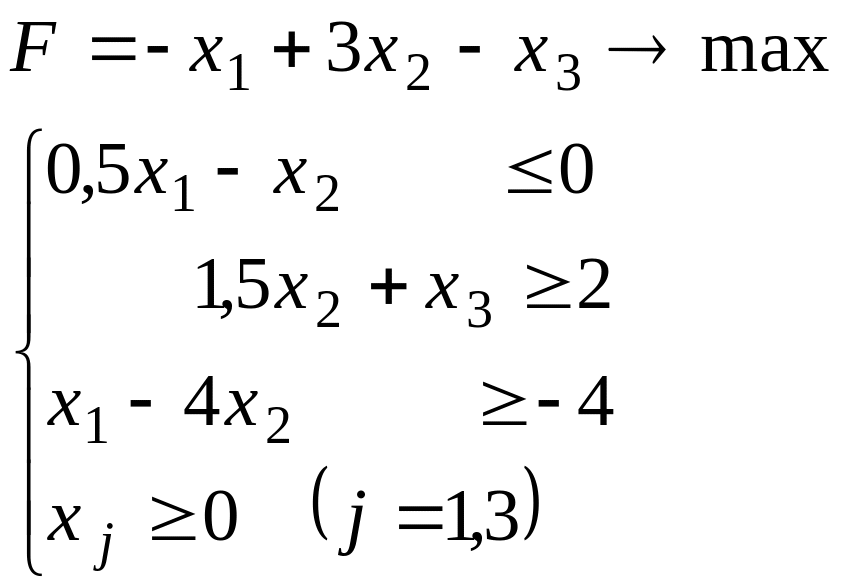
Варіант 2.

Варіант 4.

Варіант 6.

Варіант 7.

Варіант 9.

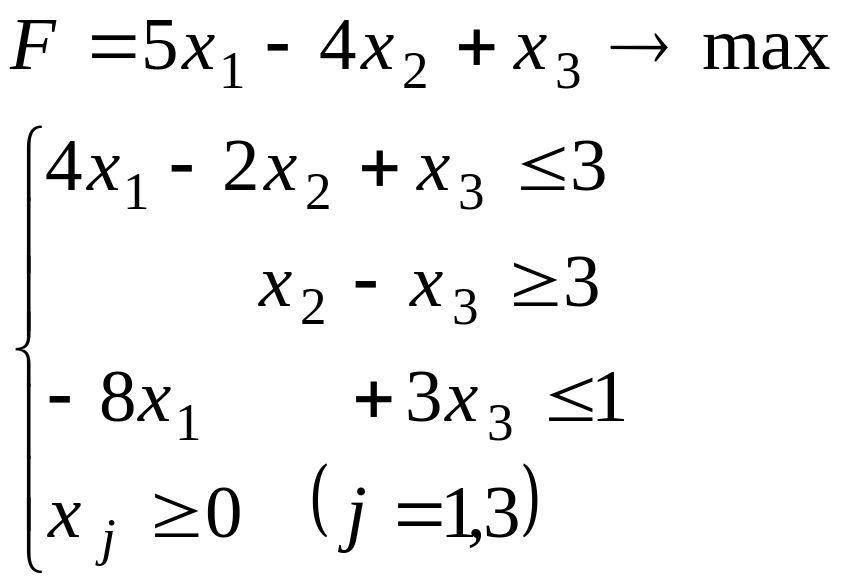
Варіант 11.

Варіант 13.

Варіант 8.

Варіант 10.

Варіант 12.

Варіант 14.

Варіант 15.

Варіант 17.

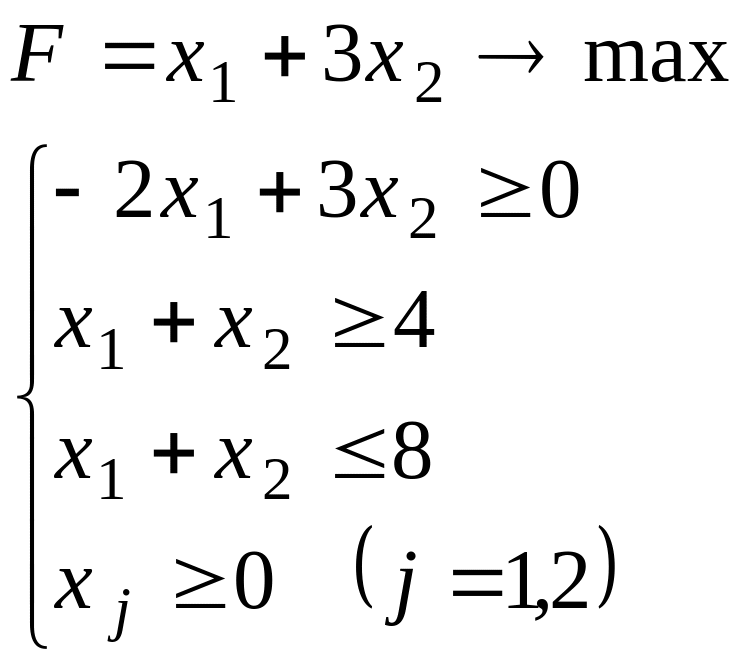
Варіант 19.

Варіант 21.

Варіант 16.

Варіант 18.

Варіант 20.

Варіант 22.

Варіант 23.

Варіант 25.

Варіант 27.

Варіант 29.

Варіант 24.

Варіант 26.

Варіант 28.

Варіант 30.