10

Введение

При проведении большинства технологических процессов пищевых производств возникает необходимость в транспортировке рабочих сред, которая осуществляется с помощью насосов (жидкие среды) либо вентиляторов и компрессоров (газообразные среды). Выбор гидравлических машин производится по двум параметрам: объемному расходу рабочей среды и требуемому напору (либо давлению, развиваемому на выходе из гидромашины ). При совместной работе трубопровода (воздуховода) и гидравлической машины давление расходуется на преодоление гидравлического сопротивления. В общем случае оно складывается из потерь на: преодоление сил трения по длине трубопровода , преодоление местных сопротивлений , создание гидродинамического давления , подъем жидкости (газа) и дополнительных потерь .

(1)

Потери давления на преодоление трения по длине трубопровода – это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают пропорционально длине трубы при постоянном расходе среды. Эти потери обусловлены не только трением среды о стенки трубопроводов, аппаратов, но и трением между слоями жидкости. Поэтому эти потери имеют место не только в шероховатых, но и в гладких трубах и отсутствуют при транспортировке идеальных жидкостей. Для расчёта используется формула Дарси-Вейсбаха

, (2)

где - коэффициент гидравлического трения;

- длина трубопровода, м;

- плотность среды, кг/м³;

- средняя скорость движения среды, м/с;

- эквивалентный диаметр трубопровода, м.

Эквивалентный диаметр трубопровода (канала) определяется по зависимости

, (3)

где - площадь живого сечения потока, м²;

- смоченный периметр трубопровода (канала), м.

Площадь живого сечения кожухотрубного теплообменника определяется по формуле

, (4)

где - число труб теплообменника, шт.;

- внутренний диаметр одной трубки, м.

Коэффициент трения , входящий в уравнение (2), зависит в основном от режима движения среды по трубопроводу и определяется с помощью соответствующих графиков [2, 3] и эмпирических уравнений, которые имеют вид

при Re<2.3 10³ (5)

при 4 10³<Re<10⁵ (6)

при (7)

где - высота шероховатости стенки, м.

Режим движения определяется по значению числа Рейнольдса, который характеризуется соотношением сил инерции и сил вязкостного трения

, (8)

где - динамическая вязкость среды, Па с.

Средняя скорость, входящая в формулы (2) и (5) – это такая, одинаковая для всех точек сечения, скорость, при которой за единицу времени через данное сечение проходит тот же объём среды, что и при действительном распределении скоростей по сечению потока. Среднюю скорость определяют из уравнения расхода

, (9)

где – объёмный расход, т.е. объём среды, проходящей через живое сечение потока за единицу времени, м³/с.

Местные потери энергии обусловлены так называемыми местными сопротивлениями, т.е. участками трубопроводов или аппаратов, где происходит изменение скорости потока либо по величине, либо по направлению. К их числу относятся вход потока в трубу и выход из неё, внезапные сужения и расширения, отводы, колена, тройники, запорные и регулирующие устройства (краны, вентили, задвижки, заслонки и т.п.).

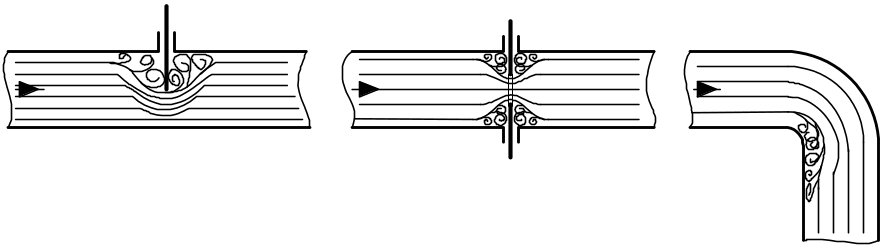
а б в

Рисунок 1- Виды местных гидравлических сопротивлений:

а) – заслонка; б) – диафрагма; в) – колено.

Возникновение потерь энергии на преодоление местных сопротивлений объясняется тем, что при протекании через них среды изменяется скорость её движения, и возникают вихри, на образование которых затрачивается дополнительная энергия потока. Вихри образуются за местом отрыва потока от стенок либо в пространстве со значительной неоднородностью полей давления и представляют собой области, в которых частицы среды движутся, в основном, по замкнутым кривым или близким к ним траекториям. На рисунке 1 показаны некоторые виды местных сопротивлений, отрыв потока от стенок и вихреобразования.

Величина местных потерь зависит как от скорости движения среды, так и от вида местного сопротивления. Последний фактор учитывается коэффициентом местного сопротивления . Значение рассчитывается по уравнению

, (10)

где – количество местных сопротивлений.

Величина гидродинамического давления зависит от плотности транспортирующей среды и скорости ее перемещения и представляет собой разность давлений, затрачиваемую на придание потоку кинетической энергии движения (значение скорости здесь берется на выходе потока из гидравлической сети):

(11)

В реальной инженерной практике значительно меньше остальных составляющих, однако для простых и коротких трубопроводов оно соизмеримо с ними.

Потери давления на подъем представляют собой затраты энергии на подъем потока плотностью на высоту :

. (12)

Дополнительные потери определяются затратами энергии на преодоление возможной разности давлений в пространстве нагнетания ( ) и всасывания ( ):

. (13)

В тех случаях, когда расчет трубопроводов затруднен (либо вовсе невозможен) при сложной форме каналов, неизвестных характеристиках среды, величина потерь давления может быть определена из критериального уравнения, полученного на основе теории размерностей. Известно, что общее гидравлическое сопротивление трубопровода (аппарата) зависит от скорости движения среды , ее плотности , динамической вязкости , а также от длины трубы . Для горизонтально расположенных аппаратов и трубопроводов можно пренебречь действием силы тяжести. Тогда функциональная зависимость от влияющих на него факторов примет вид

(14)

Связь между величинами, входящими в уравнение (14), можно представить в виде степенного уравнения:

, (15)

где - показатели степени, указывающие на силу влияния соответствующего параметра на общее гидравлическое сопротивление.

В системе СИ в качестве основных единиц измерения используются кг, м и с. Выразив размерности входящих в уравнение (15) величин через эти единицы, получим

(16)

Раскрываем скобки и группируем члены с одинаковыми основаниями

(17)

Из условия размерной однородности левой и правой частей уравнения (17) показатели степеней при одинаковых основных единицах измерения в обеих частях этого уравнения должны быть равны, т.е.

(18)

Полученная система из трех уравнений является незамкнутой, т.к. содержит четыре неизвестные величины. Поэтому одну из неизвестных величин принимаем за известную (например, d) и три остальных (a, c, b) выражаем через нее. В результате получим

(19)