Функція передачі неідеального 3-розрядного цап

Мал.2.12

ФУНКЦІЯ ПЕРЕДАЧІ НЕІДЕАЛЬНОГО 3-РОЗРЯДНОГО ЦАП

Мал.2.13

Визначення відсутніх кодів складніше, ніж визначення немонотонності. Всі АЦП характеризуються деяким шумом переходу (transition noise), що ілюструється на рис.2.14 (уявіть собі цей шум як мигтіння останньої цифри цифрового вольтметра між сусідніми значеннями). У міру зростання роздільної здатності діапазон вхідного сигналу, відповідний рівню шуму переходу, може досягти або навіть перевищити значення сигналу, відповідне одиниці молодшого розряду. У такому разі, особливо у поєднанні з негативною DNL- погрішністю, може трапитися так, що з'являться деякі (або навіть все) коди, де шум переходу буде присутній у всьому діапазоні значень вхідних сигналів. Таким чином, можливе існування деяких кодів, для яких не існує значення вхідного сигналу, при якому цей код гарантовано б з'явився на виході, хоч і може існувати деякий діапазон вхідного сигналу, при якому іноді з'являтиметься цей код.

Сумісна дія шуму переходу коду ацп і диференціальній нелінійності (dnl)

Мал.2.14

Для АЦП з невисокою роздільною здатністю можна визначити умову відсутності пропущених кодів як поєднання шуму переходу і диференціальної нелінійності, при якому гарантувався б деякий рівень (скажімо, 0.2 LSB) вільного від шуму коду для всіх кодів. Проте при цьому неможливо досягти такої високої роздільної здатності, яку забезпечують сучасні сигма-дельта АЦП, або навіть меншій роздільній здатності для АЦП з широкою смугою пропускання. У цих випадках виробник повинен визначати рівні шумів і роздільну здатність яким-небудь іншим способом. Не так важливо, який метод використовується, але специфікація повинна містити чітке визначення використовуваного методу і очікувані характеристики.

Шум квантування ідеального n-розрядного ацп

Мал.2.5

Теорема Котельникова-Шеннона

Введення.

Нагадаємо визначення понять дискретизації і інтерполяції.

Визначення. Представлення безперервного (аналогового) сигналу x(t) дискретною

послідовністю відліків x(t_k)=x(k∆t ), по яких із заданою точністю можна

відновити початковий безперервний сигнал, називається дискретизацією на рівномірній

сітці.

Визначення. Процес відновлення дискретизованого сигналу називається

інтерполяцією.

Допустимо, у нас є безперервне зображення i(x,y). Після дискретизації ми отримуємо

дискретне зображення I(x_k,y_m). Потім інтерполюємо його і переходимо до зображення

i’(x,y).

Природно виникає питання :

Як потрібно проводити дискретизацію, щоб не відбувалася втрата інформації

тобто за яких умов початкове зображення i(x,y) співпадає з відновленим

i’(x,y)?

Відповідь на це питання може бути отримана з теореми Котельникова-Шеннона.

Теорема Котельникова-Шеннона.

Нагадаємо визначення просторів L₁ і L₂ і норм в них.

Визначення. Простором L₁(R) називається простір комплекснозначних або

дійсних функцій, інтегрованих на безлічі R.

Визначення. Нормою елементу f в просторі L₁(R) називається величина

Визначення. Простором L₂(R) називається простір комплекснозначних або

дійсних функцій інтегрованих на безлічі R з квадратом.

L₂(R) – евклідовий простір, скалярний твір для елементів f і g в нім вводиться

як

Визначення. Нормою елементу f в просторі L₂(R) називається величина

Перетворення Фурє F( γ) функції f(t) визначається як

для всіх γR.

Позначимо через A(R) безліч перетворень Фурє всіх функцій f, що належать

простору L₁(R).

Теорема. Нехай fL₁(R) ∩ A(R) або f  L₂ (R). Припустимо, дані константи T, Ω >0

такі що

F(γ) рівна 0 поза сегментом [-Ω, Ω] (1)

та

0<2T≤1. (2)

Тоді

(3)

причому ряд сходиться по точечно на R, якщо f L₁ (R)∩А(R), і ряд сходиться

рівномірно, якщо f L₂ (R) (сигнал, що описується безперервною функцією часу f(t) з

обмеженим спектром, повністю визначається своїми значеннями

відліченими через інтервали часу T=1/(2 Ω), де Ω - ширина

спектру сигналу).

Доведення:

1) Нехай fL₁(R) ∩ A(R).

Всім функціям G(γ)

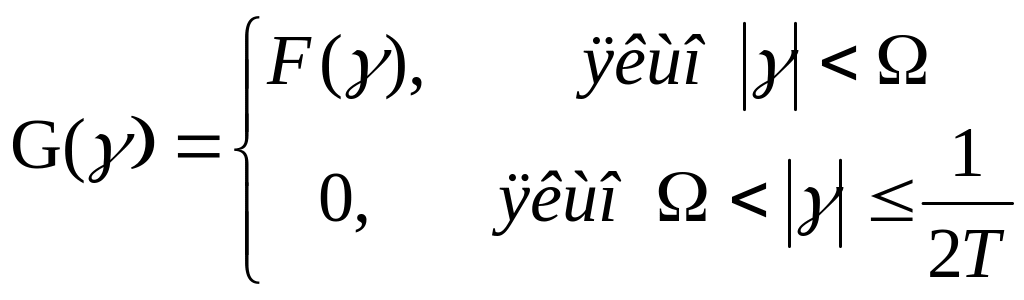
Продовжимо її періодично з періодом 1/T на R. Тоді можемо розкласти G(γ) в ряд

Фурє, що має вигляд

,

де

.

З визначення функції G(γ) та з формули звернення значить, що c_n=Tf(nT).

- <по формулі звернення>

- <по визначенню функції G(γ)>

- <підставили вираз для ряду Фурє функції G(γ)>

- < ряди Фурє інтегрованих функцій можна інтегрувати почленно>

- < отримуємо звичайним інтегруванням>

- <так як c_n=Tf(nT), помножили та поділили на 2Ω>,

2) Нехай f L₂(R).

У просторі L₂ теорема доводиться аналогічно. Так само вводимо функцію G(γ),

періодично продовжуємо її на R і розкладаємо в ряд Фурє.

Відмітимо, що за визначенням перетворення Фурє в L₂

.

Нехай S_n(γ)-n-a часткова сума Фурє функції G(γ).

Введемо функцію

Тоді,

- <по визначенню _Ω(γ)>

- <по теоремі Планшереля >

Так як S_n-n-а часткова сума ряду Фурє G, то

Використовуючи це співвідношення, (5) і (6), а також нерівність Гельдера і визначення

коефіцієнтів c_n, отримуємо потрібну в теоремі рівність.

Теорема доведена.

Зауваження до теореми Котельникова-Шеннона .

Зауваження 1. Основою доведень теореми в просторах L₁ і L₂ є можливість

переходу від перетворення Фурє до рядів Фурє.

Зауваження 2. Досліджуємо питання про те, чи можна ослабити умову (2) теореми.

Приведений нижче приклад показує, що цього зробити не можна.

Допустимо, константи T, Ω>0 задовольняють нерівності 2TΩ>1.

Візьмемо функцію

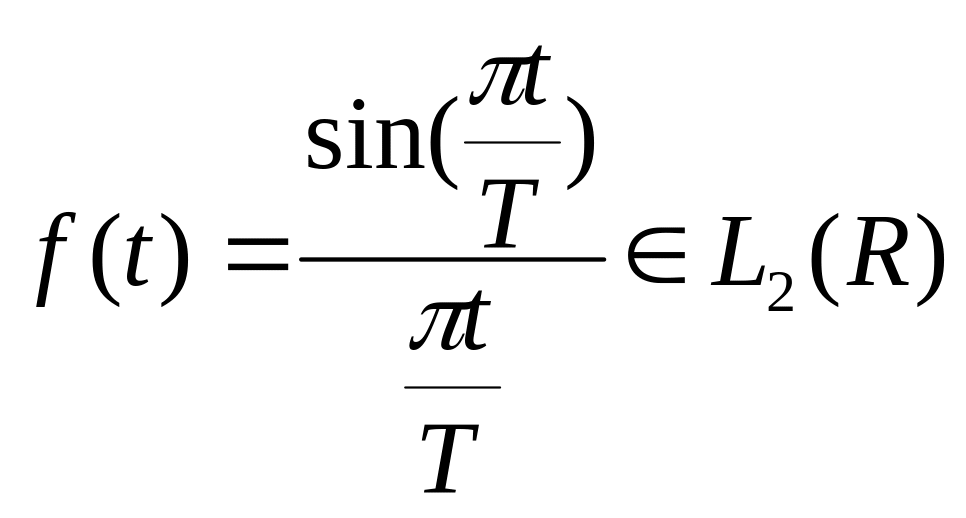
Ясно, що перетворення Фурє цій функції .

Отже, Завдання (1) виконане.

Так як , тоді права частина формули (3) .

Функції f і g не рівні, оскільки обидві безперервні на R і f(0)=1, а g(0)=2TΩ>1.

Тобто права частина не рівна лівій частині, що суперечить умові, отже

припущення про те, що 2TΩ>1 не вірно.

Отже, ми довели, що, якщо функція f розкладаємо в ряд Котельникова (3) і спектр її рівний

нулю поза відрізком [-Ω,Ω], виконується співвідношення 0<2TΩ ≤1

Зауваження 3. У формулі (3) константу T зазвичай називають періодом дискретизації

послідовність {f(nT): nZ} –послідовністю дискретизованих значень.

Частота 2Ω називається частотою Найквеста або частотою дискретизації. Це мінімальна

частота, з якою потрібно посилати імпульси, щоб не було втрати інформації.

- максимальний період дискретизації, тобто максимальний прийнятний проміжок

часу між передаваючими імпульсами.

Зауваження 4. На практиці відновлена функція f₀(t), як правило, не співпадає точно

передаваною функцією f(t). Помилка обумовлена, наприклад, тим, що спектр передаваної

функції f(t) зазвичай обмежений не різко. Це витікає хоч би з того факту, що все

реальні сигнали обмежені в часі і, отже, мають необмежені строго

спектри. Вибір інтервалів відліків T>0 означає, що всі спектральні складові

спектру з частотами >Ω_max= T не передаються і не можуть бути відновлені.

Якщо 2TΩ>1, то початкова функція не може бути відновлена, виникаючий ефект

називається aliasing.