2. Ecuaţiile de bază ale schimbătoarelor de căldură

Calculul termic al schimbătoarelor de căldură de suprafaţă se bazează pe următoareledouă ecuaţii principiale

:- ecuaţia de bilanţ termic:

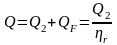
-ecuatia de transmitere a caldurii

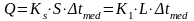in care:

;

;

În fig. 2.1 se prezintă principalele mărimi care apar în calculul termic al schimbătoarelor de căldură de suprafaţă

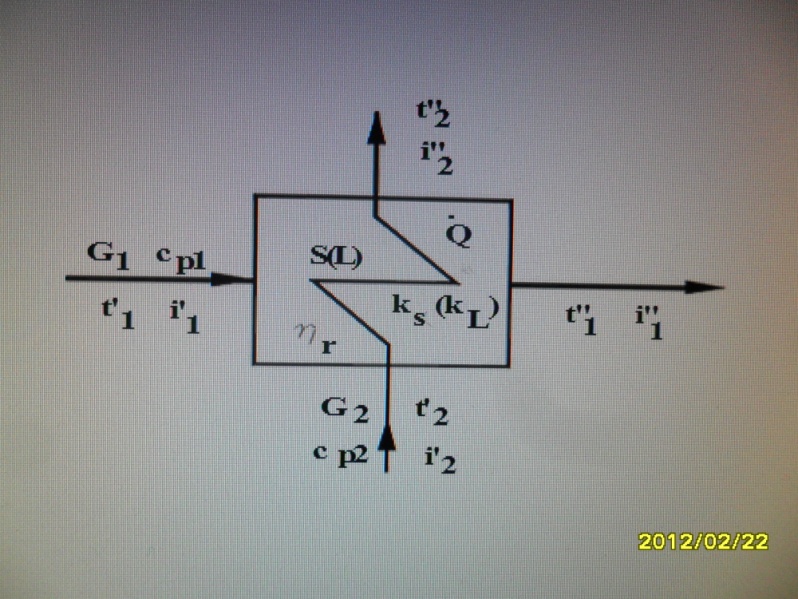
Q1 Q2-fluxul de caldura cedat de agentul cald,respective primit de agentul rece,in W

Qp-pierderele de caldura ale aparatului in mediul ambient,in W

- coef de retinere a caldurii in aparat

Q- sarcina termica a aparatului de schimb de caldura, inW. De obicei Q=Q2

S- suprafata de schimb de caldura

L- lungimea totala a tevilor

Ks K1- coef global de transfer de caldura

t med –diferenta medie de temperature a agentilor termici

t1 t2 – temp medie in aparat a agentului rece si cald

G1 G2 – debitul masic de agent. inKg/s

Cp1 Cp2-caldura specifica la presiune constanta a agentului. J/(KgK)

W1 W2- capacitatea termica a agentului, W/K

-temp agentului cald la intrare si iesire

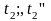-temp agentului rece la intrare si iesire

-entalpiea specifica agentului cald

-entalpiea agentului rece

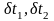-variatiea de temperature in aparat a agentului

Indicii: 1-pentru fluid cald . 2-pentru fluid rece . ‘-pentru intrare in aparat . ‘’-pentru iesire din aparat

La aparatele cu supra fata de incalzire plana, coef global de schimb de caldura se determina cu relatia:

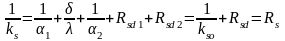in care:

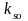- coef de schimb global de caldura al aparatului curat, W/( K)

- coef de schimb de caldura prin convectie de la agent la perete si invers, W/( K)

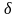- grosimea peretelui despartitor

Rsd1, Rsd2- rezistenta termica a depunirilor, ( K)/W

Rsd- rezistenta termica totala a depunirilor

Rs-rezistenta termica totala a aparatului cu depuneri

La aparatele tubulare, coef global de schim de caldura k se calculeaza cu expresia:

unde:

Pentru aparatele tubulare la care suprafaţa de schimb de căldură se exprimă, de regulă, casuprafaţă exterioară a ţevilor, coeficientul global de schimb de căldură raportat la aceastăsuprafaţă va fi

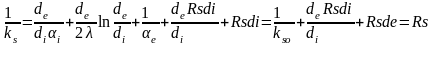
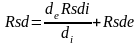
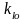-coef global de schimb de caldura al aparatului curat

-coef de schimb de caldura prin convectie intre agentul termic si peretele tevilor, W/( K)

- diametrul tevilor

Rsdi, Rsde-rezistenta termica a depunirilor pe peretele interior si exterior, ( K)/WR1-rezistenta termica totala a aparatului cu depuneri, raportata la lungimea tevilor, ( K)/W

40 .Radiatia termica prin ecrane

Pentru reducerea fluxului radiant se utilizează ecrane. Se con­sideră cazul cînd între cele două corpuri examinate anterior se dispune o foaie subţire de metal (ecran), iar ε₁=ε_ec= ε₂ = ε (ε_ec fiind gradul de absorbantă al ecranului). Conform relaţiei (2.120)

q_1ec= ε_rσ_o( )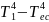

q_1ec2= ε_rσ_o( )

unde q_1ec şi q_2ec sînt densităţile fluxurilor rezultante de radiaţie transmise de la suprafaţa 1 la ecran şi respectiv de la ecran la suprafaţa 2, iar T_ec — temperatura absolută a ecranului.

Intrucît în condiţiile regimului staţionar qiec = qec2, rezultă că , iar

q_1ec=q_2ec=0,5 ε_rσ_{o .} Astfel în prezenţa unui singur ecran densitatea fluxului radiant se reduce de 2 ori. Se poate arăta că, în caz general, cînd ε₁≠ε₂≠ε_eci

q_ec/q₁₂=1/[1+ε_r (2/ε_eci-1)] (1.121)

unde qec e densitatea fluxului radiant în prezenta a n ecrane (i= 1, 2, 3,…,n).

Din expresia (2.121) rezultă că cele mai eficiente ecrane sînt acelea, care-s compuse din mai multe straturi şi care au grade de absorbantă reduse.

Particularitatile

1)Absorb si emit radiatia termica (gazelle cu 3 si mai multi atomi in molecula)

2)Radiatia gazelor este selective.

3)Gazele absorb si emit radiatia termica nu cu suprafata dar in volum.

S-grosimea stratului.

39 .Radiatia termica. Notiuni.

Radiatia reprezinta procesul de propagare a energiei sub forma de unde electromagnetice ce sunt generate de particulele elementare constitutive ale substantelor. Energia radianta este energia fotonilor sau a undelor electromagnetice emise de corp (sau mediu).

Radiatia poseda atitea proprietati ondulatorii, cit si proprietati corpuscular care, de altfel, nu se manifesta simultan. Procesul de propagare a radiatiei in spatiu are un character ondulatoriu, pe cind fenomenele de emisie , absorbtie si reflexie au un caracter corpuscular. Aceste proprietati se descriu de de ecuatii ale electrodinamicii si mecanicii cuantice. Radiatia se caracterizeaza prin lungimea de unda λ sau frecventa ν. O mare parte a corpurilor solide si a celor lichide (cu exceptia metalelor poleite) emit energia in toata gama lungimilor de unda. Din punctul de vedere energetic cel mai important rol in schimbatorul de caldura prin radiatie la temperaturi joase revine radiatiilor infrarosii. Aceste radiatii au aceeasi natra ca si celelalte radiatii si corespund lungimilor de unda 0,8*10^-6<λ<0,8*10^-3 m.

Energia emisa de corpuri creste brusc cu marirea temperaturii. De aceea in procesele care se desfasoara la temperaturi ridicate, rolul schimbului de caldura prin radiatie este destul de impportant. Radiatia termica nu e functie decit de temperatura corpului radiant si de proprietatile optice ale acestuia.

Intre procesele de conductivitate si convectie, examinate mai sus si cele de schimb de caldura prin radiatie exista o deosebire principala. Schimbul de caldura prin conductivitate termica sau prin convectie este indisolubil legat de existenta fie in corp, fie in mediu a unui cimp de temperatura. In procesele de schimb de caldura prin radiatie prezenta mediului continuu nu e obligatorie.

Undele electromagnetice, cazind pe corpurile inconjuratoare, sint partial absorbite de ele. Acum energia radianta se transforma in energie interna a corpului absorbant. Fractiunea de energie A absorbita de corp din toata energia incidenta a undelor electromagnetice se numeste capacitate de absorbtie a corpului, fractiunea de energie reflectata R – capacitatea de reflexie, iar fractiunea de energie D transmisa prin corp – capacitatea de transmisie. In conformitate cu legea conservarii energiei, A+R+D=1. Corpurile pentru care A=1, iar R=D=0, se numesc corpuri absolut negre, in caz cind D=1, iarA=R=0, corpurile se numesc absolut transparente sau diatermane. Pentru majoritatea corpurilor se poate considera D=0.

Legile radiatie termice

Densitatea fluxului radiant E reprezinta energia emisa prin radiatie intr-o unitate de timp de o suprafata a unui corp egala cu unitatea in toate directiile posibile ale semispatiului si constitue o caracteristica integrala ce se atribuie intregului interval de lungimi de unda. Densitatea spectrala a fluxului radiant E_λ=dE/dλ caracterizeaza repartitia energiei radiante in functie de lungimea de unda. Pentru corpul absolut negru dependenta lui E_o de lungimea de unda si de temperatura se stabileste cu legea lui Plannk:

(1)

U nde c₁=3,74ˑ10^-16 Wˑm²; c₂=1,439ˑ10^-2mˑK; T – temperatura absoluta a corpului radiant; n_r – indicele de refractie al mediului ce inconjoara corpul. In ce urmeaza se va considera n_r=1, pentru gaze n_r≈1, in vid n_r=1. Prin indicele 0 s-au notat marimile care se refera la corpul absolut negru.

Pe masura ce temparatura creste maximul dependentei E_λo=E_λo(λ) se deplaseaza spre lungimi de unda mai scurte (fig.2.20).

Cercetarea functiei (1) la extremitate a permis stabilirea dependentei λ_maxT=2,896ˑ10^-3 mˑK, denumita legea deplasarii a lui Wien.

Legea Stefan-Boltzmann se deduce in urma integrarii functiei

(2)

Unde σ_o=5,67ˑ10^-8 W/(m²K⁴) este constanta Stefan-Boltzmann.

Legile (1), (2) sunt juste numai pentru corpul absolut negru. Corpurile reale nu prezinta corpuri complet negre. Insa multe din ele pot fi considerate aproximativ corpuri cenusii, deoarece spectrul lor de radiatie este continuu si similar spectrului de emisie al corpului absolut negru. Pentru corpurile cenusii legea Stefan-Boltzmann are forma

E=εσ_oT₄

Legea lui Kirchhoff E/A=E_o. densitatea flixului radiant al corpului absolut negru E_o este functie numai de temperatura. Intrucit pentru corpurile cenusii A<1, inseamna ca totdeauna E<E_o. Din legea lui Kirchhoff reiese ca ε=A. Deoarece pentru corpurile solide netransparente A+R=1, rezulta ca corpurile, care reflecta bine energia radianta, absorb si emit putin. Pentru corpurile necenusii legea lui Kirchhoff se respecta numai la compararea caracteristicilor spectrale. Repartitia energiei radiante emise de un corp complet negru pe directii separate este neuniforma si se stabileste cu legea cosinusului a lui Lambert de forma

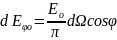
Unde E_ϕo reprezinta densitatea fluxului de radiatie corespunzator unghiului ϕ; dΩ – unghiul solid elementar, sub care din punctul dat al corpului radiant se vede pe suprafata emisferei, cu centrul in punctul dat al corpului radiant se vede pe suprafaţa emisferei, cu centrul în punctul dat, aria elementară; φ — unghiul cuprins între normala la suprafaţa ce radiază şi direcţia de emisie.

Valoarea maximă a lui Ev-: corespunde direcţiei normalei la suprafaţa corpului (φ = 0). Pentru corpurile reale legea lui Lambert se respectă doar aproximativ.