3 Закон пуассона

Закон Пуассона описывает массовые и редкие события, т.е. вероятность появления одного события очень мала. Применяется он при исследовании потока событий, т.е. последовательности событий, которые наступают в случайные моменты времени. Примерами потоков служат: прибытие автомобилей на станцию технического обслуживания, поступление автомобилей на текущий ремонт и т.п.

Для закона Пуассона вероятность появления х событий за время длительностью t определяется по формуле

,

(18)

где λ - интенсивность потока, т.е. среднее число событий, появляющихся в единицу времени;

х =0, 1, 2, 3, … - число событий, появляющихся за время t;

λt = а. - математическое ожидание числа событий, появляющихся за отрезок времени t.

Характерный признак закона Пуассона: математическое ожидание равно дисперсии и равно λt,

Рис. 3. Кривая закона Пуассона.

Схема, выравнивания опытных данных законом Пуассона.

1. Строим полигон относительных частот.

2. Вычисляем оценки математического ожидания М*(Х), дисперсии Д_В(х). Находим исправленное среднее квадратическое отклонение S(х) и среднее квадратическое отклонение среднего результата. Формулы для вычислений (1), (2), (3), (4), (5).

3. Если М*(х)=Д(х)=а, то можно считать, что опытные данные можно выравнивать законом Пуассона. Для окончательного принятия решения о законе распределения проводим проверку по критерию Пирсона. Вычисляем значения вероятностей по формуле (18) для вычисленного значения а, и х = 1, 2, 3, … к, используя таблицу приложения 3. Теоретические частоты определяем по формуле

,

По таблице приложения 2 по уровню значимости ά и числу степеней свободы d= k -2 находим значение χ²_набл.

4. Строим выравнивающую теоретическую кривую, откладывая по оси абсцисс значения х =0, 1, 2, 3, ... к, а по оси ординат - значения вероятностей р(х, а).

3 Логарифмически нормальный закон

Логарифмически нормальный закон имеет место в случае, если не сама случайная величина, а ее натуральный логарифм распределен по нормальному закону. Этот закон применяется при решении ряда технических задач. Например, ему подчиняются степенные износовые отказы изделий для некоторых условий.

Плотность вероятности для логиормального закона задается соотношением:

,

19

где а= М (lnХ) - математическое ожидание.

График плотности вероятности логнормального закона приведен на рис. 4.

Рис. 4. График плотности логнормального закона распределения.

Схема выравнивания опытных данных логнормальным законом распределения аналогична приведенной при обработке нормального закона распределения.

4 Закон распределения вейбулла

Закон распределения Вейбулла применяет в задачах, связанных с длительностью жизни технических изделий. Например, длительность исправного состояния технических изделий при износовых отказах.

Плотность вероятности закона Вейбулла имеет вид:

,

20

где n, μ - параметры закона распределения;

х - аргумент, в общем случае его роль играет время. Выражение (20) можно преобразовать, обозначив

,

Тогда

,

21

Значения плотности вероятности закона Вейбулла, записанных в форме (21) табулированы. Таблица приведена в приложении 5.

Параметры n и μ связаны с числовыми характеристикам закона и вычисляются с помощью гамма-функции.

Доказано, что параметр n есть функция коэффициента вариации, который вычисляется по формуле

,

22

Зная коэффициент вариации, по таблице приложения 6 определяем параметр n. Параметр μ определяем из выражения для математического ожидания:

,

23

где - гамма-функция, определяемая по таблице приложения 8.

Зная значение μ определяем а=1/ μ.

График плотности распределения закона Веибулла приведен на рис. 5.

Схема выравнивания опытных данных законом Вейбулла.

1. Строим гистограмму относительных частот.

2. Вычисляем М*(х), Д_В(х), σ_В(х), σ_М*(х) по формулам (1), (2), (3), (5).

3. Находим коэффициент вариации по формуле (22) и по таблице приложения 8 определяем значение параметра n.

4. По формуле (23) вычисляем значение параметра μ и а =1.

5. Проверку правдоподобности принятой гипотезы о принадлежности экспериментальных данных к закону Вейбулла проводим по критерию Пирсона.

Теоретические частоты вычисляем по формуле

,

Вероятность Pi попадания замера в частичный интервал вычисляем по формуле

,

24

или

,

25

По таблице приложения 5 по уровню значимости ά и числу степеней свободы d = k -3 определяем χ²_табл.

С целью решения проблем повышения безопасности и надежности автомобилей необходимо обосновать возможность строительства станции дорожной диагностики СДД на дороге с интенсивностью движения 12 тыс. автомобилей в сутки, а также разработать устройство для контроля состояния шин.

Для достижения поставленной цели должны быть решены следующие задачи:

- изучение характера входного потока автомобилей на СДД;

- изучение распределения времени диагностирования;

- исследование соответствия давления воздуха в шинах эксплуатируемых автомобилей требованиям технических условий.

Рассмотрим каждую из перечисленных задач.

1. Изучение характера входного потока автомобилей на СДД.

Для расчета станции необходимо использовать системы массового обслуживания СМО, что позволяет произвести оптимизацию числа постов и расстановки рабочих на постах, а также выделить основные и дополнительные посты дня пиковых нагрузок, однако аппарат СМО можно использовать только в том случае, когда входной поток на станцию описывается законом Пуассона. Поэтому приводят исследование состояния автомобилей на дороге. Выявляется неисправности тормозной системы, рулевого управления и освещения, при этом проводится опрос водителей неисправных автомобилей и фиксируются случаи, в которых водители указанных автомобилей хотели бы, посетить станцию диагностики. Исследование проводилось с 8.00 до 11.00 в течение недели. Часы проверки выбраны по наибольшей интенсивности движения в указанное время суток. Было зафиксировано 300 автомобилей имеющих неисправности, водители этих автомобилей хотели бы посетить станцию диагностики. Получены следующие данные.

Таблица 3

Разряды (число автомобилей которые могли бы посетить станцию с 8.00 до 11.00)	0	1	2	3	4	5	6	7	8
Опытные частоты попадания в разряды	10	46	72	78	53	25	10	4	2

Необходимо исследовать экспериментальные данные и проверить принятую статистическую гипотезу о том, что входной поток на СДД описывается законом Пуассона. Допускается ошибка 5%.
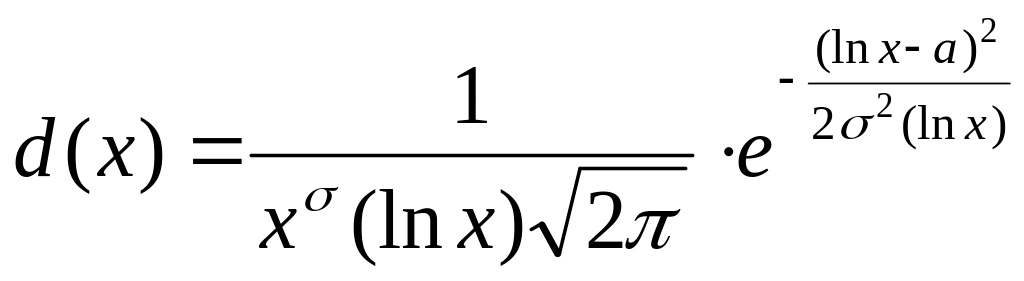