5. Обчислення окремих власних значень

Якщо потрібно обчислити лише деякі з власних значень (наприклад, або ), то найпростіше використати степеневий метод для формування послідовності векторів

(16)

Нехай матриця А має n лінійно незалежних векторів і максимальне за величиною власне значення таке, що .

Якщо розкласти деякий ненульовий вектор за базисом власних векторів матриці

,

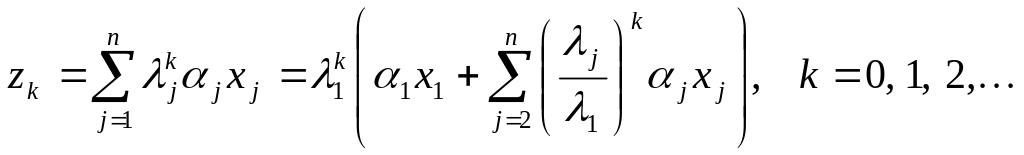
Оскільки для , напрям вектора прямує до напряму власного вектора , якщо тільки .

Для підвищення стійкості обчислень проводять масштабування послідовності векторів , яке найпростіше здійснити , якщо перейти до послідовності нормуванням векторів за значенням їх найбільших елементів , тобто замість виразу (19) використовувати співвідношення:

, , (17)

при цьому

(18)

і похибка обчислення найбільшого власного значення прямує до нуля як .

Якщо степеневий метод застосувати до оберненої матриці , то аналогічно можна оцінити величину мінімального власного значення , якщо виконується умова . При цьому мінімальне власне значення матриці А обчислюється за формулою

, де – максимальне за модулем власне значення матриці .

Приклад 6. Знайти наближене значення максимального і мінімального за модулем власних значень матриці

.

На лістингу 7 наведено результати обчислень степеневим методом після першої, другої та двадцятої ітерації. Для обчислення максимальної компоненти власного вектора складена функція користувача .

На лістингу 8 наведено програму, яка обчислює найбільше або найменше за модулем власні значення степеневим методом із заданою точністю. Одержані результати співпадають з результатами, одержаними за допомогою програми Mathcad.

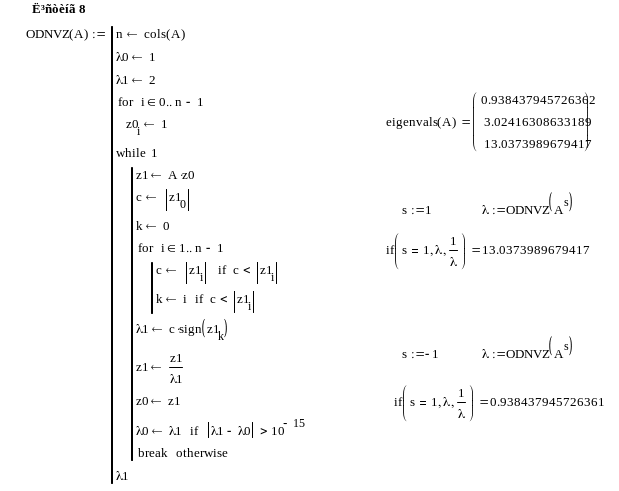
6. Метод Данилевського

Метод Данилевського є досить простим і зручним методом для знаходження як характеристичного многочлена, так і розв’язання повної проблеми власних значень матриці. Розглянемо ідею метода.

Нехай маємо квадратну матрицю 3-го порядку

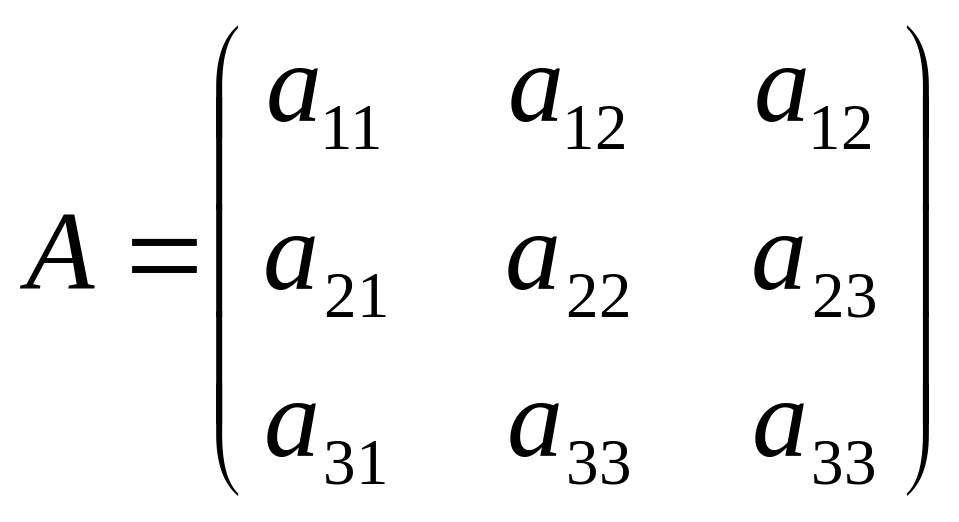, (19)

для якої знаходиться характеристичний многочлен за допомогою подібних перетворень матриці А на матрицю вигляду

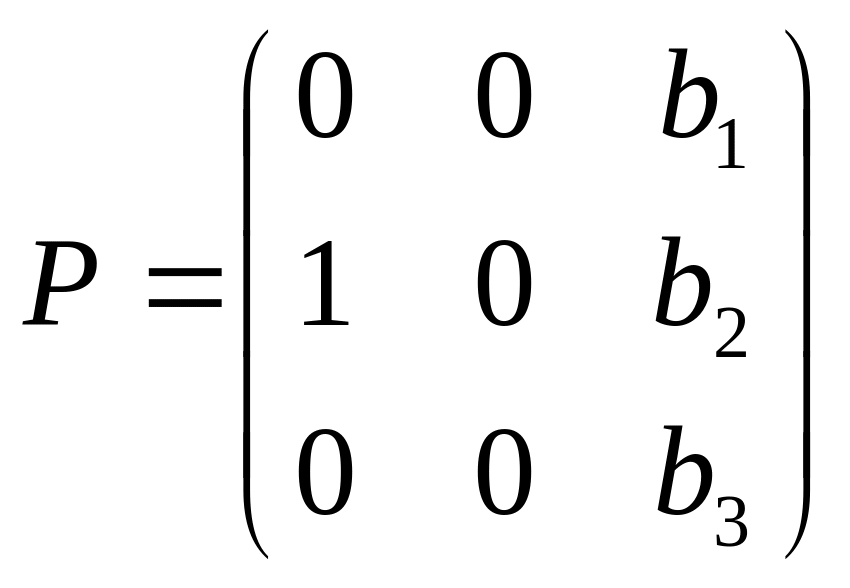, (20)

яка має нормальний вигляд Фробеніуса, тобто матриця має у явному вигляді в останньому стовпці шукані коефіцієнти характеристичного рівняння. Оскільки подібні матриці мають один і той же характеристичний многочлен, то виконуються рівності

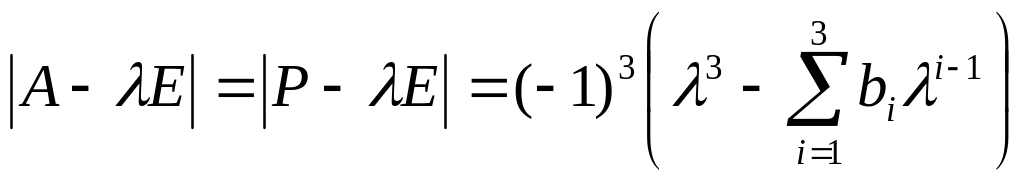. (21)

В цьому легко переконатися безпосередньо:

.

Подібні перетворення матриці А до матриці Р здійснюються послідовно. На першому кроці матриця А перетворюється на подібну до неї матрицю , в якій передостанній стовпець має необхідний вигляд. На другому кроці матриця перетворюється на подібну до неї матрицю , в якій уже два передостанні стовпці мають необхідний вигляд, і т.д.

Для матриці 3-го порядку, на першому кроці матриця А множиться справа на матрицю вигляду

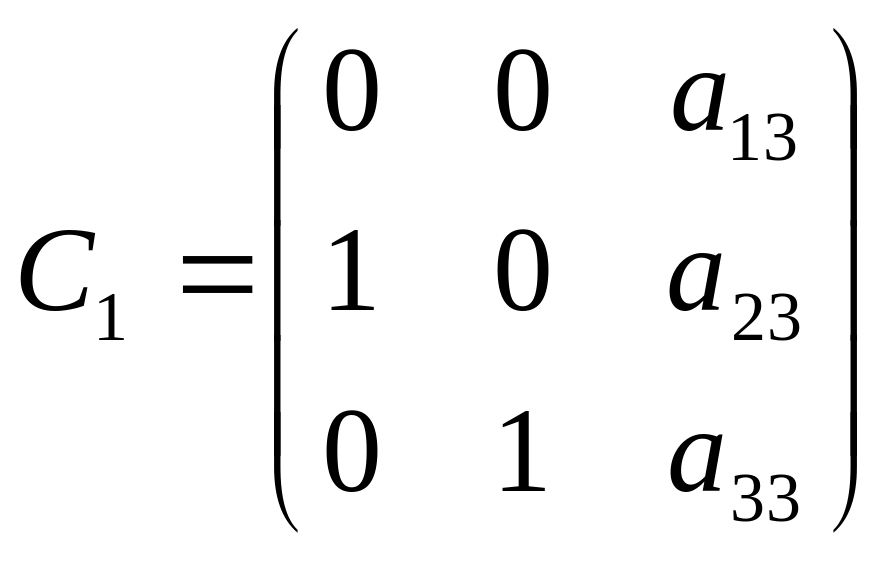(22)

і зліва на матрицю, обернену до неї

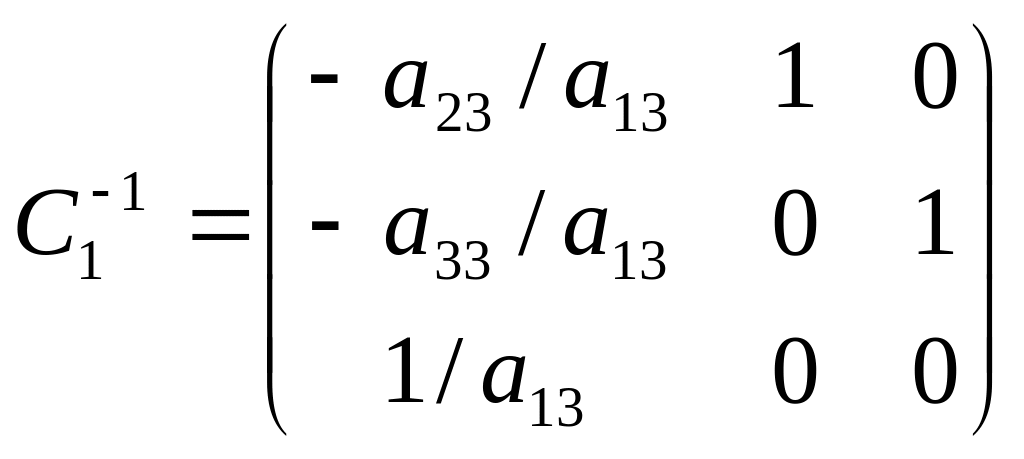. (23)

Легко перевірити, що

. (24)

На другому кроці матриця множиться справа на матрицю вигляду

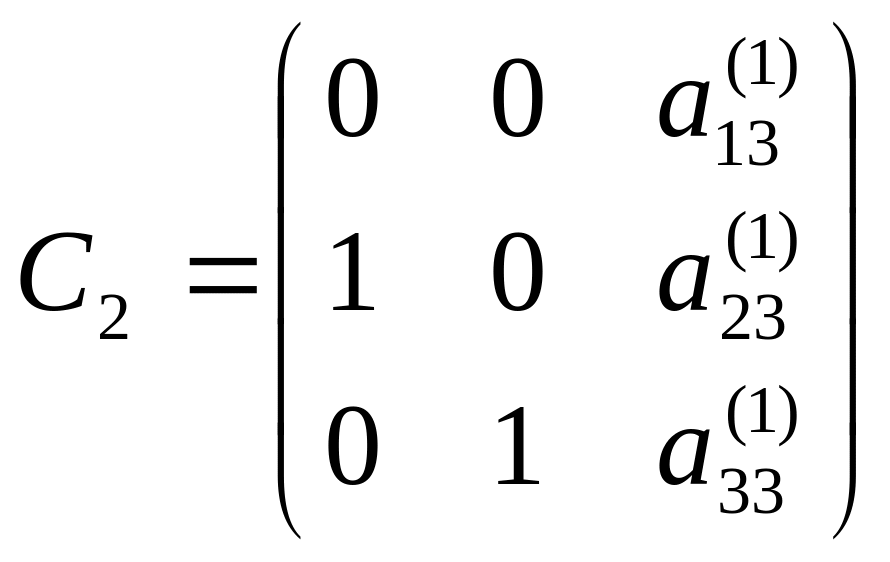(25)

і зліва на матрицю, обернену до неї

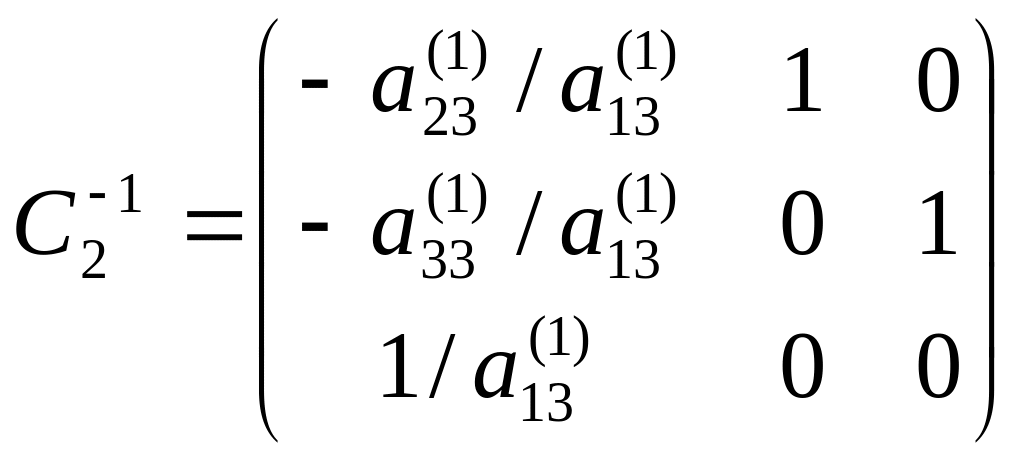. (26)

Легко перевірити, що матриця буде мати потрібний вигляд

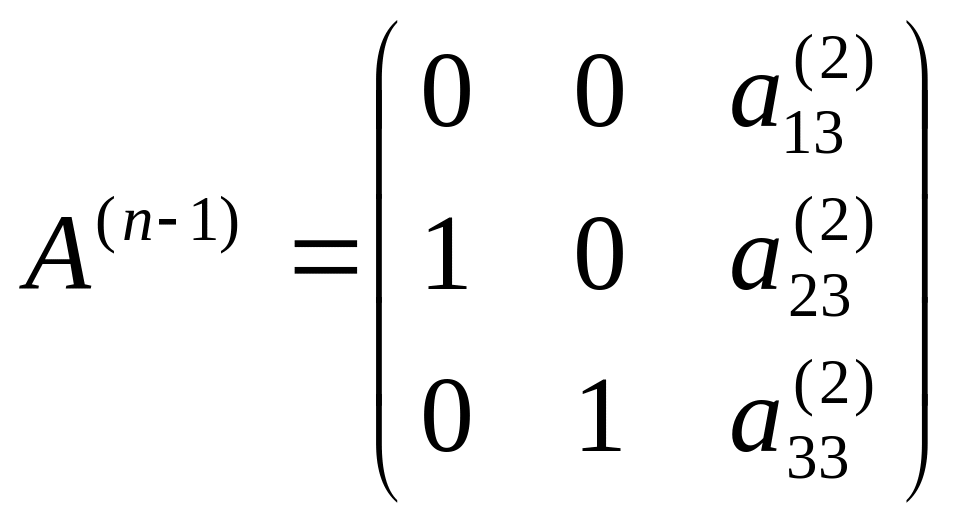, (27)

що має нормальну форму Фробеніуса та подібна до вихідної матриці А.

При описаних вище перетвореннях може трапитись, що елемент . Тоді продовжувати процес у такому вигляді не буде можливим. При цьому можуть бути два випадки.

1. Серед елементів останнього стовпця є хоча би один, відмінний від нуля, наприклад, елемент . Тоді для продовження процесу потрібно поміняти і-й і к-й рядки і продовжити процес.

2. Усі елементи останнього стовпця дорівнюють нулю. Тоді матриця має вигляд

,

де F – квадратна матриця порядку , яка має нормальний вигляд Фробеніуса, а матриця – квадратна матриця порядку і має місце рівність

,

з якої знаходимо власні значення матриці , а отже, і матриці А.

Приклад 7. Для матриці, заданої в прикладі 7 обчислити власні значення методом Данилевського.

Результати обчислень наведено на наступному лістингу 8.