Практична робота №2
Мета роботи: Вивчення методів обчислення власних значень і власних векторів матриць і набуття навичок їх реалізації за допомогою математичного пакету програм Mathcad.
Зміст роботи:
1. Вивчити можливості математичного пакету Mathcad для розв’язання повної та часткової проблеми власних значень та власних векторів матриці.
2. Виконати запропоновані завдання з використанням засобів пакету Mathcad. Зміст звіту:
Навести короткі теоретичні відомості, постановку завдань та результати їх виконання.
Короткі теоретичні відомості
Усі методи обчислення власних значень і власних векторів матриці можна розділити на дві групи: прямі та ітераційні. До першої групи методів належать методи, що базуються на обчисленні коренів характеристичного рівняння матриці. До цієї групи відносяться методи: характеристичного рівняння матриці, Фадєєва-Лавер’є, Крилова та ін. Їх, як правило, застосовують у випадку матриць невеликої розмірності. До другої групи відносяться методи, що використовують ортогональні перетворення подібності і зводять матрицю до блочно-діагонального вигляду з блоками першого і другого порядків. Серед таких методів слід відмітити ітераційний метод обертання або QR-алгоритм. Сюди ж можна віднести також степеневий метод і різні його модифікації.
Метод характеристичного рівняння матриці
Як відомо, характеристичне рівняння матриці має вигляд
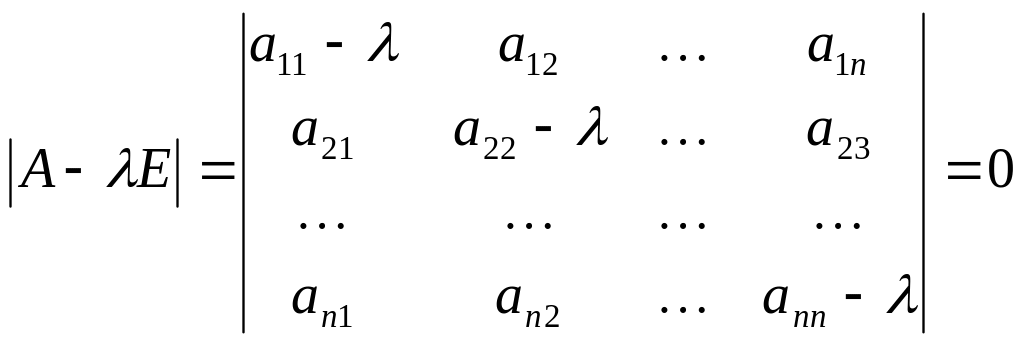, (1)
де Е – одинична матриця.
Якщо
визначник (1) розкрити відносно
,
то отримаємо так зване характеристичною
рівняння матриці А
у вигляді полінома n
–степеня
.
Розв’язок цього рівняння визначає
множину всіх власних значень матриці.
Кожному власному значенню матриці
відповідає свій власний вектор. З цього
випливає, що квадратна матриця розмірності
має n
власних значень і власних векторів.
Задача про знаходження усіх власних
значень і відповідних власних векторів,
називається повною
проблемою власних значень,
на відміну від задачі, коли потрібно
зайти одне або декілька власних значень,
яка називається частковою
проблемою власних значень.
Для розв’язання повної проблеми власних значень та власних векторів матриці в пакеті Mathcad є ряд вбудованих функцій. Зокрема, функція eigenvals(A) дає можливість обчислити усі власні значення матриці, функція eigenvecs(A) дає можливість обчислити усі власні вектори матриці, функція eigenvec (A, λ) дає можливість обчислити власний вектор матриці, що відповідає заданому власному значенню. Крім цього, пакет Mathcad дає можливість безпосередньо розкривати характеристичне рівняння і знаходити його корені (власні значення). Для цього може бути використаний оператор solve (розв’язати) панелі Symbolic, обчислювальний блок Given – Find (Дано – знайти) та функція polyroots(v), яка повертає вектор усіх корені алгебраїчного рівняння, де v – вектор коефіцієнтів рівняння. Приклад 1. Обчислити власні значення і власні вектори матриці
.
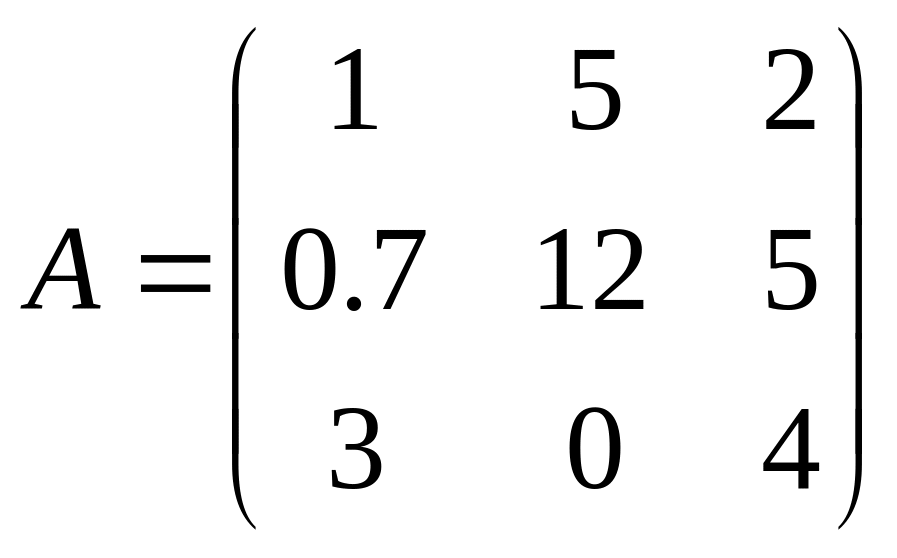Результати обчислень наведено на наступному лістингу 1
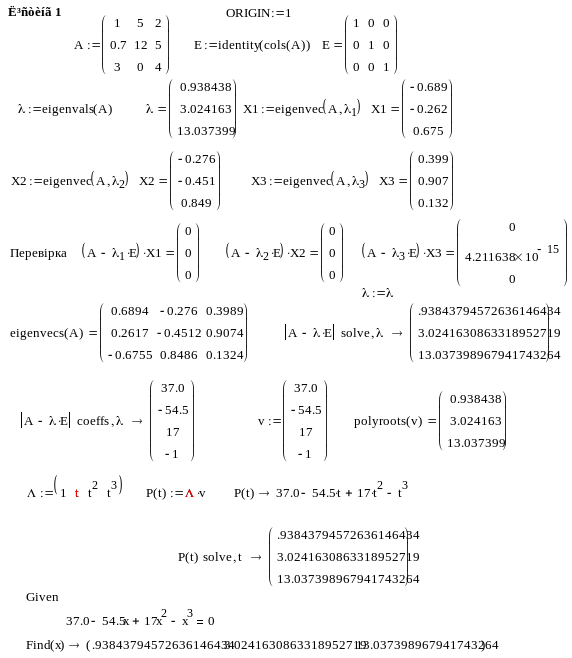
Метод Фадєєва-Левер’є
Для обчислення коефіцієнтів характеристичного рівняння крім прямого розкриття самого визначника (див. приклад 1) існує декілька методів, серед яких виділяється метод Фадєєва-Левер’є, за допомогою якого обчислюються:
коефіцієнти характеристичного полінома
; (2)
обернена матриця
; (3)
резольвента матриці
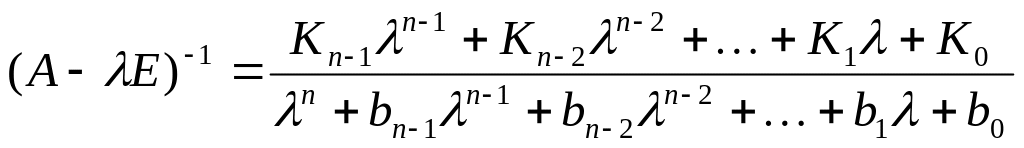. (4)
Метод
Фадєєва-Левер’є базується на результатах
обчислення слідів матриці А
і добутків матриць
,
де
– коефіцієнти чисельника резольвенти
матриці (4). Коефіцієнти чисельника і
знаменника виразу (4) визначаються
ітераційно (спочатку коефіцієнти
чисельника
,
а потім коефіцієнти знаменника
відповідно до наведеного нижче алгоритму:
,
;
,
;
… … … … … … … … … … … …
,
;
… … … … … … … … … … … …
,
,
де Е
– одинична матриця,
– слід матриці. Умова перевірки
правильності виконання алгоритму має
вигляд
.
Приклад 2. Побудувати характеристичне рівняння матриці, заданої в прикладі 1 та знайти його корені (власні значення)
Ілюстрація алгоритму розв’язання задачі методом Фадєєва-Левер’є за допомогою програми Mathcad наведено на лістингу 2
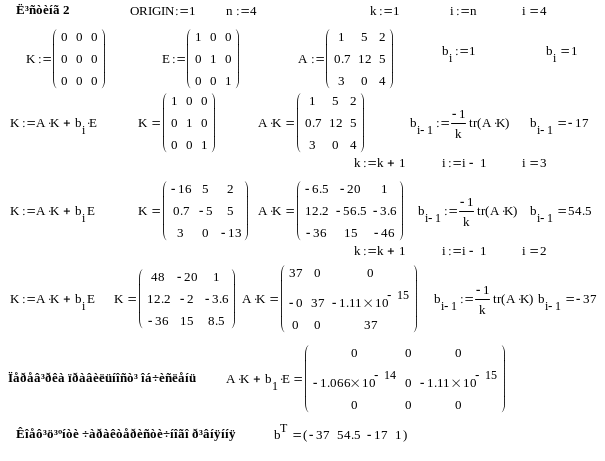
Як бачимо, одержані коефіцієнти характеристичного рівняння матриці співпадають з коефіцієнтами, одержаними іншими методами.
На лістингу 3 наведено програму реалізації методу Фадєєва-Левер’є за допомогою Mathcad
