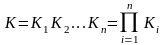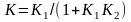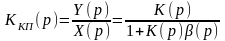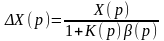- •Егер кері байланыс байланыс оң болса, онда
- •Тура тізбекте үш буын орналасқан жағдайдағы беріліс функциясы
- •Егерде төмендегі қатынастарды еске алсақ
- •Шығыстық шаманың кескіні бұл жағдайда былайша жазылады
- •4.1 Сур. Өзекті дилатометр
- •4.2 Сур. Биметалды термометр
- •4.3 Сур. Манометрлік термометр
- •Студенттердің өзіндік жұмысына арналған тақырыптар тізімі.
- •1. Қандай аспаптың жұмыс принципі зерттелетін ортада қалтқыға әсер ететін итергіш күш шамасын не оның бату тереңдігін өлшеуге негізделген.
- •11.1 Сур. Кондуктометрлік лшеу схемасы
- •Студенттердің өзіндік жұмыстарының үлгілік тізімі (сөж)
1-ДӘРІС
НЕГІЗГІ ТҮСІНІКТЕМЕЛЕР МЕН АНЫҚТАМАЛАР
Өлшеу деп, арнайы өлшеу құралдарының жәрдемімен физикалық шамалардың мәндерін тәжірибе жүзінде анықтауды атайды.
Өлшеу қателігі деп, өлшеу нәтижесінің өлшенетін шаманың нақты мәнінен ауытқуын айтады. Өлшеу қателігі өлшеу дәлдігінің тікелей сипаттамасы болып табылады.
Өлшеу дәлдігі деп, өлшенетін физикалық шаманың нақты мәні мен өлшеу нәтижесінің өзара жуықтау дәрежесін айтады.
Өлшеу құралдары (ӨҚ) деп, дәлдік сипаттамалары нормаланған, өлшеу тәжирибелерінде қолданылатын техникалық жабдықтарды айтады.
Өлшеу тәсілі деп, өлшеу құралдарын және принциптерін қоолдануды қамтитын айлалардың жиынтығын айтады.
Өлшеу принципі деп, өлшеудің негізін анықтаушы түрлі физикалық құбылыстарды атайды. Мысалы, температураны өлшеуде термоэффект құбылысын қолдану.
Өлшеу түрлерін төрт топқа бөлуге болады: тура, жанама, жиынтықты ( совокупные) және біріккен ( совместный).
Тура өлшеуде өлшенетін шаманы тәжірибе нәтижесінен тікелей анықтайды у=х, мұндағы у- өлшеу құралының шығыстық шамасы.
Жанама өлшеуде өлшенетін шаманы анықтау үшін, сол шамамен функционалдық байланыста жатқан параметрлер тура тәсілмен өлшенетін, өлшеу нәтижелері бойынша өлшенетін шама есептеліп анықталады. Өлшеу теңдеуін келесі түрде жазуға болады у = F (х1, х2, .... хn), мұндағы у өлшенетін шама, F – функционалдық байланыс, х1, х2, .... хn тура өлшеу арқылы табылатын параметрлер.
Жиынтықты өлшеуде аттас шамаларды бір мезетте өлшеу орын алады. Нәтижесінде теңдеулер жүйесі құрылып, өлшенетін шамаларды теңдеулер жүйесін шешу арқылы табады.
Біріккен өлшеуде, әртекті шамаларды бір мезетте өлшеу орын алады. Мысалға, келесі функционалдық байланыс Rt=R0(1+λt+βt2), белгілі болсын, мұндағы Rt кез келген t температурасындағы кедергінің мәні, R0 температура t=0 болғандағы кедергінің мәні, λ және β тұрақты коэфиценттер. Функционалдық байланыстарды қолдана отырып, R0, λ және β мәндерін анықтау қажет. Ол үшін, температураның үш мәнінде t1, t2 и t3 сәйкесінше кедергілердің мәндері Rt1, Rt2, Rt3 өлшеніп алынады. Өлшеу нәтижелерін пайдалана отырып, теңдеулер жүйесін құрып, оны шешу арқылы ізделініп отырған шамаларды анықтаймыз.
R0(1+λt+βt2)- Rt1=0
R0(1+λt+βt2)- ,Rt2 =0
R0(1+λt+βt2)- Rt3=0
Сонымен қатар, статикалық өлшеу ( кірістік өлшенетін шама уақыт бойынша өзгермейді) және динамикалық өлшеу ( өлшенетін шама уақыт бойынша өзгеріп отырады) түрлері де кездеседі.
Қазіргі таңда келесі өлшеу тәсілдері кездеседі: тікелей бағалау, өлшеммен салыстыру, дифференциалдық, нольдік, алмастыру(замещения) және сәйкестік (совпадения).
Тікелей бағалауда өлшеу нәтижесі өлшеу құралдарының тікелей көрсетулерімен анықталады. Бұл тәсілдің дәлдігі төмен.
Салыстыру тәсілінде өлшенетін шаманың уақыттың бір мезгілдерінде немесе әрбір тәжрибеде белгілі өлшеммен салыстырылып отырылады. Салыстыру нәтижесі салыстырушы құрылғы жәрдемімен бағаланады. Мысалы, массаны гир жәрдемімен анықтау.
Дифференциалдық тәсілде өлшеу құралының кірісіне өлшенетін шама мен белгілі өлшемнің арасындағы айырым беріледі. Бұл тәсіл дәл тәсілдер қатарына жатады.
Нөлдік тәсілде салыстыру құрылғысының көмегімен , өлшенетін шама мен белгілі өлшемнің арасындағы айырым нөлге дейін жеткізіледі.
Алмастыру тәсілінде өлшенетін шама өзінің белгілі шамасымен алмастыру арқылы табылады.
Егер
өлшенетін шаманың мәні сәйкестендірілетін
шаманың бағалық бөліктерінен (цена
деления) артық болып жатса, онда сәйкестік
тәсіл (нониус тәсілі) қолданылады. Бұл
тәсілде бағалық бөліктер әртүрлі болып
келетін екі шама қолдалынады. Мысалға,
бірінші шаманың бағалық бөлігі
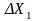 болсын,
ал өлшенетін шама
болсын,
ал өлшенетін шама

 болсын.
Бұл жағдайда бағалық бөлігімен
салыстырғанда қіші болып келетін екінші
шама
болсын.
Бұл жағдайда бағалық бөлігімен
салыстырғанда қіші болып келетін екінші
шама
 қолданылады.
қолданылады.
Егер сезімталдықты n рет көтергіміз келсе, онда бағалық бөліктердің арасында келесі қатынас орын алуы керек.
∆х2=∆х1(1-1/ n)
Өлшеу кезінде, өлшенетін шаманы ∆х аспаптың нөлдік белгілерінің арасына орналастырып, Ν- санын табады. Бұл сан екі шаманың бағалық бөліктерінің өзара сәйкес келетін цифрларына тең. (1.1- сурет)

бірінші өлшем
1.1- сурет Өлшеудің
нониустық тәсілі
екінші өлшем
Бұл жағдайда келесі қатынас тура
Ν ∆х1= ∆х+ Ν ∆х2
Бұдан
∆х= Ν(∆х1 _-_∆х2)= Ν∆х1/n , яғни n- нің мәні көбейген сайын, сезімталдық жоғары. Жалпы жағдайда кез-келген өлшеу тәсілін өлшенетін ақпараттардың біртіндеп түрлену процессі ретінде қарастыруға болады. Әдетте түрлендірудің тура және теңгеру тәріздес тәсілдері кездеседі.
Тура түрлендіру тәсілдерінде кірістік сигнал тұйықталмаған тізбек бойынша барлық түрлендіргіштерден біртіндеп өтіп, шығыста орналасқан санақ құрылғысы арқылы өлшеу нәтижесі бағаланады. Бұл тәсілде ақпарат бір бағытта ғана жүреді. Мұндай өлшеу құралының қателігі, құрал құрамына кіретін түрлендіргіштердің қателіктерімен айқындалады.
Түрлендірудің теңестендіру тәсілінде, құрылғы құрамына ең құрығанда екі түрлендіру каналы болуы керек, яғни тура және кері. Тура түрлендіру каналының шығыстық шамасы өлшеу нәтижесін көрсету аспаптарына беріледі, сонымен қатар кері түрлендіру каналының кірісіне өлшенетін шаманың және кері түрлендіру каналының шығыстық мәнінің арасындағы айырым түседі. Мұндай түрлендіру тәсілінде қорытқы қателік тек кері түрлендіру каналының қателігімен айқындалады, тура түрлендіру каналының қателікке қосатын үлесін ескермесе де болады.
Өлшеу құралдарының жіктелуі мен сипаттамалары.
Өлшеу тәсілдерін жүзеге асыру үшін түрлі өлшеу құралдары қолданылады: өлшем, өлшеу түрлендіргіші, өлшеу аспабы, қосалқы жабдықтар, өлшеу ақпараттық жүйелер.
Өлшеу түрлендіргіштері - өлшеу ақпараттарының сигналдарын қадағалауға, қашыққа беруге, өңдеуге, сақтауға және ЕЭМ – на енгізуге қолайлы түрде түрлендіріп беруге негізделген құрал. Өлшеу түрлендіргіштері келесі негізгі топтарға бөлінеді: алғашқы түрлендіргіш, аралық түрлендіргіш және беру (передающие) түрлендіргіштері.
Алғашқы түрлендіргіштерге өлшенетін шама беріледі. Бұл түрлендіргіш өлшенетін физикалық шамаларды ары қарай түрлендіруге қолайлы формада түрлендіріпм береді.
Аралық түрлендіргіш алғашқы түрлендіргіштен кейін орналасады да, сигналдарды күшейту, түзету т.с.с түрлендіргіштер жүргізіледі.
Беру түрлендіргіштері өлшеу ақпараттарының сигналдарын қашықтыққа беруге негізделген.
Түрлендіргіштер тұтыну энергиясына қарай, кірістік және шығыстық сигналдардың түрлеріне қарай электрлік, гидравликалық, пневматикалық, электрлық-пневматикалық т.с.с. болып бөлінеді.
Өлшеу аспаптары ақпараттық сигналдарды бақылаушыларға тікелей бақылауға лайықты түрде алуға негізделген. Бұл аспаптар аналогтық және цифрлық болып жіктеледі және де көрсеткіштік, тіркеуші, интегралдаушы, қосқыш аспаптары түрінде де кездеседі.
Қосалқы құралдарға түрлі шунттар, кабелдер, қорек көздері т.с.с. жабдықтар жатады. Қосалқы құралдар өлшеу құралдарының метрологиялық сипаттамаларына әсерін тигізеді, сол себептен оларда нормаланады.
Өлшеу – ақпараттық жүйелері ақпараттарды автоматты түрде өңдеп, түрлендіріп, басқару, реттеу жүйелеріне қолдануға лайықты түрде беруге негізделген. Өлшеу – ақпараттық жүйелері қолданыс түрлеріне қарай келесі жүйелерге бөлінеді: өлшеу жүйелері, түрлері объектілердің сандық сипаттамаларын алуға негізделген; бақылау жүйелері, объект параметрлерінің қойылған талаптар мен нормаларға қаншалықты сәйкес келетіндіктерін анықтауға негізделген; диагностика жүйелері, объектлердегі ақаулардың себептерін анықтап, оларды жою мәселелеріне негізделген.
Қазіргі кезде өлшеу құралдарының тиімділігін келесі сипаттамалалар арқылы бағалайды: дәлдігі, шапшаңдығы, сезімталдығы, сенімділігі.
Дәлдігі - өлшеу нәтижесінің өлшенетін шаманың нақты мәніне жуықтай дәрежесін сипайды. Кей жағдайларда «қателік» деген ұғым қолданылады. Қателік өлшеу нәтижесі мен шынай мәннің арасындағы алшақтық дәрежесін сипаттайды. Қателіктің келесі түрлері кездеседі.
Абсолюттік қателік
∆=y-xд;
салысьырмалы қателік (%) δ=(∆/xд.)∙100%;
келтірілген
қателік δпр=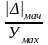 ; мұндағы
у - өлшеу құралының көрсетуі, Х
; мұндағы
у - өлшеу құралының көрсетуі, Х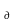 - өлшенетін шаманың нақты мәні,
- өлшенетін шаманың нақты мәні,
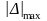 -абсолюттік қателіктің максималдық
мәні, У
-абсолюттік қателіктің максималдық
мәні, У - өлшеу аспабы шкаласының максималдық
мәні.
- өлшеу аспабы шкаласының максималдық
мәні.
Егер өлшеу құлалының қателігі қалыпты эсплуатациялау кезінде сыртқы ортаның параметрлері номиналдық мәндерінен ауытқыған жағдайда пайда болған қателікті қосымша қателік деп атайды.
Өлшеу құралының шапшаңдығы бірлік уақыт ішіндегі жүргізілетін өлшеу сандарымен сипаттайды.
Өлшеу құралының сезімталдығы аспаптың шығыстық У және кірістік Х шамаларының қатынысымен сипатталады.
S=dy/dx
Стрелкалы аспаптар үшін S= α /x . Өлшенетін шама х = 1 / S∙ α
Мұндағы α - аспаптың көрсетуі, 1 / S – бағалық бөлік (аспап тұрақтысы).
Өлшеу құралдарының сипаттамаларына сонымен қатар өлшеу диапазондары, кірістік кедергілері, габариттері, массалары, бағалары т.с.с. жатады.
1-дәріс бойынша тест сұрақтары
1. Өлшеу әдісі бұл -
А) физикалық құбылыстар мен заңдылықтар жиынтығы.
В) өлшеу қателіктері мен нәтижелерінің жиынтығы.
С) есептік және тіркеу құрылғысының жиынтығы.
D) өлшеу құрылғысының статикалық және динамикалық сипаттамасының жиынтығы.
+Е) өлшеу құрылғысының және принциптерінің қолдану әдістерінің жиынтығы.
2. Физикалық шамалардың мәнін анықтауға арналған және нормаланған дәлділік сипаттамасы бар техникалық құрылғының жиынтығы нені көрсетеді?
+А) өлшеу құрылғысы
В) өлшеу техникасын
С) өлшеу объектісі
D) автоматты бақылау жүйесі
Е) автоматты реттеу жүйесі
3. Өлшенетін шаманың шынайы мәннен ауытқыған өлшеу нәтижесін қалай атаймыз?
А) өлшеу дәлдігі
+В) өлшеу қателігі
С) өлшеу нәтижесі
D) өлшеу саны
Е) барлық көрсетілген жауап дұрыс
4. Физикалық шамалардың мәнін анықтауға арналған және нормаланған дәлділік сипаттамасы бар техникалық құрылғының жиынтығы нені көрсетеді?
+А) өлшеу құрылғысы
В) өлшеу техникасын
С) өлшеу объектісі
D) автоматты бақылау жүйесі
Е) автоматты реттеу жүйесі
5. Физикалық шаманы өлшеу арқылы табылған аталған санды қалай айтамыз?
А) өлшеу дәлдігі
В) өлшеу қателігі
+С) өлшеу нәтижесі
D) өлшеу саны
Е) барлық көрсетілген жауап дұрыс
2-ДӘРІС
ӨЛШЕУ ҚАТЕЛІКТЕРІ
Өлшеу қателіктері әдетте түрлі факторлардың әсерінен орын алады да, негізінен екі топқа бөлінеді: кездейсоқ және систематикалық.
Егер де бір шаманы бірнеше қайталап өлшеу барысында орын алған қателіктер тұрақты мән алса, немесе белгілі бір заңдылықпен өзгерсе, онда ондай қателікті систематикалық қателік деп атайды. Систематикалық қателік өлшемінің номиналдық мәнінің өзгеріске ұшырап кету салдарынан туындайды. Систематикалық қателік сонымен қатар өлшеу тәсілдерінен кететін қателік, (тәсілдік қателік) өлшеу құралдарының конструктивтік кемшіліктерінен, олардың сипаттамларының өзгеріске ұшырауынан, оператордың өлшеуді дұрыс жүргізбеу салдарынан да туындайды.
Систематикалық қателіктер өз кеегінде тұрақты және айнымалы болып бөлінеді. Тұрақты қателіктер аспап стрелкаларының қисаю салдарынан, аспаптарды дұрыс емес градуиовкалау т.с.с. салдардан туындайды.
Айнымалы қателіктердің ішінен прогрессті түрде өзгермелі, монотонды өспелі немесе кемімелі, периодты түрде өзгермелі қателіктерді атап өтуге болады. Систематикалық қателіктерді аспаптарға сәйкескенше түзетулер енгізу, компенсациялау т.с.с. тәсілдерді қолдану арқылы жоюға болады.
Ө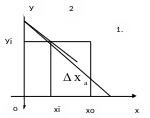 лшеу
құралдарына түрлі факторлар әсер ету
салдарынан, оның сипаттамасы өзгеріске
ұшырауы мүмкін. Бұл жағдайда аддитивті
(2.1- сурет), мультипликативті (2.2- сурет)
және бейсызықты қателіктер (2.3- сурет)
орын алуы мүмкін.
лшеу
құралдарына түрлі факторлар әсер ету
салдарынан, оның сипаттамасы өзгеріске
ұшырауы мүмкін. Бұл жағдайда аддитивті
(2.1- сурет), мультипликативті (2.2- сурет)
және бейсызықты қателіктер (2.3- сурет)
орын алуы мүмкін.
2.1-сурет. Аддитивті қателік ∆ ха 1 – идеал сипаттама, 2 – аддитивті қателігі бар сипаттама
Кездейсоқ қателіктерді сипаттау.
Кездейсоқ қателіктерді сипаттау үшін «таралымның дифференциялдық функциясы» деген ұғым енгізілді.
Қалыпты заңдылық (Гаусс заңдылығы) үшін бұл функция былайша жазылады.
–(х-m)2/2δ2х
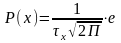
Мұндағы
m – өлшенетін кездейсоқ шаманың X –
математикалық күтімі, T
 -
кездейсоқ шаманың Х орта квадраттық
ауытқуы.
-
кездейсоқ шаманың Х орта квадраттық
ауытқуы.

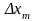
2 .2-
сурет. Мультипликативті қателік ∆ хм.
1 – идеал сипаттама, 2 – мультипликативті
қателігі бар сипаттама.
.2-
сурет. Мультипликативті қателік ∆ хм.
1 – идеал сипаттама, 2 – мультипликативті
қателігі бар сипаттама.
2.3- сурет. Бейсызықтық қателік ∆ хн. . 1 – идеал сипаттама, 2 – бейсызықтықтан болатын қателік.
Қалыпты заңның дифференциялдық функциясы 2.4- суретте келтірілген, әдетте сурет ауданы


2.4- сурет. Кездейсоқ қателіктердің қалыпты таралымы.
Сол сияқты, кездейсоқ қателіктердің [х1 , х2] кескіндісіне түсу ықтималдығы, суреттегі штрихтелген фигураның ауданымен анықталады, яғни
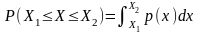
Систематикалық және кездейсоқ қателіктерді бағалау кезінде өлшеу нәтижелерінің математикалық күтімі деген ұғым қолданылады.
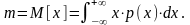
Систематикалық қателікті өлшенетін шаманың нақты мәні мен өлшеу нәтижелерінің математикалық күтімінің арасындағы ауытқу арқылы анықтауға болады.
Ө= М[Х]]- Хд
Ал кездейсоқ қателік - өлшеу нәтижесінің дара мәндері мен математикалық күтімінің арасындағы ауытқу арқылы сипатталады
δ = Х - М[Х]
Өлшеу нәтижелерінің математикалық күтім төңірегінде қаншалықты шашырап орындалуын сипаттайтын шама дисперсия.
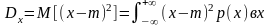
Және орта квадраттық ауытқу
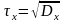
Егерде өлшеу нәтижелеріне систематикалық қателіктер енбеген жағдайда, кездейсоқшаманың математикалық күтімі өлшенетін шаманың нақты мәні болып табылады.
Өлшеу нәтижелерін бағалау нүктелік немесе интервалдық тәсілдермен іске асады. Мысалы, өлшеу нәтижелерінің сандары N – ге тең болсын, Х: х1, х2 ……..хN . Бағаланатын параметрлерге математикалық күтім мен орта квадраттық ауытқу жатады. Оценка а – параметрінің бағалануы а0 нүктелік болып табылады, егерде ол тек қана бір цифрмен айқындалса. Математикалық күтімнің m және дисперсияның Дх нүктелік бағалануы келесі формулалармен анықталады.


Интервалдық бағалау кезінде, өлшенетін шаманың нақты мәнін қамтитындай интервал табылады. Бұл интервалды сенімділік интервалы (доверительный интервал) дейміз.
Өлшенетін шаманың сенімділік интервалында жату ықтималдығын, сенімділік ықтималдылығы (доверительная вероятность) деп атайды. Мысалға, кездейсоқ шаманың таралымы қалыпты заңға бағынсын, дисперсияға Дх=δХ2. Бұл жағдайда математикалық күтімнің m (m-δх0;m+δх0) интервалына түсу ықтималдығы келесі өрнектен анықталады

Мұндағы
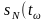 )–
Стьюдент таралымы, δх0
–
таңдамалы таралымының орта квадраттық
ауытқуы, m0
–
таңдамалы таралымының математикалық
күтімі,;
)–
Стьюдент таралымы, δх0
–
таңдамалы таралымының орта квадраттық
ауытқуы, m0
–
таңдамалы таралымының математикалық
күтімі,;

Егер сенімділік ықтималдылығы р және n=N-1 мәні белгілі болса, онда Стьюдент таралымының кестесінен tа - шамасын табамыз. Бұл жерде
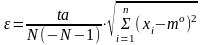
Таңдамалы таралымның дисперсия үшін (орта квадраттық ауытқу δх) сенімділік интервалы келесі қатынастан анықталады.
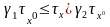
Мұндағы
 және
және
 Пирсон таралымынан (Х2
- таралымы) табылатын шамалар ( әдейіленген
кесте көмегімен).
Пирсон таралымынан (Х2
- таралымы) табылатын шамалар ( әдейіленген
кесте көмегімен).
Интервалдық
бағалау қайталап өлшеу сандары шектелген
жағдайда (N<30) қолданылады. Егерде
тәжірибе саны жеткілікті болған
жағдайда(N>30) Стьюдент таралымы қалыпты
таралымға айналады, бұл жағдайда
 және
,
шамаларын анықтаудың қажеті болмай
қалады.
және
,
шамаларын анықтаудың қажеті болмай
қалады.
Өлшеу құралдарының қателіктерін қосу.
Өлшеу құралдарының қорытқы қателігі, құрал құрамына кіретін элементтер қателіктерінің қосындысымен айқындалады, сол себептен қателіктерді қосу белгілі бір ереже бойынша орындалуы қажет. Қосу барысында систематикалық және кездейсоқ қателіктер өз алдына, мультипликативтік және аддитивтік қателіктер өз алдына қосылады.
Систематикалық қателіктер келесі формула арқылы қосылады.
 =
= 1
1 1
+
2
2
+
…
.n
n
1
+
2
2
+
…
.n
n
Мұндағы - салыстырмалық қателіктерді қосу үшін, олардың таралым заңдылықтарының қосындысын айқындау қажет. Бұл мәселе кездейсоқ қателіктер саны 3-4 тен асып кетсе өте қиын шешіледі. Сондықтан, есептеуді жеңілдету үшін кездейсоқ қателіктердің өзара байланыс дәрежелерін анықтайды және де кездейсоқ қателіктерді аддитивті және мультипликативті құрамдарға бөлу қажет. Аддитивті және мультипликативті қателіктер жеке- жеке қосылады. Кездейсоқ қателіктің қорытқы мәні (қосындысы) келесі формуламен анықталады.

мұндағы
 - кездейсоқ шамалардың арасындағы өзара
байланысты сипаттаушы, корреляция
коэффициенті. Егерде С=1 болса, онда
δΣ
– мәні алгебралық жолмен, ал С=0 болса,
геометриялық жолмен табылады.
- кездейсоқ шамалардың арасындағы өзара
байланысты сипаттаушы, корреляция
коэффициенті. Егерде С=1 болса, онда
δΣ
– мәні алгебралық жолмен, ал С=0 болса,
геометриялық жолмен табылады.
Есептеу
кездерінде егер Сkj>0,7,
болса, онда Сk
j
мәнін 1-ге теңеп алады да,
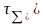 мәнін алгебралық жолмен табады. Егер
C
мәнін алгебралық жолмен табады. Егер
C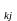 <
0.7 ,болса, онда Сk
j
= 0 деп қабылдап, қателік қосындысын
геометриялық жолмен табады.
<
0.7 ,болса, онда Сk
j
= 0 деп қабылдап, қателік қосындысын
геометриялық жолмен табады.
Есептеулерді жеңілдету үшін, мәндері аз мөлшерде болып келетін қателіктерді еспке алмайды. Мысалға, екі қателікті қосуды қарастырайық.
=
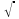
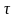
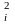 +
, мұндағы
1
>
2.
+
, мұндағы
1
>
2.
Егерде
2
< 0.05
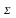 шарты орындалса, онда
шарты орындалса, онда
 қателігін
ескермесе де болады, яғни
қателігін
ескермесе де болады, яғни
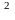 -
1
=
2.
Соңғы теңдеуден келесі теңсіздікті
алуға болады
-
1
=
2.
Соңғы теңдеуден келесі теңсіздікті
алуға болады
 ;
ары қарай
=
1
деп
ұйғарып алатынымыз
;
ары қарай
=
1
деп
ұйғарып алатынымыз

Сонымен, егер бір қателіктің мәні екіншісінен үш есе кем болса, онда ол қателікті ескермеуге болады. Бұдан шығатын салдар, үлгі аспабының өлшеу қателігі жұмыс аспабының өлшеу қателігінен кем дегенде үш есе кем болуы қажет.
Сонымен, қателіктерді қосу ережесін келесі түрде тұжырымдауға болады.
а) қателіктерді систематикалық және кездейсоқ аддитивті және мультипликативті қателіктерге жіктеу. Кездейсоқ қателіктер үшін математикалық күтім орта квадраттық ауытқу және таралым заңдылығын анықтау қажет, соннымен қатар қателіктердің өзара корреляциялық байланысын табу керек.
б) өлшеу құрылғысының систематикалық қателіктерінің қосындысын табу.
в) өлшеу құрылғысы үшін кездейсоқ қателіктерді қосу қажет. Ол үшін кездейсоқ қателіктердің математикалық күтімдерін өзара қосады, алынған қосындыға систематикалық қателікті қосады. Табылған қателікті қателіктің систематикалық бөлігі деп қарастырамыз. Кездейсоқ қателіктердің орта квадраттық ауытқуын және таралым заңдылығын анықтайды.
г) өлшеу құрылғысы қателігінің ∆х берілген сенімділік ықтималдылығы бойынша сенімділік интервалының шекаралық мәндерін келесі теңсіздіктен табу қажет.
М [∆x]-kδ(∆x)<∆x+М [∆x]+kδ(∆x)
Мұндағы М [∆x], δ(∆x) – берілген шамалар, k – қорытқы таралу заңдылығына және сенімділік ықтималдылығының мәніне тәуелді анықталатын коэффициент. Мысалға, егер таралым заңдылығы қалыпты болса, ал сенімділік ықтималдылығы р(-∆хг<х<∆хг)=0,95 тең болса, онда к=2.
2-дәріс бойынша тест сұрақтары
1.
Өлшеу қателігі келесі
өрнекпен анықталады δ= 100%
мұндағы Х–
абсолютті қателік, Х- өлшенетін шаманың
шынайы мәні. Қателіктің түрін анықта.
100%
мұндағы Х–
абсолютті қателік, Х- өлшенетін шаманың
шынайы мәні. Қателіктің түрін анықта.
+А) қатысты
В) келтірілген қатысты
С) абсолютті
D) статикалық
Е) динамикалық
2.
Өлшеу қателігі келесі өрнекпен анықталады
δП=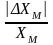 100%
мұндағы
ХМ
– абсолютті қателіктің максимал мәні,
ХМ –
өлшеу аспабының шкаласының максимал
мәні. Қателіктің түрін анықта.
100%
мұндағы
ХМ
– абсолютті қателіктің максимал мәні,
ХМ –
өлшеу аспабының шкаласының максимал
мәні. Қателіктің түрін анықта.
А) қатысты
+В) келтірілген қатысты
С) абсолютті
D) статикалық
Е) динамикалық
3. Егер өлшеу нәтижесінің ортаквадраттық ауытқуы х белгілі болса, дисперсия Д Х келесі өрнекпен анқыталады.
А) Д Х= ln(х )
В)

С) Д Х= Sin(х )
+D) (ДХ)=х2
Е) Д Х= 1/х
4. Өлшеу құрылғысының дәлділік класын анықтайтын сан аз болған сайын
А) жіберілетін қателіктің шегі үлкен болады
+В) жіберілетін қателіктің шегі аз болады
С) жіберілетін қателіктің дәлділік класынан тәуелсіз болады
D) жіберілетін қателіктің шегі аз болмайды
Е) жоғарыдағы барлық жауап дұрыс
5. Өлшеу қателігі деп өлшеу нәтижесінің неден ауытқуын айтамыз?
А) нөлден
В) өлшенетін шаманың максимал мәннен
С) өлшенетін шаманың минимал мәннен
D) шексіздіктен
+Е) өлшенетін шаманың шынайы мәннен
3-ДӘРІС
ӨЛШЕУ ҚҰРАЛДАРЫНЫҢ СТАТИКАЛЫҚ ЖӘНЕ ДИНАМИКАЛЫҚ СИПАТТАМАЛАРЫ
Өлшеу құралдарының статикалық сипаттамалары деп, тұрақталған режимдегі шығыстық хвых және кірістік хВХ шамалардың арасындағы функционалдық тәуелділікті айтады
|
(3.1) |
3.1 тәуелділігінде
|
(3.2) |
Статикалық сипаттамалар кесте, график және теңдеулер түрінде берілуі мүмкін.
Көп
жағдайда кірістік шама хВХ
шығыстық
шамаға
хВЫХ
тікелей түрленбейді, түрлендіру үшін
аралық түрленгіштер қолданылады. 3.1 –
суретте тізбектей жалғанған n-буыннан
тұратын өлшеу құралының құрылымдық
схемасы келтірілген. Мұндағы
 -
кірістік шама,
-
кірістік шама,
 - шығыстық шама, индекс 0 – тұрақталған
режимді білдіреді, ал қалған индекстер
буындардың реттік номерлеріне сәйкес
келеді. Кез-келген буынның статикалық
сипаттамасын келесі түрде жазуға болады.
- шығыстық шама, индекс 0 – тұрақталған
режимді білдіреді, ал қалған индекстер
буындардың реттік номерлеріне сәйкес
келеді. Кез-келген буынның статикалық
сипаттамасын келесі түрде жазуға болады.
|
n – ші буынның шығыстық шамасы
-
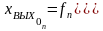
(3.3)
(3.3) – теңдеу буындары тізбектей жалғанған өлшеу құралының статикалық сипаттамасы болып табылады.
Е
 3.2
–сурет. Сызықты буынның статикалық
сипаттамасы
3.2
–сурет. Сызықты буынның статикалық
сипаттамасы
|
(3.4) |

3.3- сурет. Релелі буындардың статикалық сипаттамалары
мұндағы К – беріліс коэффициенті
Беріліс коэффициенті К тұрақталған режимдегі шығыстық шаманың кірістік шамаға қатынасымен анықталады.
Беріліс коэффициенті өлшеу аспаптарының, түрлендіргіштердің, датчиктердің сезімталдығын сипаттайды. Бейсызықты элементтер және аспаптар үшін, сезімталдылық статикалық және дифференциалдық болып бөлінеді.
Статикалық сезімталдылық
|
(3.5) |
Дифференциалдық сезімталдылық
|
(3.6) |
Сызықты элементтер және өлшеу құралдары үшін
|
(3.7) |
Өлшеу құралының сезімталдығы, құралдың құрамына кіретін буындардың сезімталдығымен анықталады. Құрамына тізбектей жалғанған буындар кіретін өлшеу құралының сезімталдығы былайша анықталады:
|
(3.8) |
Буындар өзара паралеллель жалғанған жағдайда (3.4 - сурет) келесі қатынас тура
|
(3.9) |
Буындар
қарсы-параллель жалғанған жағдайда
(3.5
- сурет),
1-элементтің шығыстық шамасы 2-ші
элементтің кірісіне беріледі, ал 2-ші
элементтің шығыстық сигналы
( )
1-ші
элементтің кірісіне беріледі. Егерде
2-ші элементтің шығыстық сигналы 1-ші
элементтің кірістік сигналымен қосылса,
онда оң кері байланыс деп, егер ол
сигналдар бір-бірінен алынып тасталса,
онда теріс кері байланыс деп аталады.
)
1-ші
элементтің кірісіне беріледі. Егерде
2-ші элементтің шығыстық сигналы 1-ші
элементтің кірістік сигналымен қосылса,
онда оң кері байланыс деп, егер ол
сигналдар бір-бірінен алынып тасталса,
онда теріс кері байланыс деп аталады.


3.4 сурет Параллель жалғау 3.5 сурет Қарсы-параллель жалғау
Әдетте өлшеу құралдарында теріс кері байланыс кеңінен қолданылады. Егерде теріс кері байланыс орын алған жағдайда (3.5-сурет) келесі қатынас тура
|
(3.10) |
Егер кері байланыс байланыс оң болса, онда
|
(3.11) |
Жалпы жағдайда, тура тізбекте n элемент кері тізбекте бірнеше элементтер орналасса, онда
|
(3.12) |
мұндағы Ki – тура тізбектегі элементтің коэффициенттері, КОС – кері тізбектегі элементтің коэффициенттері
Өлшеу құралдарының динамикалық сипаттамасы деп, өтпелі процесс кезіндегі шығыстық хВЫХ және кірістік хВХ шамалардың арасындағы функционалдық тәуелділікті айтады.
Динамикалық сипаттамалар толық және дербес болып бөлінеді. Толық динамикалық сипаттамаларға жататыны: дифференциалдық теңдеу, импульстік сипаттама h(t), өтпелі сипаттама h1(t), беріліс функциясы K(р), амплитудалық-жиіліктік А () және фазалық-жиіліктік () сипаттамалардың жиынтығы.
Дербес динамикалық сипаттамаларға жататындары: толық динамикалық сипаттамалардың кейбір параметрлері, мысалға уақыт тұрақтысы, кешігу уақыты, шығыс сигналының тұрақталу уақыты т.с.с. әдетте бұл сипаттамалар нормалданады.
Динамикалық сипаттамаларды тәжірибе жүзінде де алуға болады. Импульстік сипаттаманы алу үшін, өлшеу құралының кірісіне бірлік импульс беріліп, шығыстық шамасының h(t) өзгеріс заңдылығы тіркеледі.
Өтпелі сипаттаманы алу үшін өлшеу құралының кірісіне бірлік секіртпелі ықпал беріліп, шығыстық шамасы h1(t) тіркеленеді.
Өлшеу тәсілдеріне қарай өлшеу аспаптары келесі түрлерге бөлінеді: тұйықталмаған структуралық схемасы, салыстыру тәсіліне негізделген аспаптар (3.6, а - сурет); тұйықталған структуралық схемасы, теңгеру тәсіліне негізделген аспаптар (3.6, б - сурет) және аралас (комбинированные) аспаптар.
С

3.6-сурет. Аспаптардың құрылымдық схемасы:
а – тұйықталмаған; б - тұйықталған; ИМ- өлшеу механизмі; РУ – тіркеуіш құрал; УС-салыстырмалы құрал; УН – қателікті күшейту құралы; УМ — қуатты күшейткіш; ОП — кері түрлендіргіш; УП-басқарылатын түрлендіргіш.
алыстыру аспаптарында бастап шығыстық шамадан X бастап шығыстық шамаға Y дейін барлық түрлендірулер бір бағытта жүреді, яғни кірістен шығысқа қарай. Түрлендіру нәтижесінде X шамасы кванттауға, кодтауға және жадыда сақтауға ыңғайлы түрде Y – шамасына түрленіп шығады.
Теңгеру тәсіліне негізделген аспаптарда, теңгеру процессін іске асыру үшін салыстыру элементінде Х = X - Хк айырымы түзіледі. Цифрлық аспаптарда басқарылатын түрлендіргіштің (УП) шығыстық шамасы код болып келеді.
Теңгеру тәсіліне негізделген автоматты өлшеу аспаптарының динамикалық қасиетін талдау үшін беріліс функциясы қолданылады.
Тұйықталған автоматты өлшеу аспабының құрылымдық схемасындағы тура тізбекте бір буын болған жағдайдағы беріліс функциясы
|
(3.13) |
Тура тізбекте үш буын орналасқан жағдайдағы беріліс функциясы
=
 /
(1 +
/
(1 +

Егерде төмендегі қатынастарды еске алсақ

және Хк(р) ==Х(р)-Х(р), онда теңгерілмеген шаманың кескіні мынаған тең:
|
(3.14) |
Сонымен
қатар, құрылымдық схемаға кіретін
интегралдаушы буын санына да тәуелді
болып келеді. Бұл тәуелділікті талдау
үшін тұрақталған режимдегі X=const;
 және
және
 шығыстық шаманың Y(t) теңгерілмеген
шамаға X
тәуелділігін қарастырайық.
шығыстық шаманың Y(t) теңгерілмеген
шамаға X
тәуелділігін қарастырайық.
Шығыстық шаманың кескіні
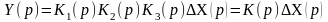
Тура тізбекте интегралдаушы буын болған жағдайда, беріліс функциясы мынаған тең
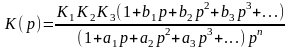

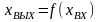
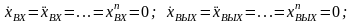
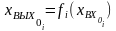
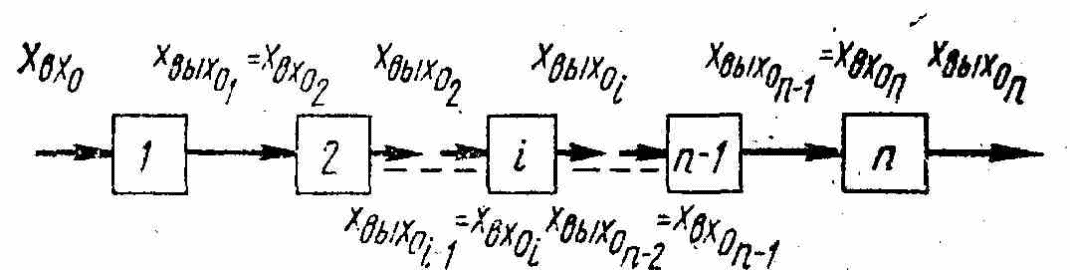 3.1
– сурет. Буындары тізбектей жалғанған
өлшеу құралының структуралық
схемасы
3.1
– сурет. Буындары тізбектей жалғанған
өлшеу құралының структуралық
схемасы