3.Нормальный закон распределения
Нормальный закон распределения (часто называемый законом Гаусса) имеет широкий круг приложений и занимает среди других законов распределения особое положение. Основная особенность, выделяющая нормальный закон среди других, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся условиях.
Уравнение для плотности нормального распределения имеет вид:
(8.4)
что соответствует функции в Excel НОРМРАСП при соответствующем значении параметра интегральная.
Рис.8.2.Интегральная и дифференциальная функции распределения для нормального закона
Вообще данная функция имеет следующий синтаксис: НОРМРАСП (х; среднее; стандартное отклонение; интегральная).
Весьма важной практической задачей является определение вероятности того, что случайная величина попадет на заданный интервал вещественной оси (а, b). Для нормального распределения она определяется следующей формулой:
(8.5)
На практике часто встречается задача, обратная задаче вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно математического ожидания х. Формула для вероятности попадания случайной величины на участок, симметричный относительно математического ожидания, имеет следующий вид:
(8.6)
где l — половина длины участка, симметричного относительно математического ожидания.
В решении этой задачи может помочь функция Excel НОРМОБР. Вообще, функция обратного нормального распределения (НОРМОБР) используется в ситуациях, когда известна вероятность определенного значения случайной величины и необходимо рассчитать это значение. Синтаксис: НОРМОБР (вероятность; среднее; стандартное отклонение).
В качестве границ интервалов часто берутся точки, отстоящие от математического ожидания на целое число стандартных отклонений (обычно σ, 2σ, Зσ). Приведем значения вероятности попадания нормально распределенной величины в интервалы с такими границами.
Таблица 8.1
Границы интервала |
Вероятность |
-σ, +σ |
0,68269 |
-2σ, +2σ |
0,95450 |
- Зσ, +Зσ |
0,99730 |
4.Пример выполнения лабораторной работы
Задание
Для закупки и последующей продажи мужских курток фирмой было проведено исследование мужского населения города в возрасте от 18 до 65 лет в целях определения его среднего роста. В результате было установлено, что средний рост 176см, стандартное отклонение 6см. Рост мужского населения города распределен по нормальному закону.
Необходимо:
1.Построить нормальный закон распределения с заданными параметрами.
2.Определить, какой процент общего числа закупаемых курток должны составлять куртки 5-го роста (182—186см).
3.Рассчитать границы интервала роста мужского населения города, вероятность попадания в который случайной величины роста составляет 0,95.
Сгенерируем совокупность случайных величин, подчинённых нормальному закону распределения с заданными математическим ожиданием - 176 и среднеквадратическим отклонением - 6, воспользовавшись средством «Анализ данных» – «Генерация случайных чисел» MS Excel. Диалоговое окно заполним следующим образом (рис. 8.3.).
Далее построим для сгенерированного ряда значений интегральную и дифференциальную функции распределения, воспользовавшись мастером диаграмм MS Ecxel (рис 8.4.), вычислив предварительно значения этих функций на сгенерированном множестве случайных чисел с помощью функции НОРМРАСП, и произведя сортировку с помощью команды «Данные» - «Сортировка» по значениям сгенерированной случайной величины.
Рис.8.3.Генерация случайных чисел, подчинённых нормальному закону распределения с математическим ожиданием – 176 и среднеквадратическим отклонением – 6.
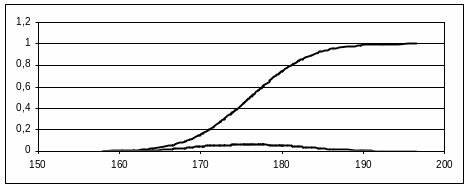
Рис.8.4.Нормальный закон распределения с математическим ожиданием – 176 и среднеквадратическим отклонением – 6
Для определения процента общего числа закупаемых курток 5-го роста (182—186см) необходимо найти вероятность попадания случайной величины в заданный интервал, то есть вычислить НОРМРАСП(186;176;6;ИСТИНА) и НОРМРАСП(182;176;6;ИСТИНА), а также взять разность полученных вероятностей:
= 0,95221 - 0,84134 = 0,11086 (8.7).
Таким образом, куртки 5-го роста должны составлять приблизительно 11% общего числа закупаемых курток.
Для определения границы интервала роста мужского населения города, вероятность попадания в который случайной величины роста составляет 0,95 предварительно необходимо преобразовать аргументы НОРМОБР к стандартному виду, в результате чего имеем
l = НОРМОБР ((P + 1)/2;0; σ) (8.8).
После подстановки данных получим формулу
= НОРМОБР ((0,95 + 1)/2;0;6) (8.9),
которая рассчитает значение 11,7598. Таким образом, границы искомого интервала составят математическое ожидание минус/плюс полученное значение отклонения 164,24 и 187,76 см.