Лабораторная работа 50 Бинарные деревья
Цель работы: изучить создание и работу с бинарными деревьями, научиться решать задачи с использованием бинарных деревьев на языке C++.
Теоретические сведения
Бинарное (двоичное) дерево – это динамическая структура данных, состоящая из элементов, каждый из которых содержит информационное поле и не более двух ссылок на различные бинарные поддеревья. На каждый элемент дерева имеется ровно одна ссылка. Каждая вершина бинарного дерева является структурой, состоящей из четырех видов полей. Содержимым этих полей будут, соответственно:
информационное поле (ключ вершины);
служебное поле (их может быть несколько или ни одного);
указатель на левое поддерево;
указатель на правое поддерево.
Начальный узел называется корнем дерева, ему соответствует нулевой уровень. Узел, не имеющий поддеревьев, называется листом. Исходящие узлы называются предками, входящие – потомками. Для каждого предка выделяют левого и правого потомка. Уровень потомка на единицу превосходит уровень его предка. Высота дерева определяется количеством уровней, на которых располагаются его узлы.
На рисунке схематично представлена структура бинарного дерева, у которого все узлы до 3 уровня имеют по два потомка, а все узлы уровня 3 являются листами.
Рис. Бинарное дерево
Список можно представить как частный случай бинарного дерева:
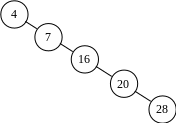
Рис. Список как частный случай бинарного дерева
Структура дерева отражается во входном потоке данных так: каждой вводимой пустой связи соответствует условный символ, например, '*' (звездочка). При этом сначала описываются левые потомки, затем, правые. Для структуры бинарного дерева, представленного на следующем рисунке, входной поток имеет вид: ABD*G***CE**FH**J**.
Рис. Адресация в бинарном дереве
Описание бинарного дерева выглядит следующим образом:
struct имя_типа {
информационное поле;
[служебное поле;]
адрес левого поддерева;
адрес правого поддерева;
};
где информационное поле – это поле любого ранее объявленного или стандартного типа;
адрес левого (правого) поддерева – это указатель на объект того же типа, что и определяемая структура, в него записывается адрес следующего элемента левого (правого) поддерева.
Например:
struct point {
int data;//информационное поле
int count; //служебное поле
point *left;//адрес левого поддерева
point *right;//адрес правого поддерева
};
Если дерево организовано таким образом, что для каждого узла все ключи его левого поддерева меньше ключа этого узла, а все ключи его правого поддерева – больше, оно называется деревом поиска. Одинаковые ключи не допускаются. В дереве поиска можно найти элемент по ключу, двигаясь от корня и переходя на левое или правое поддерево в зависимости от значения ключа в каждом узле. Такой поиск гораздо эффективнее поиска по списку, поскольку время поиска определяется высотой дерева, а она пропорциональна двоичному логарифму количества узлов. Для списка среднее время поиска равно половине длины списка. В идеально сбалансированном дереве количество узлов справа и слева отличается не более чем на единицу.
Деревья и списки являются рекурсивными структурами, т.к. каждое поддерево также является деревом. Таким образом, дерево можно определить как рекурсивную структуру, в которой каждый элемент является:
либо пустой структурой;
либо элементом, с которым связано конечное число поддеревьев.
Действия с рекурсивными структурами удобнее всего описываются с помощью рекурсивных алгоритмов.
Обход дерева
Для того, чтобы выполнить определенную операцию над всеми узлами дерева, все узлы надо обойти. Такая задача называется обходом дерева. При обходе узлы должны посещаться в определенном порядке. Существуют три принципа упорядочивания. Рассмотрим бинарное дерево. На нем можно определить три метода упорядочивания:
Слева направо: Левое поддерево – Корень – Правое поддерево;
Сверху вниз: Корень – Левое поддерево – Правое поддерево;
Снизу вверх: Левое поддерево – Правое поддерево – Корень.
Эти три метода можно сформулировать в виде рекурсивных алгоритмов.
void Run(point*p) { //обход слева направо
if(p) {
<обработка p->data>
Run(p->left);//переход к левому поддереву
Run(p->right);//переход к правому поддереву
}
}
Если в качестве операции обработки узла поставить операцию вывода информационного поля, то получим функцию для печати дерева.
Формирование дерева поиска
Пример 1. Формируется и выводится на экран дерево поиска. Указываются уровни узлов.
#include <iostream.h>
#include <stdlib.h>
struct Point {//описание структуры бинарного дерева
int number; //информационное поле
Point* left; //указатель на левое поддерево
Point* right; //указатель на правое поддерево
};
Point* Add(Point*root,int d); //построение дерева поиска
void Out(Point* p,int n); //печать дерева
void main() {
int k;
cout<<"k= ";
cin>>k;
Point* p=new Point;
p->number=k;
p->left=0;
p->right=0;
do {
cout<<"k= ";
cin>>k;
Add(p,k);
}
while(k!=0);
Out(p,0);
}
Point* Add(Point*root,int d) {
//добавление элемента d в дерево поиска
Point*p=root;//корень дерева
Point*r;
//флаг для проверки существования элемента d в дереве
int ok=0;
while(p&&!ok){
r=p;
if(d==p->number)ok=1;//элемент уже существует
else
if(d<p->number)p=p->left;//пойти в левое поддерево
else p=p->right;//пойти в правое поддерево
}
if(ok) return p;//найдено, не добавляем
//создаем узел
Point* New_point=new Point();//выделили память
New_point->number=d;
New_point->left=0;
New_point->right=0;
//если d<r->key, то добавляем его в левое поддерево
if(d<r->number)r->left=New_point;
//если d>r->key, то добавляем его в правое поддерево
else r->right =New_point;
return New_point;
}
void Out(Point* p, int n) {//Печать бинарного дерева
//*p - указатель на корень дерева.
cout <<"\nУровень "<<n<<": ";
cout<<p->number<<' ';
n++;
if(p->left!=NULL) Out(p->left,n);
if(p->right!=NULL) Out(p->right,n);
}
Пример 2. Формируется и выводится на экран идеально сбалансированное дерево.
#include <iostream.h>
#include <stdlib.h>
struct Point {//описание структуры бинарного дерева
int number; //информационное поле
Point* left; //указатель на левое поддерево
Point* right; //указатель на правое поддерево
};
Point* Tree(int n, Point* p);
//построение идеально сбалансированного дерева
void Out(Point* p,int n); //печать дерева
void main(){
int k;
cout<<"Число узлов дерева: k= ";
cin>>k;
Point* p=new Point;
delete p;
p->left=0;
p->right=0;
Tree(k, p);
Out(p,0);
}
//построение идеально сбалансированного дерева
Point* Tree(int n,Point* p) {
Point*r;
int nl,nr;
if(n==0){
p=NULL;
return p;
}
nl=n/2;
nr=n-nl-1;
r=new Point;
cout<<"?";
cin>>r->number;
r->left=Tree(nl,r->left);
r->right=Tree(nr,r->right);
p=r;
return p;
}
//печать бинарного дерева
void Out(Point* p, int n) {
// *p - указатель на корень дерева
cout <<"\nУровень "<<n<<": ";
cout<<p->number<<' ';
n++;
if(p->left!=NULL) Out(p->left,n);
if(p->right!=NULL) Out(p->right,n);
}
Перед компиляцией кода в среде MSVC++ необходимо в меню Options/Project отключить режим Use Microsoft Foundation Classes.
Задания
Наберите код программы из Примера 1. Выполните компиляцию и запуск программы.
Найдите количество четных элементов дерева поиска. Укажите эти элементы и их уровни.
Домашние задания
Наберите код программы из Примера 2. Выполните компиляцию и запуск программы.
Найдите сумму элементов идеально сбалансированного дерева, находящихся на уровне k.