Нагадаємо, що ресурси j та і називаються взаємозамінювальними, якщо і та взаємодоповнювальними, якщо і
Висновок 7) випливає з даного означення та висновку 5).
Зауважимо, що у випадку конкретних виробничих функцій зроблені вище висновки випливають з конкретного аналітичного вигляду розв’язків (8.5). Для детального вивчення даної теми варто скористатись літературою [13,19].
Завдання №9 Тема: „Неокласична довгострокова модель багато продуктової фірми в умовах досконалої конкуренції”
Нехай
фірма є багато продуктовим виробником,
тобто виробляє вектор продуктів
,
використовуючи при цьому вектор
виробничих ресурсів
.
Вважаючи, що нам відомі вектор цін на
продукцію
,
вектор цін на ресурси
та функціональна модель технологічних
зв’язків між векторами у і х, тобто
векторна виробнича функція:
,
(9.1)
де
довгострокову модель багато продуктової
фірми в умовах досконалої конкуренції
(відомі ціни
і
фірма не намагається вплинути на них)
можна записати у вигляді наступної
задачі математичного програмування:
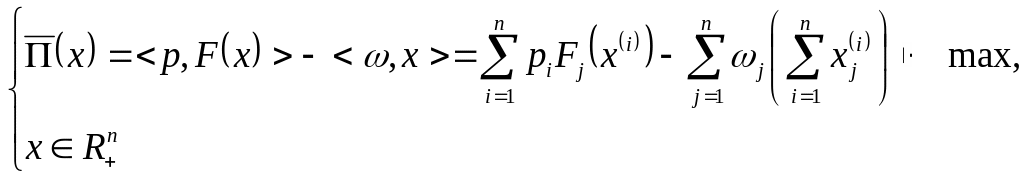(9.2)
У випадку неокласичної виробничої функції (9.1) є задача (9.2) є задачею угнутого програмування. Крім того, за своїм змістом задача (9.2) збігається із задачею (9.1).
1. На основі моделі (9.2) у випадку двох продуктового виробництва, що використовує два види ресурсів, зв’язок між якими описується векторною виробничого функцією
(9.3)
знайти
при заданих додатних значеннях
функції попиту на ресурси
(9.4)
та функції пропозиції продукції
(9.5)
Дослідити властивості цих функцій.
2.
Обчислити значення попиту на виробничі
ресурси та пропозиції продукції в точках
якщо:
а)
б)
Результати оформити у вигляді окремих таблиць.
Допоміжний теоретичний матеріал. Необхідні умови екстремуму для неокласичної задачі (9.2) мають вигляд [13,19]:
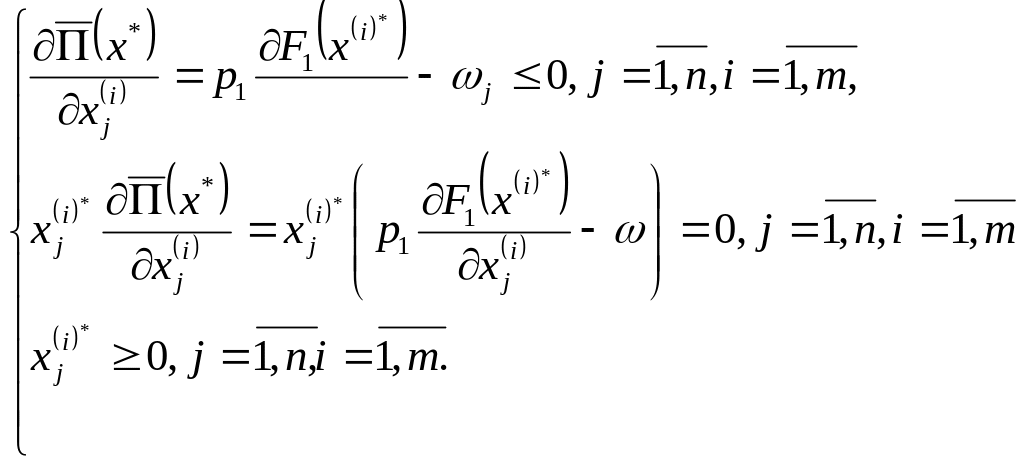(9.6)
Зробивши
змістовне припущення про те, що всі
виробничі фактори використовуються
для виробництва всіх видів продукції
(тобто що
),
від умов (.6) прийдемо до необхідних умов
(9.7)
Розв’язавши співвідношення (9.7) у випадку n=m=2 та векторної виробничої функції (9.3) одержимо функції попиту на ресурси (9.4) і функції пропозиції продукції (9.5). Подальше дослідження цих функцій і якісний аналіз на основі цих функцій здійснюється аналогічно до того, як це було зроблено у випадку одно продуктової моделі.
Знаходження конкретних числових значень попиту і пропозиції є елементарною задачею.
Варіанти вихідних даних для завдання №9 подані у таблицях 4 і 4.1
Варіант |
|
|
|
1 |
20 |
30 |
0.1 |
2 |
50 |
60 |
0.3 |
3 |
80 |
70 |
0.2 |
4 |
90 |
10 |
0.1 |
5 |
100 |
50 |
0.8 |
6 |
10 |
10 |
0.3 |
7 |
40 |
50 |
0.4 |
8 |
80 |
80 |
0.1 |
9 |
100 |
150 |
0.8 |
10 |
110 |
120 |
0.15 |
11 |
10 |
30 |
0.45 |
12 |
100 |
20 |
0.77 |
13 |
50 |
30 |
0.31 |
14 |
30 |
70 |
0.44 |
15 |
120 |
200 |
0.17 |
16 |
80 |
160 |
0.71 |
17 |
130 |
140 |
0.66 |
18 |
110 |
50 |
0.29 |
19 |
30 |
90 |
0.47 |
20 |
100 |
100 |
0.12 |
Таблиця 4.1
Варіант |
|
|
|
1 |
0.8 |
0.9 |
0.05 |
2 |
0.2 |
0.4 |
0.5 |
3 |
0.2 |
0.3 |
0.3 |
4 |
0.7 |
0.5 |
0.2 |
5 |
0.1 |
0.6 |
0.6 |
6 |
0.3 |
0.3 |
0.3 |
7 |
0.5 |
0.5 |
0.4 |
8 |
0.1 |
0.4 |
0.4 |
9 |
0.15 |
0.2 |
0.35 |
10 |
0.16 |
0.17 |
0.18 |
11 |
0.35 |
0.5 |
0.45 |
12 |
0.2 |
0.88 |
0.1 |
13 |
0.44 |
0.52 |
0.17 |
14 |
0.33 |
0.88 |
0.11 |
15 |
0.19 |
0.31 |
0.37 |
16 |
0.12 |
0.9 |
0.06 |
17 |
0.1 |
0.77 |
0.2 |
18 |
0.35 |
0.57 |
0.13 |
19 |
0.27 |
0.5 |
0.38 |
20 |
0.19 |
0.39 |
0.42 |
Завдання 10
Завдання 11