Завдання №7 Тема: „Еколого-економічні функції структурного типу та їх побудова”

Проблеми забруднення довкілля набули на сьогоднішнії день особливої актуальності [9]. В першу чергу це зв’язано з динамікою сучасної світової економіки, яка характеризується збільшенням об’ємів природних ресурсів, задіяних у виробничій діяльності, а також в багатоьх вупадках неконтрольованими об’ємами різноманітних виробничих відходів, що викидаються у навколишнє середовище. Зрозуміло, що обійтись без формалізованих (зокрема, математичних) досліджень вгалузі еколого-економічної взаємодії тут не можна, оскільки абстрагування від реальних економічних або еколого-економічних систем і процесів до їх математичних моделей і, навпаки, перехід від якісного аналізу цих моделей до висновків про динаміку реальних економічних чи еколого-економічних систем і процесів – один з найбільш ефективних і економічних методів вивчення подібних проблем.

Серед задач еколого-економічного моделювання важливе значення мають задачі побудови математичних моделей еколого-економічних функцій – функцій, які дають можливість оцінити корисність досліджувального еколого-економічного процесу та визначити тенденцію його розвитку. Еколого-економічні функції як і виробничі функції (в їх класичному розумінні) мають не лише самостійне значення, але й виступають в ролі окремих підмоделей більш складних еколого-економічних процесів і систем [2].

Розглянемо одну із задач еколого-економічного менеджменту – задачу оптимальної організації виробництва з урахуванням узагальнення класичної задачі оптимального планування на дві групи виробництв: основного виробництва (матеріального виробництва) і допоміжного виробництва (знищення продуктів забруднення) [10].

Нехай - вектор валової (основної) продукції, - вектор знищених забруднювачів (допоміжної продукції), - квадратна матриця затрат продукції i на випуск одиниці j, - прямокутна матриця затрат продукції i на знищення одиниці забруднювачів l, - прямокутна матриця випуску забруднювачів l під час випуску одиниці продукції j, - квадратна матриця випуску забруднювачів l при знищенні одиниці забруднювачів s, - вектор максимально можливих об’ємів наявних виробничих ресурсів, - вектор мінімального допустимих об’ємів знищених забруднювачів при функціонуванні даних виробничих технологій. Матриці A,B,C,D складаються з невід’ємних елементів. Оскільки сумарні затрати на виробництво основної продукції і знищення забруднювачів не можуть перевищувати наявних виробничих ресурсів, а сумарне вироблене забруднення є не меншим від знищеного, то Au + Bv <=x, Cu + Dv >=z. Якщо - питомі оцінки відповідно основної і допоміжної продукції (наприклад, р – питомий дохід, а q – питомі затрати), то мету виробництва можна формалізувати у вигляді задачі

(7.1)

де

Вважаючи A,B,C,D,p,q заданими, а x,z – параметрами, дійдемо висновку, що задача лінійного програмування (7.1) задає неявно функцію

(7.2)

яка кожній парі ставить у відповідність невід’ємне значення де - розв’язок задачі (7.1) при заданих x,z. Функція (7.2) визначена в області ø . Потрібно:

1. Дослідити властивості еколого-економічної функції (7.2).

2. При n=2, m=1, 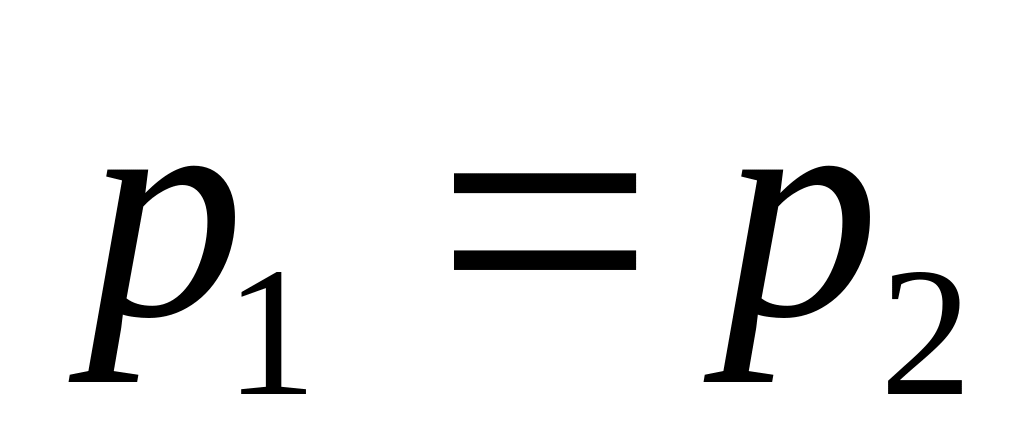=5, q=2 і заданих A,B,C,D побудувати функцію (7.2) у явному аналітичному вигляді.

Допоміжний теоретичний матеріал. Функція (7.2) в рбласті О є угнутою, неперервною у всіх внутрішніх точках, монотонно неспадною по компонентам вектора z, додатно однорідною першого степеня і в загальному випадку кусково-лінійною. Побудову функції (7.2) можна здійснити, користуючись методикою, описаною у завданні 6. Випишемо двоїсту до (7.1) задачі:

(7.3)

де . Оскільки в задачі (7.3) множина не залежить від параметрів x i z, то ми можемо знайти всі опорні розв’язки системи лінійних алгебраїчних рівнянь

(7.4)

де - вектори допоміжних змінних (передбачається, що матриця системи(7.4) не має жодного базисного вектора стовпця ). Виконуючи алгоритм, описаний раніше, прийдемо до функції

де - підобласті лінійності функції (7.5), - сукупність допустимих вершин множини . Таким чином, функція (7.2) набуде вигляду (7.5).

Розглянемо приклад. Нехай

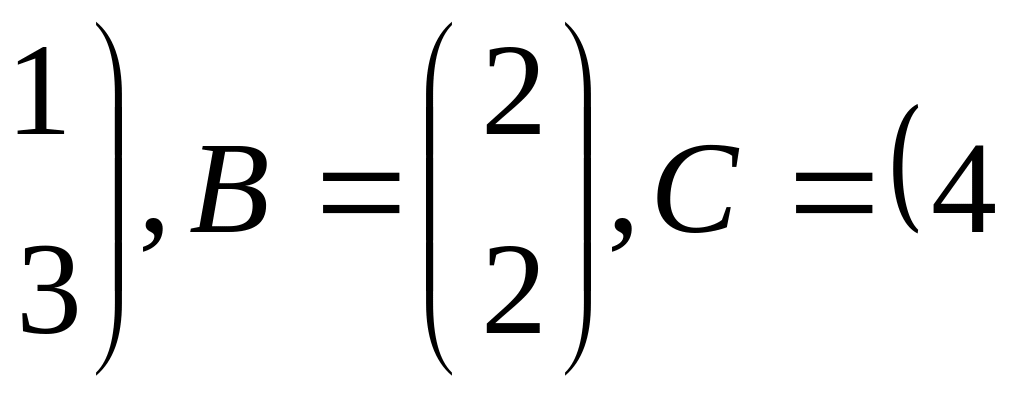
Тоді

Варіанти вихідних даних для завдвння №7 (Матрицю А взяти із завдання №6)

1) (3 3), C = (1 2), D = 4

2) (4 5), C = (2 2), D = 1

3) (1 3), C = (1 2), D = 5

4) (7 3), C = (5 4), D = 2

5) (8 9), C = (1 3), D = 4

6) (3 4), C = (7 7), D = 10

7) (11 9), C = (8 8), D = 9

8) (9 10), C = (1 1), D = 3

9) (12 5), C = (2 5), D = 2

10) (10 20), C = (7 8), D = 7

11) (15 10), C = (1 4), D = 4

12) (17 19), C = (15 15), D = 12

13) (14 9), C = (11 11), D = 8

14) (4 11), C = (1 5), D = 3

15) (4 11), C = (3 3), D = 13

16) (20 20), C = (7 3), D = 1

17) (9 9), C = (2 8), D = 4

18) (3 13), C = (4 14), D = 9

19) (2 12), C = (3 10), D = 5

20) (10 10), C = (1 2), D = 7.