Завдання№5

Тема: ”Основні типи виробничих функцій”

До найбільш поширених типів виробничих функцій, що використовуються як на мікро – так і на мікрорівні, належать уже відома нам степенева функція (функція Кобба - Дугласа)

(5.1)

виробнича функція із сталою еластичністю заміщення (CES-функція, назва якої походить від англійського терміну constant elasticity of substitution )

(5.2)

виробнича функція з постійними пропорціями (виробнича функція Леонтьєва)

(5.3)

лінійна виробнича функція

(5.4)

Всі параметри функцій (5.1)-(5.4) є додатними.

CES-функцію можна розглядати як певне узагальнення функцій

1. а) Переконатись в тому, що для функції (5.2) виконується всі неокласичні гіпотези.

б) Виписати формули для числових характеристик

в) Показати, що при та деяких обмеженнях на параметри функція (5.2) збігається до функції (5.1), а числові характеристики CES- функції збігаються до відповідних характеристик функції Кобба-Дугласа.

2. а) Дослідити властивості функції (5.3), зокрема при n=2.

б)Показати, що при та певних обмеженнях на c, b, CES-функції(5.2) збігається до функції з постійними пропорціями (5.3).

в) Користуючись результатами попередніх досліджень, визначити

2. а) Переконатися в тому, що при 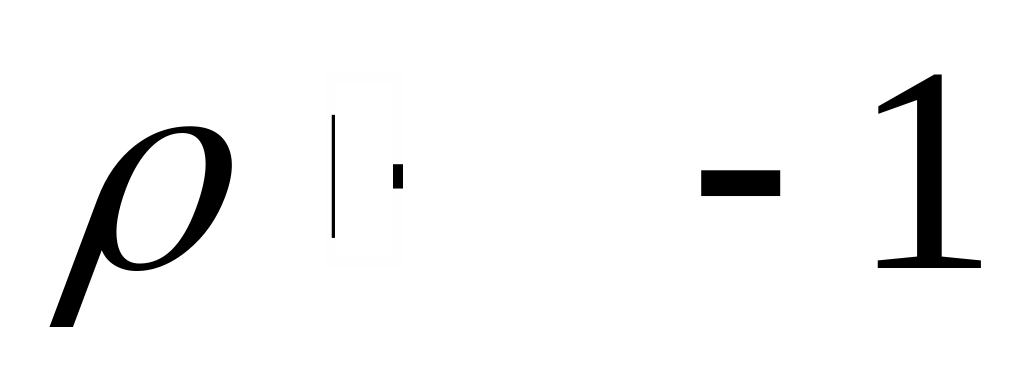і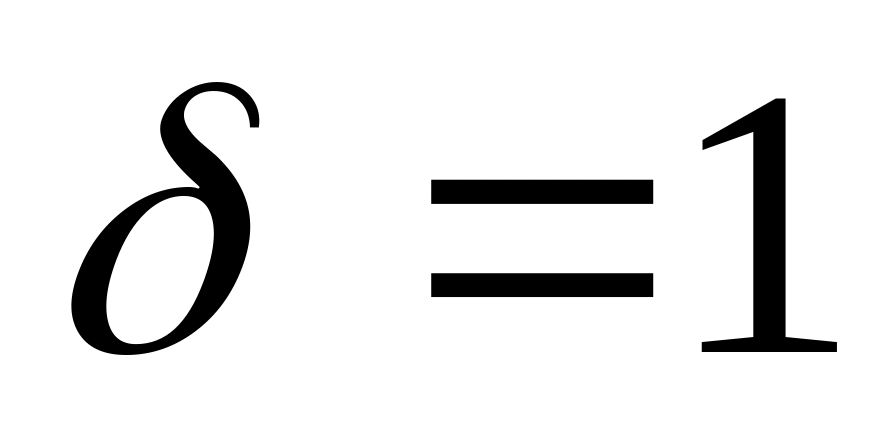 CES-функція (5.2) збігається до лінійної виробничої функції (5.4)

б) Визначити основні характеристики виробничої функції (5.4).

в) Побудувати функцію (5.4) при n=2 на основі числових даних таблиці 3

Допоміжний теоретичний матеріал. Спочатку знайдемо числові характеристики функції (5.1) і переконаємось, що

Зауважимо, що еластичність виробництва характеризує віддачу від розширення масштабів виробництва. Ця віддача буде зростаючою, постійною або спадаючою, якщо відповідно

або . CES-функція належить до функцій, які є близькими до степеневих, але відрізняються обмеженими можливостями заміщення ресурсів (для функції Кобба- Дугласа вони є необмеженими, тобто не реальними, що пояснюється поведінкою ізокванти – лінії рівня). Еластичність заміщення функції є постійною, але відмінною від одиниці. Для того, щоб зробити граничні переходи від функції (5.2) до функції (5.1) зручно від (5.2) перейти до еквіваленту форми

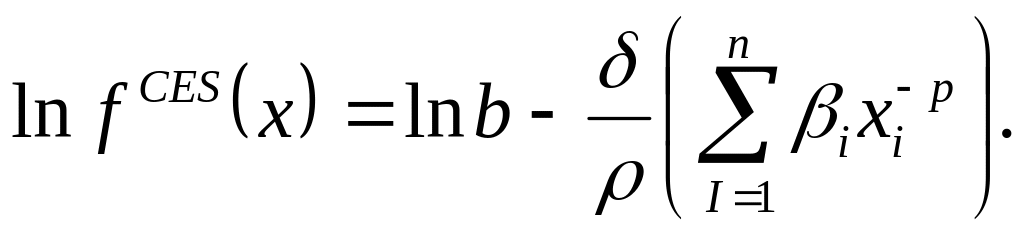(5.5)

Користуючись (5.2) і (5.5) потрібно показати що

1) якщо b = a, ;

2) якщо ;

3) якщо

4)

5)

Перейшовши в (5.5) до границі при і застосувавши правило Лопіталя, одержимо

де Останнє співвідношення означає, що тобто якщо c=b, Оскільки за означенням еластичності виробництва (функції)

(5.6)

то .

Формула також проводить до цього результату, оскільки серед доданків є тільки одна одиниця, а інші рівні нулю. Цей фактор легко обґрунтувати, зокрема при n=2. Можливість заміщення одного ресурсу іншим тут повністю відсутня, тому функція і називається функцією з постійними пропорціями. Про граничну норму заміщення, як правило , не говорять, а обмежуються тільки еластичністю заміщення ресурсів

Що стосується лінійної виробничої функції, то вона одержується в результаті граничного переходу від CES- функції при Справді,

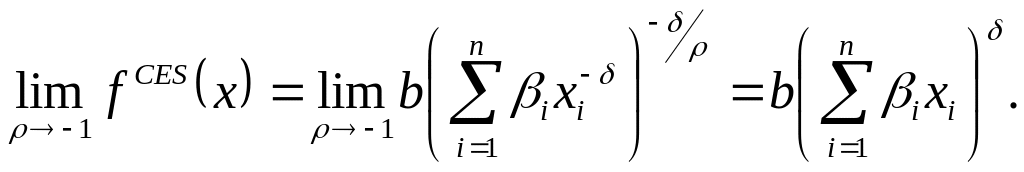Всі характеристики лінійної виробничої функції легко знаходяться за формулами (4.4) - (4.8). Зазначимо лише, що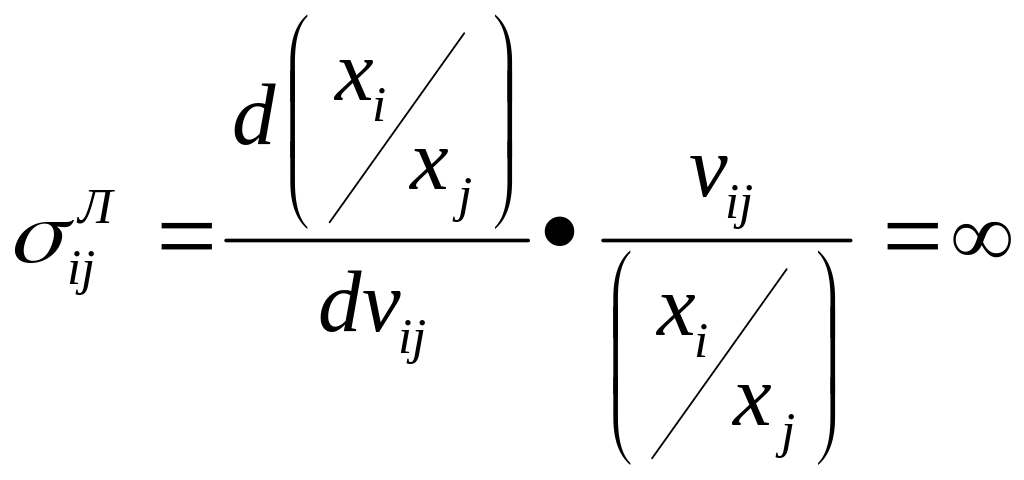 , оскільки гранична норма заміщення ресурсів є постійною (вона не залежить від співвідношення задіяних у виробництві ресурсів), тобто 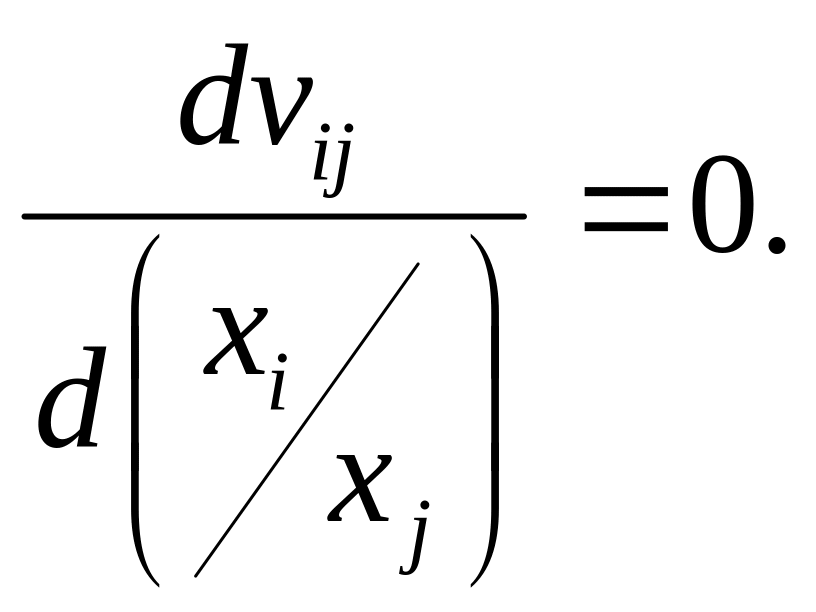Крім того,

Якщо позначити , то при A=0 функція (5.4) збігається з функцією (4.2). Відкинемо у системі (4.3) перший стовпчик і перший рядок, після цього отримаємо систему нормальних рівнянь для визначення параметрів де

Кожний з типів виробничих функцій має свою область застосування Степеневі виробничі функції (або функції Кобба - Дугласа) частіше всього використовується для моделювання середньомасштабних економічних систем (від виробничого об’єднання до галузі), які характеризуються стійким функціонуванням (кожна одиниця використаного ресурсу дає ефект, пропорційний середній продуктивності (ефективності)даного ресурсу). CES- функція застосовується в тих випадках, коли немає точної інформації про рівень взаємного заміщення виробничих ресурсів, але відомо, що цей рівень суттєво не зміниться при зміні об’ємів виробничих ресурсів, тобто є близьким до сталої величини. При наявності засобів ідентифікації параметрів CES-функція може використовуватись для моделювання економічних систем різного рівня. Виробнича функція з постійними пропорціями (функція Леонтьєва) використовується для моделювання строго детермінованих технологій, які зустрічаються, як правило, в дрібномаштабних або повністю автоматизованих виробничих процесах. Цікавим є той факт, що функцію Леонтьєва можна отримати як розв’язок задачі математичного програмування

Лінійна виробнича функція використовується для моделювання крупно масштабних систем (велика галузь, народне господарство в цілому), в яких продукція, що випускається, є результатом одночасного функціонування багатьох різних тенологій.

Для детального вивчення теорії виробничих функцій корисними будуть літературні джерела [2,11-14,19].