Завдання №1

Тема: „Моделі поведінки споживачів”

Нехай поведінка споживача визначається неокласичною функцією корисності , доходом I та вектором цін на товари p = , де A>0, >0, >0, p >0, <1, I>0, T-символ операції транспортування.

1.Користуючись моделлю раціональної (оптимальної) поведінки споживача, визначити бажаний набір товарів x та максимальне значення функції корисності при заданих

2.Побудувати функцію попиту споживача x = , x та функцію граничної вартості грошей = використовуючи графічний метод розв’язування задач нелінійного програмування

3.Побудувати функції x та , використовуючи умови оптимальності розв’язку задачі угнутого програмування (умови Куна-Таккера)

4.Виписати рівняння Слуцького для кожного з товарів та, скориставшись уже відомою функцією попиту споживача x визначити матрицю Слуцького при довільних p, I та при p= Уточнити властивості цієї матриці.

5 .При заданих та відповідному цим величинам оптимальному наборі товарів і оптимальному значенні граничної вартості грошей , обчислити матрицю Слуцького, користуючись тільки функцією корисності.

6. Здійснити класифікацію товарів і визначити граничну норму заміщення одного товару іншим.

7. За допомогою коефіцієнтів еластичності визначити чутливість попиту на кожний з товарів відносно цін та доходу при і переконатись тому, що для кожного товару сума всіх еластичностей за цінами і доходами є нульовою.

8. Перевірити виконання умов агрегації Ангеля і Курно та переконатись в тому, що всі товари з кошика споживача одночасно не можуть бути малоцінними, а значення попиту на j – го товару, в якій ваговими коефіцієнтами є ціни товарів.

Допоміжний теоретичний матеріал. Модель раціональної поведінки споживача формалізується у вигляді так званої неокласичної задачі споживання:

де - невід’ємний ортант n- вимірного векторного простору, <,>- операція скалярного добутку, u(x) – строго угнута (опукла в гору) функція корисності від набору товарів х.

При n = 2 розв’язування задачі (1.1) графічним методом зводиться до розв’язування системи рівнянь

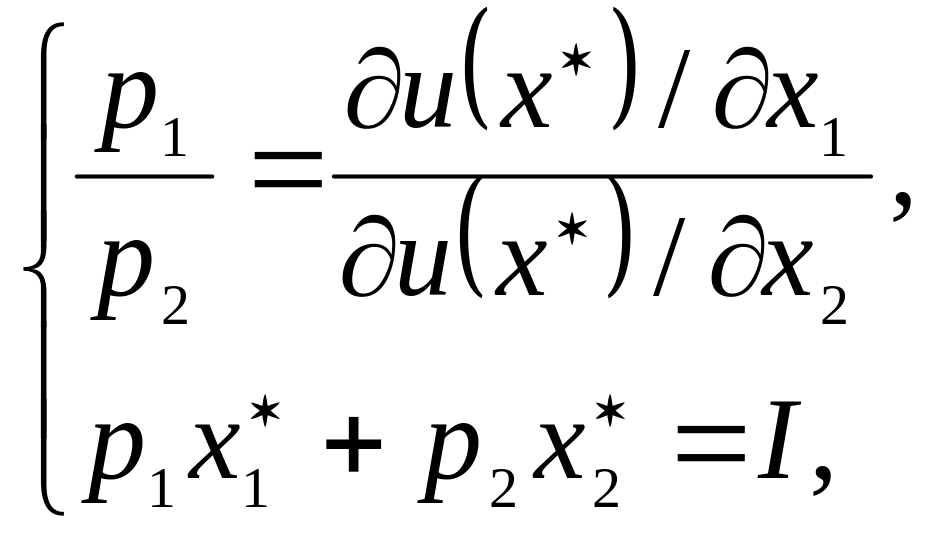
(1.2)

де - шуканий розв’язок . У загальному випадку змістовний розв’язок задачі (1.1) визначається умовами оптимальності Куна – Танкера для регулярної задачі угнутого (опуклого) програмування, тобто умовами

(1.3)

де - оптимальне значення двоїстої змінної. Оскільки у рамках даного завдання простір товарів є двохвимірним, то функції попиту споживача можна побудувати двома способами. Перший конкретизується системою (1.2), а другий – системою (1.3).

Рівняння Слуцького у векторній формі для товару j записується так:

(1.4)

де зміна попиту при зміні ціни j-го товару, - зміна попиту при зміні ціни j-го товару з компенсацією доходу, - зміна попиту при зміні доходу. З рівнянь (1. 4) можна визначити матрицю Слуцького

С =

При конкретних p = І = матриця С є числовою матрицею, при чому вона буде симетричною, від’ємно напіввизначеною, а с_jj < 0, j= . Матрицю Слуцького можна обчислити також за формулою:

С= , (1.5)

Де >0, H= - матриця Гессе.

При заданих та можна обчислити, користуючись формулою (1.5) зауважимо, що під добутком матриці – стовпця S на матрицю – рядок R розуміється матриця:

SR= .

Товар j називається цінним, якщо >0 та малоцінним, якщо . Крім того, товар j буде нормальним, якщо та товаром Гіффена, якщо . Гранична норма заміщення товару l товаром j визначається за формулою:

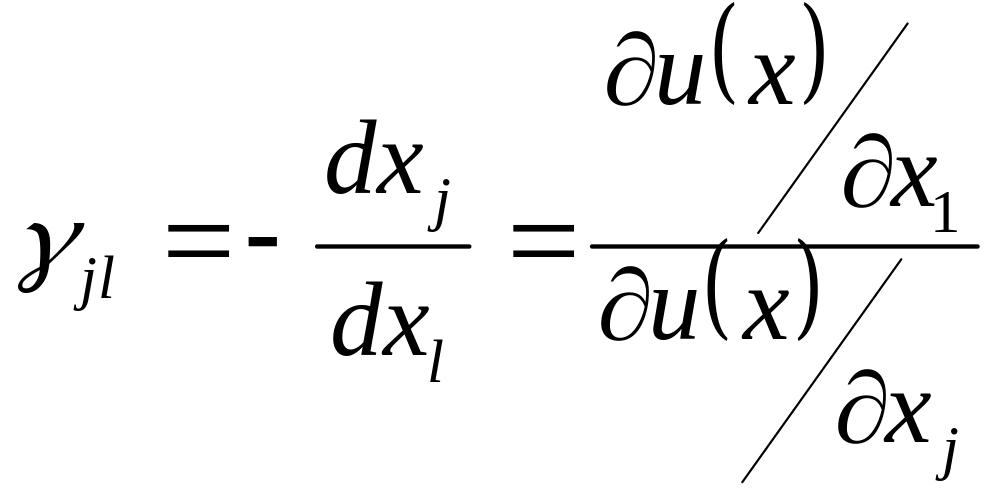(1.6)

Формула (1.6) показує, скільки одиниць товару j потрібно, щоб замінити вибувши малу одиницю товару l.

Товари l та j називаються взаємозамінювальними, якщо 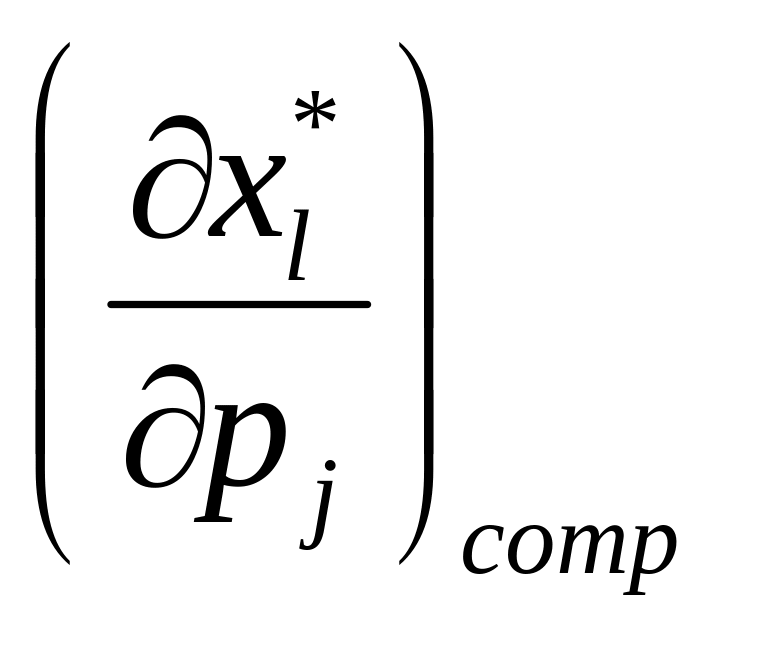>0 та взаємодоповнювальними, якщо 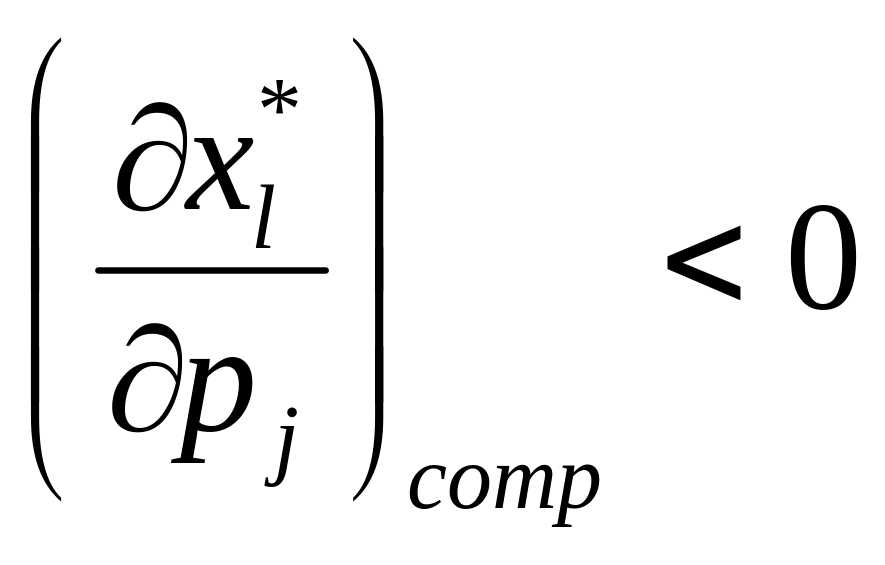. У випадку двох товарів вони завжди є взаємозамінювальними.

Як відомо, характеристикою чутливості зміни залежної змінної від змін незалежної змінної замість похідної у економіці використовують коефіцієнти еластичності. Чутливість попиту на кожний з товарів відносно цін та доходу при заданих визначається за допомогою відповідних коефіцієнтів еластичності:

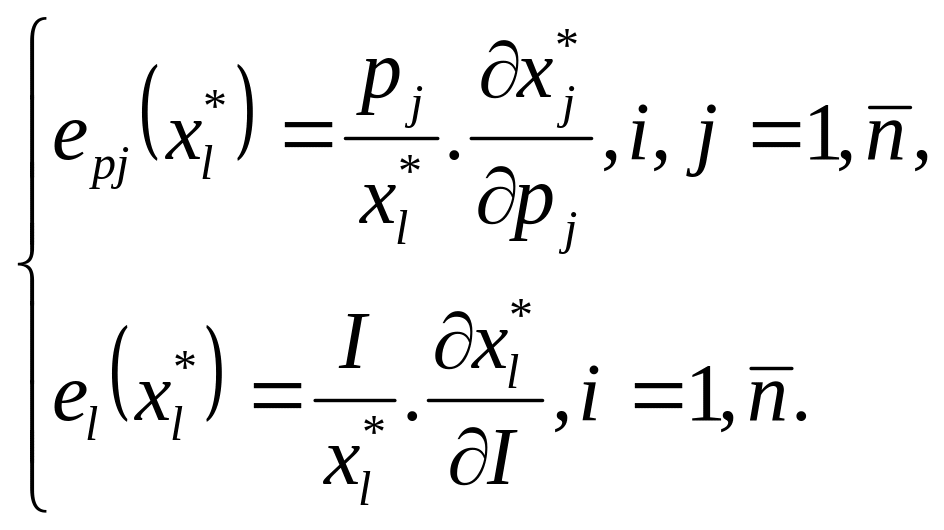(1.7).

Умова агрегації Ангеля у матрично-векторній формі має вигляд: або . У розгорнутій формі ця умова записується так:

Умова агрегації Курно у матрично-векторній формі задається співвідношенням:

,

де 0=(0,...,0), 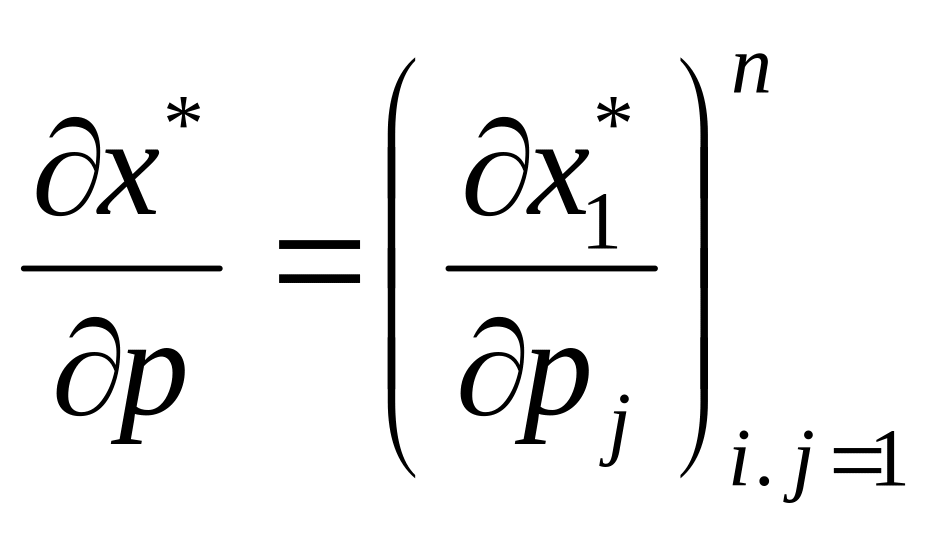, а у розгорнутій формі –

Для виконання завдання 1 та поглибленого вивчення неокласичної моделі споживання рекомендується опрацювати главу 1[2, ч. ІІ, с. 120-131], главу 1 [19, ч. І, с. 9-40], главу 1 [13, ч. ІІ, с. 91-102].

Варіанти вихідних даних для завдання №1 подані у таблицях 1 і 1.1.

Таблиця 1

Варіанти
1	5	1/2	1/4
2	6	1/3	2/9
3	7	3/7	1/2
4	10	5/8	1/4
5	11	7/11	3/11
6	8	1/7	5/7
7	9	3/5	1/5
8	15	4/9	4/9
9	13	1/8	5/8
10	14	3/10	1/10
11	20	1/4	1/4
12	18	1/9	2/3
13	19	7/9	1/9
14	25	1/3	1/3
15	30	3/7	3/7
16	27	1/6	1/6
17	28	3/8	1/2
18	16	1/6	1/2
19	17	1/7	1/7
20	12	2/9	2/9

Таблиця 1.1

Варіанти
1	3	4	100
2	6	7	90
3	10	5	80
4	8	9	70
5	2	1	60
6	5	7	110
7	8	3	120
8	4	5	130
9	1	2	150
10	11	12	200
11	9	9	190
12	2	4	180
13	4	8	190
14	8	16	180
15	3	9	170
16	2	6	160
17	1	7	100
18	4	10	200
19	5	9	150

Завдання №2

Тема: „ Моделі поведінки споживачів та їх застосування”.

1. Використовуючи неокласичну задачу споживання, формалізувати у вигляді окремої математичної моделі проблему вибору між заробітком та дозвіллям (вільним часом) споживача, припускаючи, що дозвілля d (вільний час у годинах) є одним з товарів, а дохід споживача І складається з нетрудового доходу N і трудового доходу T=rt, t – робочий час у годинах, r – рівень заробітної платні за одну годину, q = d + t – загальний наявний час у годинах. Параметрами будемо вважати N, r, q та вектор цін на товари p (N 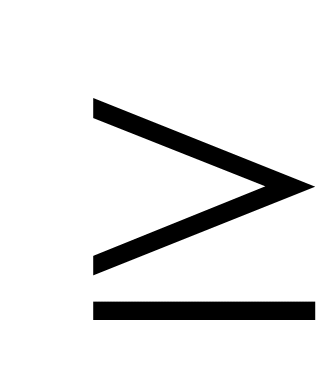0, r>0, q>0, p>0), а невідомими набір товарів і d. 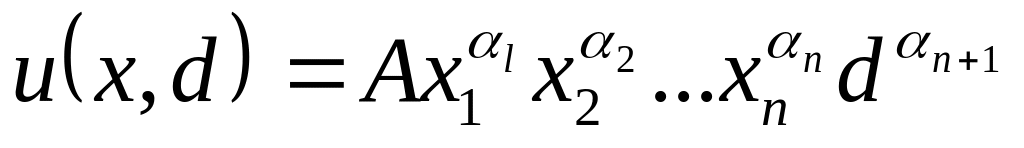У випадку неокласичної функції корисності 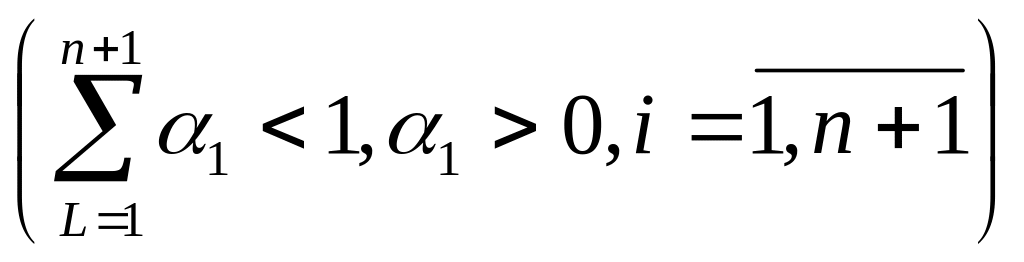- виписати умови оптимальності Куна – Танкера для 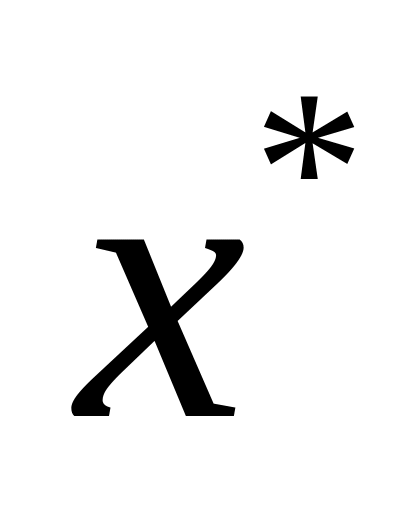і .

2. Скориставшись отриманими умовами оптимальності при n=2, А= 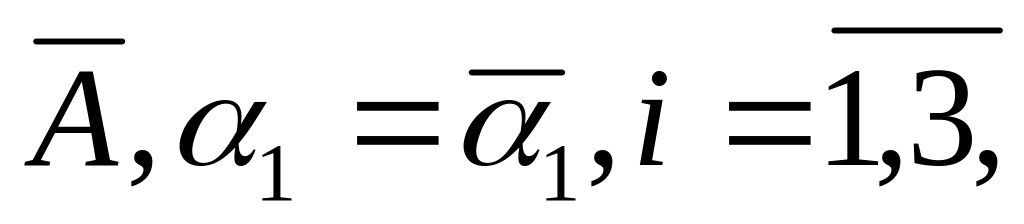побудувати функцію попиту споживача 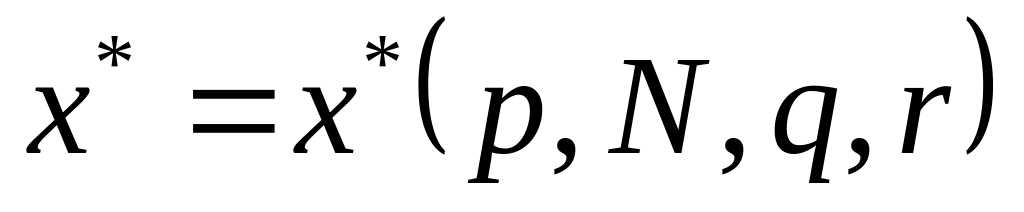(або 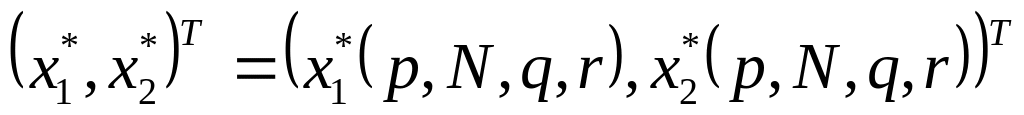) для товарів та функцію попиту для дозвілля 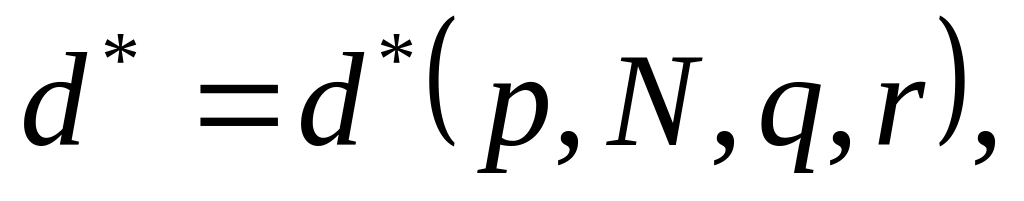а також функцію граничної вартості грошей . Встановити, чи є заробіток і вільний час взаємозамінювальними або взаємодоповнювальними.

3. Уточнити класифікацію кожного з товарів та з’ясувати чи може дозвілля бути малоцінним товаром або товаром Гіффена. Написати формули для коефіцієнтів еластичності попиту на кожний з товарів та дозвілля відносно параметрів

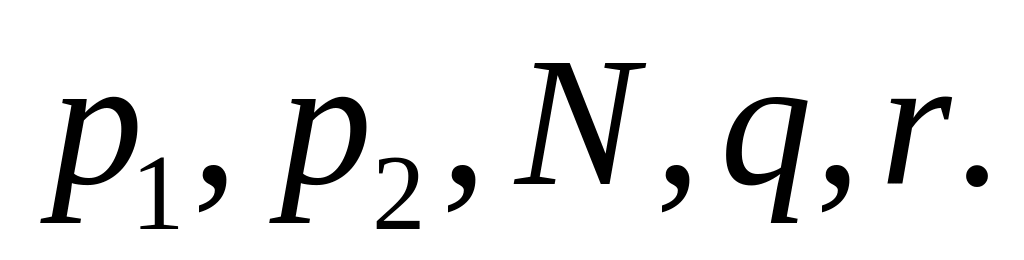
4. Визначити бажаний набір товарів та дозвілля.( 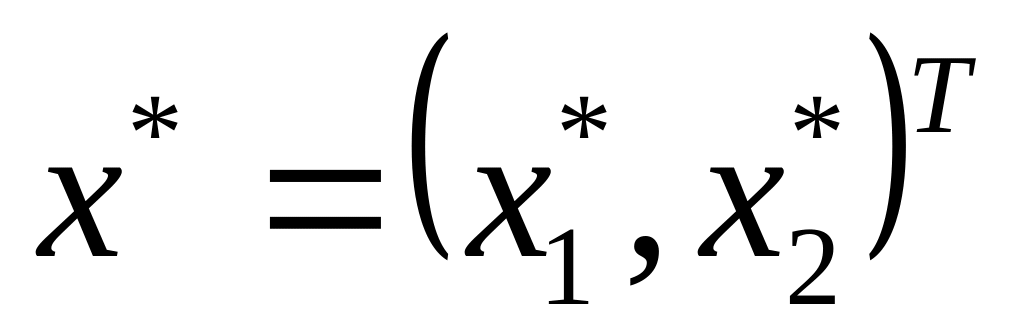та ), а також відповідне їм максимальне значення функції корисності при заданих

Допоміжний теоретичний матеріал. Враховуючи той факт, що I = N + rt, a t = q – d, тобто < p, x> N+r(q-d), проблему вибору між заробітком та дозвіллям формалізуємо у вигляді наступної задачі угнутого програмування:

(2.1)

Із (2.1) випливає, що ціною дозвілля як окремого товару (ціною однієї години дозвілля) є зарплатня за одну годину r. Конкретизувавши для задачі (2.1) відомо теорему Куна – Танкера, одержимо для і необхідні і достатні умови оптимальності, з яких для реальних , сформуємо систему рівнянь:

(2.2)

де - Оптимальне значення двоїстої змінної.

Для того, щоб побудувати функції у явному аналітичному вигляді, потрібно при розв’язати систему (2.2), залежну від параметрів p, N, r, q ( зокрема, при n=2).

Для дослідження того чи є заробіток і вільний час взаємозамінювальними або взаємодоповнювальними необхідно, користуючись рівняннями Слуцького для кожного з товарів, з’ясувати знаки похідних

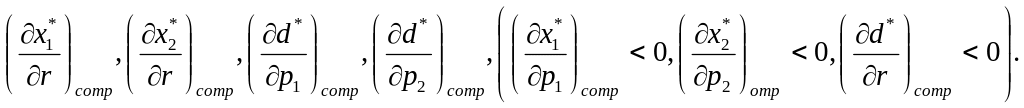
Якщо, наприклад, то це означає, що другий товар і дозвілля є взаємозамінювальними. В протилежному випадку вони будуть взаємодоповнювальними. Такий аналіз здійснюється для кожної пари, що складається з доповідного товару і вільного часу чи навпаки. Зауважимо лише, що у рівнянні Слуцького (1.4) замість змінних І, треба вживати відповідно змінні N,d^*,r.

Для класифікації кожного з товарів і дозвілля, зокрема, слід вияснити знаки похідних

Коефіцієнти еластичності визначаються згідно формул аналогічних до (1,7).

Бажаний набір товарів та дозвілля знайдено, обчисливши значення функцій попиту при Підставивши ці значення у функцію корисності, одержимо шукане максимальне значення цієї функції

.

Успішне виконання завдвння №2 також грунтується на засвоєнні теоритичного матеріалу, рекомендованого при підготовці завдання №1.

Варіанти вихідних даних для завдання №2 подані у таблицях 2 і 2,1.

Таблиця 2

Варіант
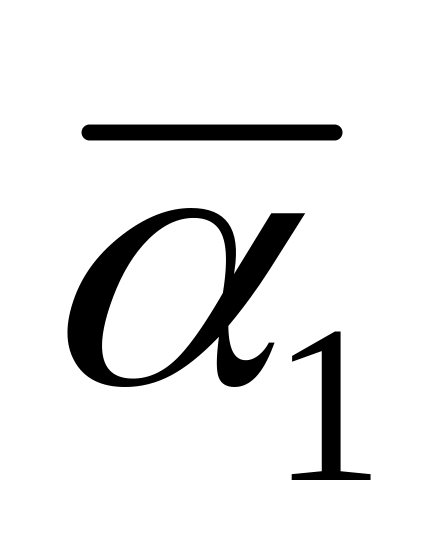
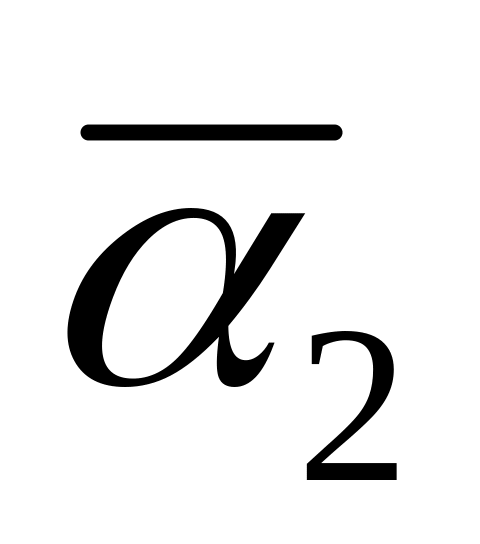
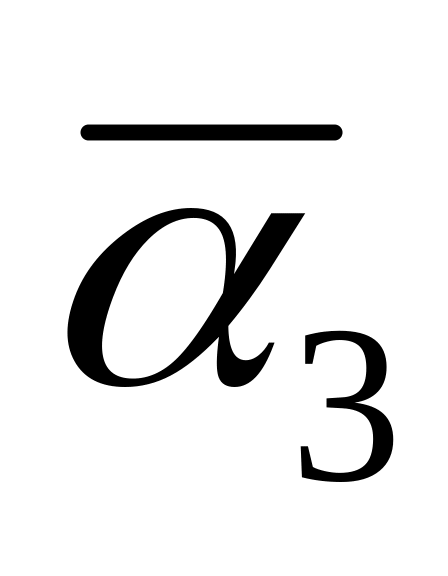
1	12	1/4	1/4	1/4
2	17	5/17	5/17	5/17
3	16	3/16	3/16	3/16
4	28	9/28	9/28	9/28
5	27	8/27	8/27	8/27
6	30	7/30	7/30	7/30
7	25	6/25	6/25	6/25
8	19	5/19	5/19	5/19
9	18	1/18	1/18	1/18
10	20	3/20	3/20	3/20
11	14	3/14	3/14	3/14
12	13	4/13	4/13	4/13
13	15	2/15	2/15	2/15
14	9	2/9	2/9	2/9
15	8	1/8	1/8	1/8
16	11	3/11	3/11	3/11
17	10	3/10	3/10	3/10
18	7	2/7	2/7	2/7
19	6	1/6	1/6	1/6
20	5	1/5	1/5	1/5

Таблиця 2.1

Варіант
1	1	7	40	20	4
2	4	10	45	21	5
3	5	9	50	22	6
4	2	6	55	23	7
5	3	9	60	24	8
6	8	16	65	20	4
7	9	9	70	21	5
8	2	4	75	22	6
9	4	8	80	23	7
10	11	12	85	24	8
11	1	2	90	20	4
12	7	7	95	21	5
13	4	5	100	22	6
14	8	3	95	23	7
15	5	7	90	24	8
16	2	1	85	20	4
17	8	9	80	21	5
18	10	5	75	22	6
19	3	4	70	23	7
20	6	7	65	24	8

Завдання №3