1.6. Способы построения перспективы

В настоящее время применяют различные способы построения перспективы пространственного геометрического объекта. Среди существующих способов наибольшее распространение получили радиальный способ и способ архитекторов. Оба эти способы основаны на построении перспектив по ортогональным проекциям объекта и широко используются в градостроительстве, при проектировании интерьера, в промышленном и ландшафтном дизайне.

Наглядные перспективные изображения можно также получить, используя способы перспективных масштабов, дистанционных точек, перспективной сетки, а также способ малой и большой картины.

1. Радиальный способ построения перспективы. Пусть требуется построить перспективу куба (рис.1.35). При радиальном способе построения перспективы куба с верхним и нижним ABCD основаниями точку S зрения и картинную плоскость Π_K задают в ортогональных проекциях.

Задаваясь расположением линии горизонта hh, находим по линии проекционной связи фронтальную проекцию S₂. Из точки S₁ к вершинам, ₁, A_{1,…, 1},D₁ куба проводим лучи зрения и определяем точки, _H, А_H,…, _H, D_H, пересечения их с плоскостью Π_K. Строим фронтальные проекции S₂ ,

S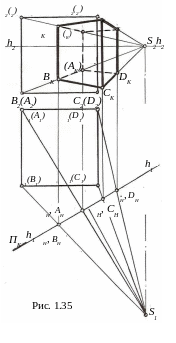 ₂A₂,…, S_{2 2}, S₂D₂ лучей зрения и, проведя из точек _H, А_H,…, _H,D_H линии проекционной связи, на соответствующих фронтальных проекциях лучей зрения находим перспективы _K, А_K,…, _K, D_K вершин куба. Соединяя последовательно найденные перспективы вершин прямыми линиями с учетом видимости, получаем перспективу куба.

Как видно из полученных построений, перспектива куба оказалась совмещенной с его фронтальной проекцией, что является определенным недостатком способа. Вместе с тем радиальный способ является простейшим при построении перспективы, не требует знания теории перспективы и предпочтителен при изображении объектов, горизонтальная проекция которых имеет много непараллельных между собой прямых линий.

Перспективу пространственного объекта можно построить без совмещения её с фронтальной проекцией. Так, задаваясь расположением фронтальной проекции линии горизонта hh, точкой S (S₁, S₂) зрения и ортогональными проекциями куба (рис.1.36), размещаем картинную плоскость П_К перпендикулярно П₁ вдоль оси y_13, . Из горизонтальной проекции S₁ к точкам , A₁,…, ₁,D₁ проводим горизонтальные проекции лучей зрения до пересечения с Π_K в точках _H, A_H,…, _H, D_H.

Из фронтальной проекции S₂ к точкам ₂, ₂,…, A₂, D₂,… проводим фронтальные проекции лучей зрения до пересечения с осью Z₂₃. Поворотом Π_K вокруг оси Z₂₃ до совмещения с плоскостью Π₃ и проведением из найденных точек пересечения линий проекционной связи, находим перспективы _K, _K, _K , _K и A_K, B_K, C_K и D_K вершин верхнего и нижнего оснований куба. Последовательно соединяя найденные перспективы вершин прямыми линиями с учётом видимости, получим перспективу куба.

2. Способ архитекторов. В основу способа положено свойство параллельных прямых в перспективе сходиться в одну точку. Рассмотрим данный способ на примере построения перспективы куба (рис.1.37).

Обозначим, как и ранее, точками , , , и A, B, C, D вершины верхнего и нижнего оснований куба (рис.1.37, а). Проведём картинную плоскость Π_K перпендикулярно горизонтальной плоскости Π₁ проекций через ребро B куба. Из точки S зрения проводим проекции лучей зрения к вершинам ₁, A,…, ₁,D до пересечения с плоскостью Π_K в точках _H, A_H,…, _H,D_H и лучи SF₁ и SF₂, соответственно параллельно сторонам , BC, , AD и , AB, , DC, где F₁ и F₂ – точки схода перспектив соответствующих пучков параллельных прямых. Так как эти линии горизонтальные, то точки схода F₁ и F₂ их перспектив будут располагаться на линии горизонта hh на расстоянии PF₁ и PF₂ от главной точки P картины.

Отметив на картинной плоскости Π_K линию горизонта hh, главную точку P картины и точки схода F₁ и F₂ перспектив параллельных прямых, приступаем к построению перспективы куба (рис.1.37,б). Боковое ребро B

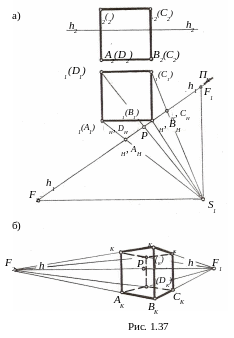
расположено вертикально в натуральную величину на картинной плоскости Π_K на расстоянии P _H≡PB_H от точки P картины. Точка B≡B_K расположена на основании OO картины, поскольку нижнее основание куба лежит на плоскости Π₁ проекций, которая выполняет роль предметной плоскости T. Точка ≡ _K расположена выше на расстоянии, равном B.

Найденные перспективы _K и B_K позволяют найти перспективы всех остальных вершин куба. Для этого, замеряя расстояния P _H=PA_H, P _H= PC_H и P _H=PD_H , отмечая на линии hh расположения боковых ребер A, C и D и, используя точки схода F₁ и F₂ параллельных рёбер куба, находим перспективы _K, A_K, _K, C_K и _K,D_K .Соединяя последовательно найденные перспективы вершин прямыми линиями с учётом видимости, получаем перспективу куба.

3. Способ перспективных масштабов. Сущность способа перспективных масштабов рассмотрим на примере построение перспективы куба. Пусть куб лежит на предметной плоскости T так, что две его грани A E и B C параллельны картиной плоскости Π_K (рис.1.38,а). Тогда рёбра AE, BC, и параллельны, а рёбра AB, CE, и перпендикулярны плоскости Π_K. Начальные точки 1_H, 2_H, 3_H и 4_H являются точками пересечения прямых 1, 2, 3 и 4, проведённых вдоль соответствующих рёбер, с плоскостью Π_K. Перспективы этих прямых проходят через начальные точки в главную точку P картины.

Если на картинной плоскости Π_K (рис.1.38,б) задана перспектива A_K вершины A нижнего основания ABCE, то при известной длине l ребра куба построение его перспективы можно выполнить в следующей последовательности:

1. Через точки A_K и P проводим перспективу прямой, проходящей вдоль ребра AB, до пересечения с основанием OO картины в точке1_H. Используем масштаб широт, на линии OO откладываем отрезок 1_H2_H, равный l.

2. Проводим перспективу 2_HP прямой, проходящей вдоль ребра CE.

3. Так как сторона AE нижнего основания куба параллельна плоскости Π_K, то её перспективу A_KE_K проводим параллельно основанию OO.

4. Отрезок прямой BE является диагональю квадрата ABCE и наклонён к плоскости Π_K под углом 45°. Перспектива прямой, проходящей вдоль диагонали BE, проходит через точкуE_K и дистанционную точку D. Точка B_K есть перспектива точки B.

Если точка D располагается вне пределов картинной плоскости Π_K, то можно воспользоваться дробной дистанционной точкой, например D/2. В этом случае отрезок A_KE_K точкой M_K, являющийся перспективой середины стороны AE, разделяем пополам и соединяем её прямой с точкой D/2. В точке пересечения этой прямой с перспективой 1_HP находим перспективу B_K.

Точка 5_H есть начальная точка прямой, проходящей вдоль диагонали BE. По масштабу глубин расстояние от точки B до картинной плоскости Π_K равно отрезку 1_H5_H.

5. Используем масштаб высот, от точек 1_H и 2_H вертикально вверх откладываем отрезки 1_H4_H и 2_H3_H. Далее проводим перспективы 4_HP и 3_HP прямых 4 и 3. Из вершинA_K, B_K, С_K и E_K перспективы нижнего основания проводим вертикальные прямые до пересечения с перспективами 4_HP и 3_HP получаем перспективы _K, _K, _K и _K вершин верхнего основания.

6. Последовательно соединяя найденные перспективы вершин с учётом видимости, получаем перспективу куба.

Перспективные изображения пространственных геометрических объектов могут располагаться на картинной плоскости Π_K ниже или выше линии горизонта hh, а также пересекать hh. При построении перспективного изображения объекта выбор расположения линии горизонта зависит от положения его в пространстве, от необходимости показать или скрыть его верхнюю часть, а также от задуманной композиции рисунка.

Сущность построения перспективы пространственного объекта, произвольно расположенного в предметном пространстве, фактически не отличается от только что рассмотренного. Однако, если неизвестны точки схода перспектив каких-либо сторон объекта, то необходимо выполнить дополнительные построения, связанные с нахождением перспективы линейного угла.

Н а рис. 1.39,а изображён линейный угол α со сторонами a и b, лежащими на предметной плоскости T. Перспективу α_K угла α можно построить по начальным точкам A_H, B_H и точкам схода F₁ и F₂ перспектив a_K и b_K прямых a и b. Точки схода F₁ и F₂ можно найти, если из точки зрения S провести лучи, параллельно a и b до пересечения с линией горизонта hh. Очевидно, что угол F₁ SF₂= α, a_K и b_K есть перспективы прямых, проведённых вдоль a и b, а α_K – перспектива заданного угла α.

Совместим плоскость горизонта H с картинной плоскостью Π_K поворотом по часовой стрелке вокруг линии hh (рис. 1.39,б). Тогда точка зрения S расположится выше линии hh на одной вертикали к главной точке P картины. При этом стороны угла α при вершине S опираются на точки схода F₁ и F₂. Так как SP – главное расстояние от точки зрения до картинной плоскости, то, если необходимо найти дистанционную точку D, проводим дугу окружности из точки P радиусом SP до пересечения с линией горизонта hh.

Определение натуральной величины отрезка прямой по его перспективе осуществляют при помощи масштабных точек, расположенных на линии горизонта hh.

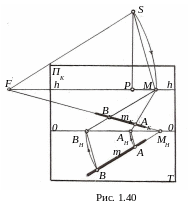Для нахождения масштабной точки M перспективы прямой m, расположенной в совмещённой с картинной Π_K предметной плоскости T, необходимо прежде всего задать положение точки зрения S и построить перспективу m_K прямой (рис. 1.40). Из точки S проводим прямую параллельно m до пересечения с линией горизонта hh в точке схода F. Соединяя начальную точку M_H с точкой схода F прямой, находим перспективу m_K прямой m. Из точки F радиусом FS описываем дугу окружности и на линии горизонта находим масштабную точку M. Точки S и M соединяем прямой. В результате получаем равнобедренный треугольник FSM, у которого стороны FS и FM равны.

Если необходимо измерить натуральную величину отрезка A_KB_K перспективы M_HF, то точки A_K и B_K соединяем прямыми с точкой M и на основании OO картины отмечаем точки A_H и B_H. Отрезок A_HB_H есть натуральная величина отрезка перспективы A_KB_K.

Действительно, если на прямую m дугами окружностей перенесём отрезки M_HA_H и A_HB_H, соединим хордами точки A и B с точками A_H и B_H, то образовавшиеся равнобедренные треугольники M_HAA_H и M_HBB_H подобны треугольникуFSM, как с соответственно параллельными сторонами. Стороны AA_H и BB_H треугольников параллельны между собой и стороне SM треугольника FSM. Поэтому прямые A_HM и B_HM являются перспективами параллельных прямых, проведённых вдоль сторон AA_H и BB_H, с точкой сходаM.

Перспективами треугольников M_HAA_H и M_HBB_H являются треугольники M_HA_KA_H и M_HB_KB_H. Следовательно, натуральной величиной отрезка A_KB_K перспективы является отрезок A_HB_H.

В случае если необходимо определить величину отрезка прямой общего положения по его перспективе, то все построения выполняем аналогично рассмотренным, но для перспективы вторичной проекции этой прямой. Через концы отрезка перспективы самой прямой и ту же масштабную точку проводим две прямые линии, на которую по линиям проекционной связи переносим полученную натуральную величину отрезка перспективы вторичной проекции. Расстояние между полученными точками является натуральной величиной отрезка перспективы прямой общего положения.

Пусть требуется построить перспективу прямого параллелепипеда, длина, ширина и высота которого соответственно равны l, m и n. Считать, что параллелепипед расположен на предметной плоскости и стороной основания, равной длине l, под произвольным углом наклонён к картинной плоскости Π_K. Перспективное изображение параллелепипеда на картинной плоскости должно быть расположено ниже линии горизонта.

Вначале на плоскости Π_K (рис. 1.41) зададим перспективу L_HF₁ прямой произвольного направления, проведённой вдоль ребра основания с длиной, равной l, где L_H и F₁ – соответственно начальная точка прямой и точка схода её перспективы. Зададим также перспективу A_K вершины нижнего основания параллелепипеда на линии L_HF₁.

Относительно совмещённой точки зрения S построим угол 90° и на

л инии горизонта hh отметим точку схода F₂ перспектив прямых, проведённых вдоль рёбер с длиной, равной ширине m параллелепипеда. Соединяем точки A_K и F₂.

От точки A_K отложим отрезок A_KB_K перспективы ребра параллелепипеда длиной l. Для этого из точки F₁ проводим дугу окружности радиуса F₁ S и находим масштабную точку M₁ на линии горизонта. Соединяем точки M₁ и A_K прямой и определяем точку A_H, от которой вправо на основании OO картины откладываем отрезок A_HB_H=l. Точки B_H и M₁ соединяем прямой и на её пересечении с перспективой L_HF₁ находим точкуB_K. Таким образом A_KB_K, есть перспектива стороны основания AB параллелепипеда, длина которого равна l.

Чтобы построить перспективу A_KE_K другой стороны основания, воспользуемся масштабной точкой M₂. Точки M₂ и A_K соединяем прямой, определяя тем самым точку M_H, и влево от неё откладываем отрезок M_HE_H, равный m. Точку E_H соединяем прямой с точкой M₂ и находим точкуE_K. Очевидно, что A_KE_K является перспективой стороны основания AE параллелепипеда, длина которой равна m.

Перспективы двух сторон основания позволяют построить перспективу всего основания. Используя точки схода F₁ и F₂ перспектив параллельных сторон основания, из точек B_K и E_K в точки F₂ и F₁ проводим прямые и находим точку C_K их пересечения. Итак, A_KB_KC_KE_K есть перспектива нижнего основания параллелепипеда.

Далее из вершин нижнего основания вверх проводим вертикальные прямые, по масштабу высот определяем перспективу одного из боковых рёбер с длиной, равной n. Как видно из рис. 1.41, остальные вершины верхнего основания построены с использованием точек схода F₁ и F₂ перспектив параллельных сторон параллелепипеда.

Отметим, что каждая прямая, расположенная в предметной плоскости T имеет свою масштабную точку.

Способ перспективных масштабов и использование масштабных точек позволяют строить перспективные изображения самых разных пространственных объектов с известными размерами.

4. Способ применения дистанционной точки. Известно, что пучок параллельных между собой и предметной плоскости T прямых, наклонённых к картинной плоскости Π_K под некоторым произвольным углом, имеют общую точку схода их перспектив, расположенную на линии горизонта hh. Если же эти прямые наклонены к картинной плоскости под углом 45°, то точка схода их перспектив совпадает с дистанционной точкой D.

Известно также, что пучок параллельных между собой прямых и перпендикулярных к картинной плоскости имеют точку схода их перспектив в главной точке P картины.

Если известны начальные точки прямых обеих групп, то, выбрав расположение главной P и дистанционной D точек на картинной плоскости, можно построить перспективы таких прямых, лежащих выше предметной плоскости. Очевидно, перспективу пространственного геометрического объекта в этом случае можно построить по его характерным точкам, путём проведения через каждую двух вспомогательных прямых, одну из которых под углом 45°, а другую перпендикулярно к картинной плоскости.

Р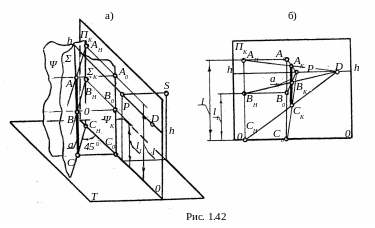 ассмотрим методику нахождения начальных точек указанных прямых, попарно проведённых через точки A, B и C (рис. 1.42, а) вертикально расположенного стержня a. Точки A и B стержня расположены выше и ниже плоскости горизонта соответственно на расстоянии l и l₁ от плоскости T, а точка C лежит на ней. Прямые, проведённые через рассматриваемые точки под углом 45° к Π_K, образуют плоскость Σ с картинным следом Σ_K, на котором находятся начальные точки A_H, B_H и C_H.

Аналогично прямые, проведённые через эти же точки перпендикулярно к Π_K, образуют плоскость Ψ с картинным следом Ψ_K и начальными точками A₀, B₀ и C₀ на нём. Как видно из приведённых построений, картинные следы Σ_K и Ψ_K перпендикулярны основанию OO картины, а начальные точки A_H, A₀ и B_H, B₀ находятся на тех же расстояниях l и l₁ от плоскости T, что и точки A и B.

На рис. 1.42, б показана фронтально расположенная картинная плоскость Π_K с выполненными построениями перспектив A_K, B_K, C_K точек A, B, C и перспективы a_K стержня a. Для этого через начальные точки и дистанционную точку D были проведены перспективы соответствующих пар прямых, в точках пересечения которых были найдены перспективы заданных точек и затем построена перспектива стержня.

П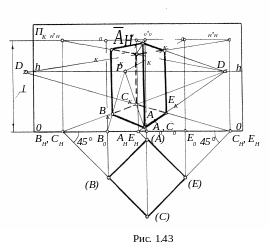 усть требуется построить перспективу прямого параллелепипеда с нижним основанием в виде квадрата ABCE, лежащего в предметной плоскости T, и верхним основанием в виде квадрата , отстоящего от плоскости T на расстоянии l (рис. 1.43). Так как все боковые рёбра перпендикулярны к плоскости T, то ортогональная проекция верхнего основания совпадает с нижним основанием ABCE. Отметим на картинной плоскости Π_K линию горизонта hh, главную точку P и основание OO картины. Поскольку главное расстояние SP известно, то на линии горизонта hh отметим дистанционные точки D₁ и D₂ перспектив параллельных сторон, наклонённых под углом 45° к Π_K, нижнего и верхнего оснований параллелепипеда.

Построение перспективы параллелепипеда начинаем с построения перспективы A_KB_KC_KE_K нижнего основания, последовательно определяя перспективы A_K, B_K, C_K, E_K точек A, B, C, E нижнего основания. Для этого

через каждую точку нижнего основания проводим по две прямых линии, одна из которых идёт под углом 45°, а другая перпендикулярно основанию OO картины. Соединяя точки A_H, B_H, C_H и E_H пересечения с Π_K прямых, проведённых под углом 45° к линии OO , с точкой D₁ и точки A₀, B₀, C₀ и E₀ пересечения с Π_K прямых, перпендикулярных к линии OO, с точкой P, найдём перспективы A_K, B_K, C_K и E_K точек нижнего основания.

Прямые линии через выбранные точки под углом 45° к линии OO можно проводить с наклоном от точки и в другую сторону. Точность построения перспектив точек, как например для точек C и E, где и – точки пересечения таких прямых с линией OO, не изменяется. В этом случае используется точка D₂ для параллельных прямых линий, но наклоненных к линии OO под углом 45° в другую сторону.

Точки , , и верхнего основания параллелепипеда находятся на расстоянии l от предметной плоскости T, а следовательно от основания OO картины. Поэтому прямые линии, проведённые параллельно плоскости T, пересекут картинную плоскость Π_K на расстоянии l от линии OO в точках _H, _H, _H и _H. Так как боковые рёбра параллелепипеда перпендикулярны к плоскости T, то точки A_H и _H, B_H и _H, C_H и _H, _H и всегда находятся на прямых, перпендикулярных линии горизонта hh.

Прямые линии, проведённые перпендикулярно картинной плоскости Π_K через точки , , и верхнего основания параллелепипеда, также пересекут картинную плоскость Π_K на расстоянии l от линии OO в точках ₀, ₀, ₀ и ₀. Соединив найденные точки _H, _H, _H и _H с точкой D₁, а точки ₀, ₀, ₀ и ₀ с точкой P, в точках пересечения соответствующих пар перспектив прямых, находим перспективы _K, _K, _K и _K точек , , и верхнего основания. Соединяя последовательно найденные перспективы точек нижнего и верхнего основания прямыми линиями с учётом их видимости, получаем перспективу параллелепипеда.

При построении перспективы вертикально расположенного цилиндра с целью упрощения построений рекомендуется вписать его в параллелепипед, чтобы использовать точки схода перспектив, совпадающих с дистанционными точками параллельных сторон его оснований. Далее построения выполняются аналогично изложенному выше. После построения перспективы параллелепипеда необходимо дополнительно выбрать не менее четырёх дополнительных точек на окружностях верхнего и нижнего оснований, построить их перспективы, перспективы этих окружностей и самого цилиндра.

5. Способ малой и большой картины. При построении перспективы объекта следует стремиться не выходить за рамки картинной плоскости Π_K. В этом случае применяют способ малой картины, который заключается в том, что перспективу объекта сначала строят на малой картине, а затем переносят на большую основную картину.

На рис. 1.44, а представлен процесс проецирования на большую Π_K и малую Π_K1 картинные плоскости, параллельных между собой и перпендикулярных к лучу зрения SP. Прямоугольник 1234 рамки большой картины Π_K подобен прямоугольнику 1₁2₁3₁4₁ рамки малой картины Π_K1. Коэффициент подобия равен отношению расстояний точки зрения S от плоскостей Π_K и Π_K1. На рис. 1.44, б плоскости Π_K и Π_K1 совмещены и изображены фронтально.

П ри переходе от малой картины к большой требуется выполнять свойства подобных геометрических фигур. Прежде всего точки подобных фигур расположены на одной прямой, проходящей через центр подобия. В

данном случае центром подобия является главная точка P картины. Кроме того отрезок перспективы малой картины должен быть параллелен этому же отрезку перспективы, построенному на большой картине.

Д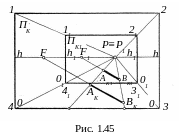 ля пояснения способа малой и большой картины ограничимся рассмотрением построения отрезка A_KB_K перспективы некоторого отрезка прямой, лежащего в предметной плоскости и заданного на малой картине Π_K1 в виде перспективы A_K1B_K1 (рис. 1.45), с увеличением в два раза.

Так как подобные точки обеих картин расположены на одной прямой, проходящей через центр подобия P, то сначала находим вершины 1, 2, 3 и 4 прямоугольника рамки большой картины. Для этого из точки P в точки 1₁, 2₁, 3₁ и 4₁ проведём лучи и отложим на одном из них, например на луче, проходящем через точку 1₁, отрезок P1₁ два раза. Получим вершину 1 рамки. Поскольку стороны рамок картины соответственно параллельны, то, опираясь на точку 1, построим стороны прямоугольника большой картины с вершинами 1, 2, 3 и 4.

В нашем случае увеличение картины выполнено в два раза. В связи с этим увеличением все элементы картины должны быть взяты в отношении, соответствующему коэффициенту подобия фигур. Для принятого увеличения в два раза необходимо принять PF=2PF₁, PA_K=2P₁A_K1 и т. д. В результате на картинной плоскости Π_K получим перспективу A_KB_K отрезка, увеличенную в два раза.

Перспективное изображение объекта на большой картине можно увеличить в несколько раз. Естественно, можно выполнить и обратную задачу, когда осуществляют переход от изображения на большой картине к изображению на малой картине.

6. Способ перспективной сетки. С помощью перспективной сетки можно построить перспективные изображения объектов сложной геометрической конфигурации не только плоской формы (план участка земли и помещения, кружева и орнаменты, перфорации и т.д.), но и пространственных (предметы ландшафта и интерьера).

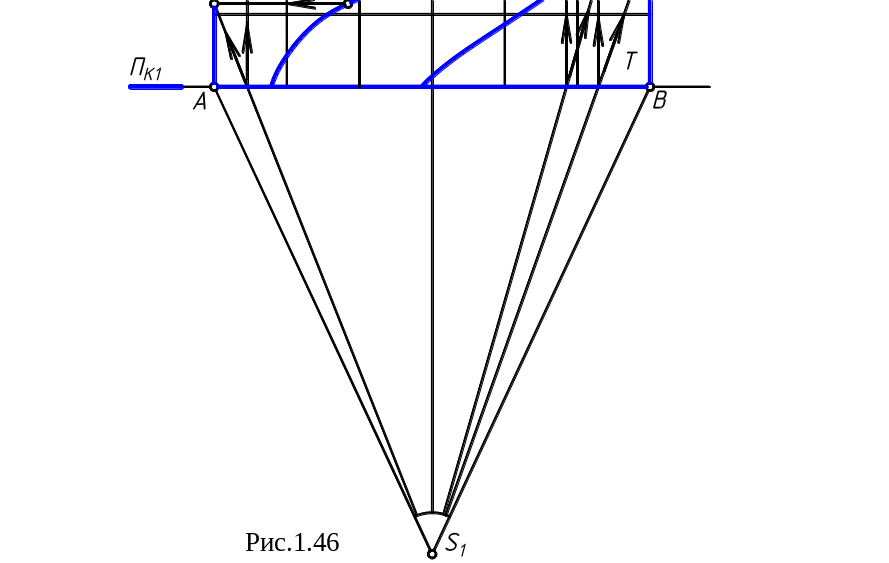
Сущность способа состоит в следующем. На предметной плоскости вычерчивают план (участка земли или помещения, орнамента или перфорации, предметов ландшафта или мебели и т.д.). На рис.1.46 в качестве примера на предметной плоскости Т выполнено разбиение фрагмента АВСЕ плана участка земли на квадраты, и на картинной плоскости П_К построены перспективы этих квадратов, образующие горизонтальную перспективную сетку.

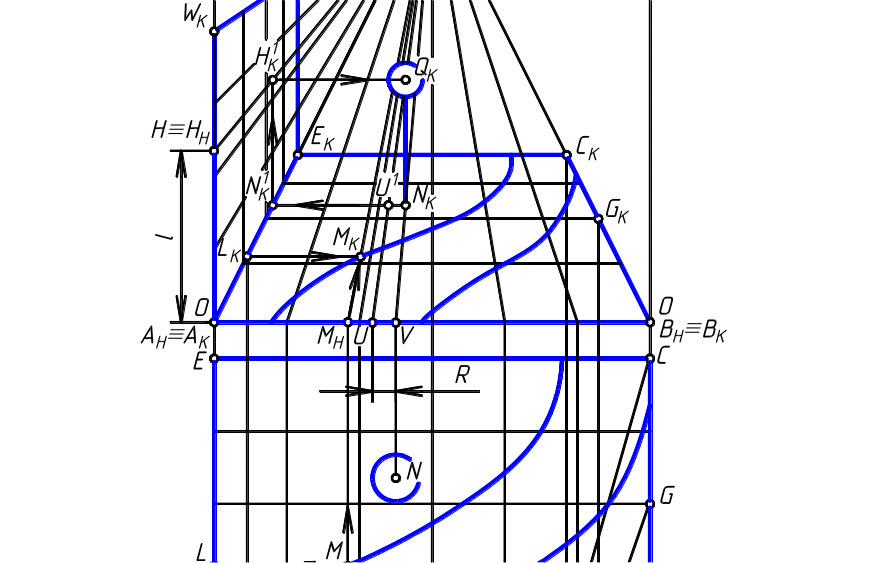
Для этого сначала задаём линейный масштаб и по нему строим план фрагмента участка земли в виде дорожки и осветительного столба с плафоном в виде сферы.

Далее на плане задаём точку зрения S так, чтобы она отстояла от картинной плоскости П_К не менее, чем на 1,5…2,0 ширины картины. В данном случае угол зрения φ = 52º, что незначительно повлияет на перспективные искажения. Поэтому главное расстояние SР взято чуть более ширины картины. Для большей наглядности выбираем высокий горизонт и, опуская из точки зрения S перпендикуляр к линии горизонта hh, находим главную точку Р.

В рассматриваемом случае фрагмент плана участка разбит по ширнине на 6, а в глубину на 4 равные части. Вертикальные разделительные линии квадратов плана расположены в плоскости Т и перпендикулярны П_К. Поэтому перспективы этих прямых идут от начальных точек пересечения их с основанием ОО к главной точке Р картинной плоскости П_К. Начальными точками прямых АЕ и ВС плана участка будут А_Н ≡ А_К и В_Н ≡ В_К , а перспективами этих прямых – соответственно А_НР и В_Н Р.

Для построения контура перспективной сетки достаточно из точки зрения S направить лучи зрения в ближайшие и дальние вершины углов плана участка, т.е. в точки А, В и С, Е, и найти перспективы вершин углов и сторон контура. Так, например, чтобы найти перспективу С_К вершины угла С плана, необходимо провести луч зрения SC, отметить точку пересечения его с П_К , из которой поднять вертикально вверх прямую проекционной связи до пересечения с перспективой прямой В_НР в точке С_К.

Завершая построение перспективной сетки плана участка, проводим горизонтальные разделительные линии. Тогда, например, для построения перспективы горизонтальной прямой плана, проходящей черех точку G, нужно найти перспективу G_К этой точки. С этой целью проводим луч зрения SG , отмечаем точку пересечения его с П_К , из которой проводим линию проекционной связи вертикально вверх и на пересечении её с перспективой В_НС_К находим перспективу точки G_К . Затем из этой точки проводим горизонтальную прямую параллельно основанию ОО. Такие горизонтальные прямые проводим через все точки деления контура плана участка в глубину, получая в результате перспективную сетку.

Перспективное изображение дорожки строим по характерным точкам её контура. Так, перспективу М_К произвольно взятой точки М контура найдём, если через точку М на плане участка проведём горизонтальную прямую до пересечения в точке L со стороной АЕ. Тогда, выполнив построения как и для точки G, найдём перспективу L_К.

Очевидно, перспектива М_К будет расположена в точке пересечения перспектив L_КМ_К и М_НР соответственно горизонтальной прямой LМ и перпендикулярной к основанию ОО прямой М_НМ с начальной точкой М_Н..

Точно также находим перспективы всех характерных точек контура дорожки, которые последовательно соединяем плавной кривой линией, а также перспективу N_К основания осветительного столба.

Для построения перспективы плафона необходимо знать высоту l осветительного столба и радиус R сферы плафона. Дополним построенную горизонтально расположенную перспективную сетку вертикальной перспективной сеткой, расположенной в вертикальной плоскости, перпендикулярной к П_К . Эта плоскость в виде прямоугольника на рис.1.46 задана перспективой А_КЕ_КК_КW_К , в которой построена перспективная сетка из таких же квадратов, как и на плане участка, т.е. в принятом ранее линейном масштабе. При этом перспективы вертикальных линий квадратов проведены через точки деления стороны А_КЕ_К горизонтальными разделительными линиями, а линии квадратов, параллельные предметной плоскости Т – через точки, расположенные на стороне А_КW_К на одинаковых расстояниях, равных стороне квадрата на плане.

По масштабу высот на стороне А_КW_К вертикальной перспективной сетки откладываем высоту l осветительного столба от его основания до центра сферы плафона и из отмеченной точки Н ≡ Н_Н в главную точку Р проводим перспективу прямой, перпендикулярной к П_К, где Н_Н – начальная точка этой прямой. Затем из точки N_К проводим горизонтальную прямую до пересечения с перспективой А_КЕ_К в точке N . Из точки N проводим вертикально вверх прямую до пересечения с перспективой Н_НР в точке Н . Из приведённых построений видно, что отрезок N Н равен высоте перспективы осветительного столба. Далее из точек N_К и Н проводим соответственно вертикальную и горизонтальную линии до пересечения в точке Q_К, которая будет являться перспективой центра сферы.

Перспектива очерка сферы построена с помощью масштаба широт. Радиус окружности очерка сферы в перспективе определяем следующим образом. Из точки N плана участка проводим перпендикуляр NV к основанию ОО картинной плоскости П_К . От точки V на линии ОО откладываем отрезок, равный известной величине радиуса R сферы плафона, и соединяем отмеченную точку U с точкой Р прямой, на пересечении которой с прямой N_К N отмечаем точку U¹. Далее радиусом, равным величине отрезка N_КU¹, проводим из центра Q_К окружность, которая является перспективой очерка сферы плафона.