3. Построение перспектив прямых при недоступной точке схода.

При построении перспектив геометрических объектов часто необходимо строить параллельные друг другу прямые, точка схода перспектив которых может находиться далеко за пределами картинной плоскости Π_K. Существуют различные способы выполнения построений перспектив параллельных прямых с недоступной точкой схода. Рассмотрим лишь некоторые способы.

3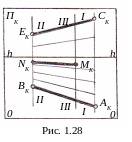 .1. Способ построения перспектив параллельных прямых. Пусть на картинной плоскости Π_K (рис. 1.28) изображены перспективы A_KB_K и C_KE_K параллельных прямых с недоступной точкой схода, лежащей на лини горизонта hh. Требуется построить ещё некоторое количество перспектив прямых с той же точкой схода. Для этого через точки A_K и B_K проводим вертикали I-I и II-II и от точек пересечения их с линией горизонта hh вверх и вниз делим на равное количество одинаковых частей и соединяем тонкими линиями соответствующие точки деления. На рис. 1.28 эти вертикали разделены вверх от линии горизонта hh на 2 части, а вниз на 4 части. В результате получили так называемую перспективную сетку, состоящую из определенного количества перспектив, параллельных между собой прямых.

Если через некоторую точку M_K, являющейся перспективой точки M, требуется построить перспективу M_KN_K, прямой MN с той же точкой схода, то нужно выполнить следующие построения. Через точку M_K провести вертикаль III-III, тем самым разбив её на участки от линии горизонта hh до перспективы A_KB_K на две части. Участок вертикали II-II от линии горизонта hh до точки B_K точкой N_K также необходимо разбить на две пропорциональные рассмотренные части. Отрезок M_KN_K есть перспектива прямой MN.

3.2. Применение дробных дистанционных точек. От главной точки P картины дистанционная точка D находится на том же расстоянии что и точка зрения S от точки P. Расстояние между точками S и P следует принимать не менее двукратной высоты картины. Поэтому при построении перспективных изображений объектов дистанционная точка D, лежащая на линии горизонта hh, часто находится за пределами картины. В этом случае целесообразно применять дробную дистанционную точку D/2, D/3, D/4 и т. д.

На рис. 1.29, а на картинной плоскости Π_K задана перспектива A_KB_K

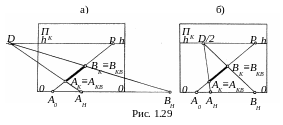
отрезка прямой, расположенной в предметной плоскости T и перпендикулярной к основанию ОО картины. Дистанционная точка D расположена на линии горизонта hh вне границ картинной плоскости Π_K. Для определения длины отрезка AB по его перспективе A_KB_K воспользуемся масштабом глубин.

Как было рассмотрено выше, точки A₀, A_H и B_H и являются начальными точками прямых соответственно перпендикулярной к основанию ОО и двух других, проведенных через точки A и B под углом 45° к основанию ОО. Поскольку треугольник A₀B_KB_H в натуре равнобедренный и прямоугольный с прямым углом при вершине A₀, то отрезок A₀B_K равен отрезку A₀B_H. Аналогично отрезок A₀A_K равен отрезку A₀A_H. Поэтому длина отрезка равна отрезку A_HB_H.

Рассмотрим теперь задачу определения длины того же отрезка AB с использованием дробной дистанционной точки D/2 (рис. 1.29, б). Выполнив аналогичные построения, как и для дистанционной точки D, убеждаемся, что длина отрезка AB равна удвоенной длине отрезка A_HB_H. Таким образом, при уменьшении отстояния дистанционной точки D от главной точки P картины в несколько раз измеренная длина отрезка AB на основании картины ОО должна быть увеличена во столько же раз.

4. Перспектива плоских геометрических фигур, лежащих в предметной плоскости. Рассмотрим построение перспектив простейших геометрических фигур.

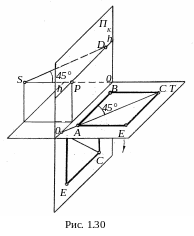
4.1. Перспектива квадрата. Пусть в предметной плоскости T расположен квадрат ABCE, у которого сторона AB параллельна основанию ОО картины (рис. 1.30). Диагональ квадрата к основанию ОО картины наклонена под углом 45°, поэтому луч SD зрения, будучи параллельным AC, так же наклонён к SP (главное расстояние) под углом 45°. Тогда треугольник SPD равнобедренный и точка схода перспективы диагонали AC находится в дистанционной точке D на линии горизонта hh.

Отметим также, что сторона AE квадрата перпендикулярна к плоскости картины П_К и имеет точку схода перспективы AE в точке P.

С овместим предметную плоскость T поворотом вокруг основания ОО по часовой стрелке с плоскостью картины. После совмещения плоскостей (рис. 1.31) продолжим диагональ AC и стороны AE и BC квадрата до пересечения их с основанием ОО. По известным точкам схода D и P и точкам пересечения этих прямых с плоскостью П_К строим их перспективы, в точках пересечения которых находятся перспективы A_K и C_K точек A и C квадрата. Поскольку стороны AB и EC квадрата параллельны основанию ОО картины, то их перспективы A_KB_K и C_KE_K параллельны линии горизонта hh. Таким образом, фигура A_KB_KC_KE_K является перспективой квадрата ABCE.

4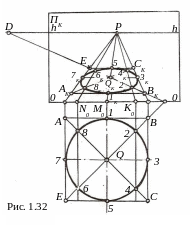 .2. Перспектива окружности. Рассмотренный приём построения перспективы квадрата применим при построении перспективы окружности, лежащей в предметной плоскости. Для облегчения выполняемых построений вокруг окружности описываем квадрат ABCE, как показано на рис. 1.32 и строим его перспективу A_KB_KC_KE_K.

Перспективу окружности строим по восьми точкам, точки 1, 3, 5 и 7 которой расположены на серединах сторон квадрата, а точки 2, 4, 6, и 8 на пересечении его диагоналей с окружностью. Если начальные точки M₀, N₀ и K₀ прямых, проведенных через точки 6 и 8, 5 и 1 и 4 и 2 перпендикулярно к основанию OO картины, соединить с главной точкой картины, то на пересечении полученных перспектив этих прямых с перспективами сторон и диагоналей квадрата получим перспективы точек 1_K, 2 _K, 4 _K, 5_K, 6_K, 8_K и Q_K центра Q окружности. Перспектива 3_K7_K отрезка 3-7, параллельного предметной плоскости П_К, будет параллельна основанию OO картины.

Соединив по лекалу найденные перспективы восьми точек окружности, в результате получим эллипс. При построении перспективы больших по размеру окружностей необходимо задавать большее количество точек. Чтобы избежать серьёзных перспективных искажений, главную точку P картины следует располагать в пределах не более диаметра окружности.

Используя указанный приём, можно построить перспективу плоской геометрической фигуры, лежащей в предметной плоскости T, любой конфигурации. Для этого достаточно выбрать характерные точки на плоской геометрической фигуре, проведя через каждую из них по две вспомогательные прямые под углом 45° и перпендикулярно к основанию OO картины. По известным точкам схода D и P перспектив этих прямых находим перспективы искомых точек и построим по ним перспективу геометрической фигуры.

5. Деление отрезка в заданном отношении. Из геометрии известно, что для того, чтобы разделить отрезок AB прямой (рис. 1.33, а) в заданном отношении, например AC:BC=1:2, необходимо выполнить следующие действия. Через точку A под произвольным углом φ проводим прямую линию и откладываем на ней три равных отрезка. Через точки B₁ и B проводим прямую. Параллельно ей из точки C₁ проводим другую прямую, которая точкой C разделит отрезок AB в отношении 1: 2.

На рис. 1.33, б задана перспектива A_HB_K отрезка AB прямой, расположенной в предметной плоскости T с начальной точкой A_H. Требуется найти перспективу C_K точки C, которая разделит его в отношении 1: 2.

Используя масштаб широт, на основании OO картины от точки A_H откладываем произвольной длины отрезок A_HC_H и отрезок C_HB_H=2A_HC_H. Через начальные точки B_H и C_H проводим перспективы двух параллельных прямых. Точка схода F перспектив прямых находится на линии горизонта hh. Поэтому вначале находим точку схода F на продолжении прямой B_HB_K в точке пересечения с линией hh, а затем соединяем точки C_H и F, определяя положение точки C_K. Так как отрезки B_KC_K и B_HC_H равны, то точка C_K делит перспективу A_HB_K в отношении 1: 2.

На рис. 1.33, в перспектива A_KB_K отрезка AB прямой, расположенной в предметной плоскости T и не пересекающей основание OO картины, не имеет начальной точки A_H. В этом случае через произвольно выбранную точку схода F и перспективы A_K и B_K проводим перспективы параллельных прямых до пересечения с основанием OO в точках A_H и B_H.

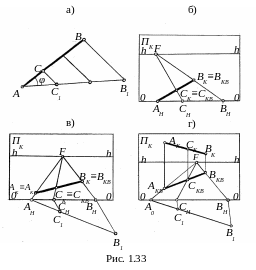
Для деления перспективы A_KB_K точкой C_K в том же отношении 1: 2 от точки A_H под произвольным углом к OO проводим прямую и откладываем три равных отрезка, отмечая точки B₁ и C₁ так, чтобы B₁C₁=2 A_HC₁. Соединяем точки B₁ и B_H, а из точки C₁ проводим прямую параллельно отрезку B₁B_H, получая на линии OO точку C_H, соединяем точку C_H с точкой F и находим точку C_K, которая делит перспективу A_KB_K в отношении 1: 2.

В случае, если отрезок AB прямой не лежит в предметной плоскости T, то деление его перспективы A_KB_K точкой C_K в заданном отношении 1: 2 нужно проводить по перспективе A_KBB_KB вторичной проекции отрезка (рис. 1.33, г). Определяя рассмотренным выше способом точку C_KB, по линии проекционной связи находим искомую перспективу C_K.

Рассмотренный приём членения отрезка перспективы на отдельные элементы с успехом можно использовать при построении интерьера какого-либо помещения. Пусть на картинной плоскости П_К задана или построена перспектива A_KB_KC_KЕ_K боковой стены помещения с дверным и оконным проёмами (рис. 1.34). Расстояние между вертикалями и горизонталями этих проёмов известны. Тогда, используя перспективные масштабы широт и высот, от точки A_K, которая одновременно является начальной точкой A_H перспективы A_KB_K отрезка AB, на основании OO картины откладываем отрезки A_K1_H, 1_H2_H,…, 4_HB_H, равные интервалам между вертикалями проёмов. На отрезке A_KЕ_K, который является картинным следом плоскости стены, от точки A_K откладываем отрезки A_K5_H и A_K6_H, равные интервалам между горизонталями проёмов.

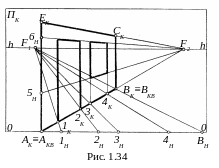
Перспектива A_KB_K будет разделена на пропорциональные отрезки A_K1_K, 1_K2_K,…, 4_KB_K , если соединить прямой точки B_H и B_K и найти точку схода F₁ перспективы этой прямой и точки 1_H, 2_H,…, 4_H соединить с точкой F₁, получая в результате пучок параллельных прямых.

Соединяя точки 5_H и 6_H с точкой F₂ прямыми, получаем перспективы параллельных между собой горизонталей, которые позволяют определить горизонтальные участки дверного и оконного проёмов.