1.4. Перспектива плоскости

Известно, что плоскость можно задавать: с помощью трёх точек, не лежащих на одной прямой; прямой и точкой, не лежащей на ней; двумя параллельными прямыми; двумя пересекающимися прямыми. В практике построения перспективных изображений плоскость обычно задают в виде плоской фигуры, ограниченной отрезками прямых, и следами.

Следом плоскости называется линия пересечения её с картинной Π_K или с предметной T плоскостью проекций. При этом линия пересечения заданной плоскости с картинной плоскостью называется картинным следом, а с предметной плоскостью – предметным следом.

Плоскости разделяют на плоскости общего положения и частного положения.

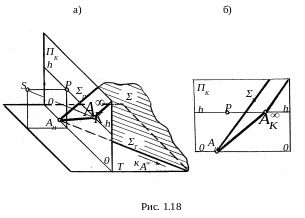
1. Плоскости общего положения. Плоскость общего положения не параллельна и не перпендикулярна картинной πk и предметной t плоскостям проекций.

На рис. 1.18, а плоскость Σ общего положения задана картинным следом Σ_П и предметным следом Σ_T. При построении перспективы плоскости Σ имеем ввиду, что картинный след Σ_П одновременно является его перспективой.

Для построения перспективы предметного следа Σ_Т найдём начальную точку A_H пересечения его с плоскостью Π_K и перспективу

бесконечно удалённой точки A^∞. Точка A_H находится в точке пересечения следов Σ_П и Σ_T на основании ОО картины. Перспектива точки A^∞ находится на пересечении луча, проведённого из точки зрения S в точку A^∞ параллельно следу Σ_T, с линией горизонта hh. Соединяя прямой полученные точки A_H и , получаем перспективу предметного следа Σ_T.

Если из точки зрения S проведём пучок лучей в бесконечно удалённые точки плоскости Σ, то лучи, будучи параллельными этой плоскости, образуют некоторую плоскость, которая пересечёт картинную плоскость Π_K от точки по прямой, параллельной Σ_П. По существу построенная прямая является перспективой бесконечно удалённой прямой заданной плоскости Σ.

Выполненные построения перспективы плоскости Σ общего положения показаны на рис. 1.18, б на картинной плоскости Π_K, расположенной фронтально.

2 Рис. 1.19 . Плоскости частного положения. Плоскости частного положения перпендикулярны или параллельны предметной или картинной плоскостям.

На рис. 1.19, а плоскость Σ перпендикулярна предметной плоскости Т и задана предметным Σ_T и картинным Σ_П следами. Картинный след Σ_П одновременно является его перспективой. Начальной точкой следа Σ_T является точка A_H пересечения его с основанием ОО картины. Если из точки зрения S проведём луч параллельно следу Σ_T, то на пересечении его с линией горизонта hh найдём перспективу бесконечно удалённой точки A^∞. Тогда прямая A_H является перспективой предметного следа Σ_T.

Пучок лучей, проведённых из точки зрения S в бесконечно удалённые точки заданной плоскости Σ, образуют плоскость, которая будет параллельна ей и пересечёт картинную плоскость Π_K от точки по прямой, параллельной Σ_П. Эта прямая является перспективой бесконечно удалённой прямой плоскости Σ.

На картинной плоскости Π_K (рис. 1.19, б) показана построенная перспектива плоскости Σ, перпендикулярной к предметной плоскости T.

Если плоскость Σ перпендикулярна картинной плоскости Π_K (рис.1.20 а, б) и задана картинным Σ_П и предметным Σ_T следами, то, в отличие от рассмотренного выше примера, точка схода следа Σ_T, перпендикулярного к Π_K, будет находиться в главной точке P картины.

Плоскость, параллельная предметной плоскости T, имеет картинный след, параллельный основанию OO картины. Перспектива такой плоскости изображается в виде картинного следа этой плоскости и линии горизонта hh, которая является перспективой бесконечно удаленной прямой плоскости.

Если же плоскость параллельна картинной плоскости Π_K и имеет предметный след, параллельный основанию OO картины, то перспектива её будет изображена в виде прямой также параллельной основанию OO.

Все точки, расположенные выше перспективы предметного следа этой плоскости, будут ей принадлежать.