1.3. Взаимное расположение прямых линий

Прямые в пространстве могут быть параллельными между собой, пересекаться и скрещиваться.

1. Параллельные прямые. Как было показано выше прямые общего положения, а также параллельные предметной и перпендикулярные картинной плоскостям (в том числе расположенные в предметной плоскости) имеют точки схода их перспектив. Более того, если две (или более) прямые каждой разновидности в пространстве параллельны, то их перспективы проходят через общую точку схода.

В зависимости от направления прямых точки схода их перспектив могут занимать разные положения на картинной плоскости.

Рис. 1.13

Так, например, параллельные между собой прямые a, b и c общего положения (рис. 1.13, а) имеют начальные точки A_H, B_H и C_H и точку схода F₁ их перспектив, расположенную выше линии горизонта hh на пересечении луча зрения, проведённого из точки S параллельно этим прямым, с картиной плоскостью Π_K. Перспективы прямых a, b и c будут изображены в виде отрезков a_K, b_K и c_K прямых от точки F₁ схода до начальных точек A_H, B_H и C_H пересечения прямых с картинной плоскостью Π_K.

На рис. 1.13, б картинная плоскость Π_K изображена фронтально и на ней показаны выполненные построения перспектив a_K, b_K и c_K заданных прямых. Прямые a, b и c называются восходящими. Точка схода F₁ перспектив восходящих прямых всегда располагается выше линии горизонта и называется воздушной точкой схода.

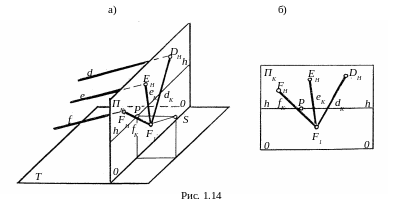Перспективы параллельных прямых d, e и f на рис. 1.14, а изображены в виде отрезков d_K, e_K и f_K от точки схода F₁ до начальных точек D_H, E_H и F_H пересечения заданных прямых с картинной плоскостью Π_K. На фронтально расположенной плоскости Π_K (рис. 1.14, б) показаны выполненные построения перспектив d_K, e_K и f_K заданных прямых. Прямые d, e и f называются нисходящими. Точка F₁ схода перспектив нисходящих прямых располагается ниже линии горизонта и называется земной точкой схода.

П усть в предметном пространстве находятся параллельные между собой и параллельные предметной плоскости Τ прямые a и b, а в плоскости Τ – параллельная им прямая c (рис. 1.15, а).

Точка F схода перспектив прямых a и b находится на линии горизонта hh, так как луч зрения, проведённый из точки S зрения параллельно этим прямым, расположен в плоскости горизонта. Перспектива прямой c также будет иметь точку схода F. Соединив отрезками прямых точку схода F с начальными точками A_H, B_H и C_H пересечения прямых a, b и c с плоскостью Π_K, получим перспективы a_K, b_K и c_K этих прямых. На рис. 1.15, б показаны выполненные построения перспектив a_K, b_K и c_K заданных прямых только на картинной плоскости Π_K.

Таким образом прямые, параллельные между собой и предметной плоскости, имеют общую точку схода их перспектив, расположенную на линии горизонта hh.

Как было показано ранее (см. раздел 1.2) прямые линии, перпендикулярные картинной плоскости, имеют точку схода их перспектив, совпадающую с центром P картинной плоскости Π_K (рис. 1.12). По существу на этом рисунке имеем две прямые a и b и две вторичные проекции a_T и b_T параллельные между собой и перпендикулярные плоскости Π_K. На картинной плоскости Π_K, расположенной фронтально (рис. 1.16), представлены перспективы a_K, b_K, a_KВ и b_KВ этих прямых в виде отрезков прямых от начальных точек A_H, B_H, A_О и B_О до точки схода в главной точке P картины.

И так, перспективы прямых, перпендикулярных картинной плоскости, имеют общую точку схода в главной точке P картины.

Отметим также, что параллельные между собой прямые, которые параллельны картинной плоскости Π_K, не имеют точек схода их перспектив. Перспективы таких прямых линий параллельны этим прямым в пространстве.

Параллельные между собой прямые, которые перпендикулярны предметной плоскости T, тоже не имеют точек схода их перспектив. Перспективы этих прямых всегда перпендикулярны основанию ОО картины.

Следует иметь в виду, что любой геометрический элемент в виде точки, прямой или кривой линии, а также плоской фигуры, расположенный в картинной плоскости Π_K, имеет перспективу, совпадающую с этим элементом.

2. Пересекающиеся и скрещивающиеся прямые. Если две прямые пересекаются, то точки пересечения их перспектив и перспектив вторичных проекций должны лежать на одной линии проекционной связи, перпендикулярной к линии горизонта hh.

На рис. 1.17, а показаны перспективы a_K и b_K двух пересекающихся прямых a и b общего положения и перспективы a_KВ и b_KВ вторичных проекций этих прямых на картинной плоскости Π_K. Здесь перспектива M_K точки пересечения M прямых a и b и перспектива M_KВ вторичной проекции точки пересечения лежат на одном перпендикуляре к линии горизонта hh. Другой вариант невозможен, так как точка пересечения M принадлежит и прямой a и прямой b.

На рис. 1.17, б показаны перспективы a_K и b_K двух скрещивающихся прямых a и b общего положения и перспективы a_KВ и b_KВ вторичных проекций этих прямых на картинной плоскости Π_K. Здесь точке пересечения перспектив a_K и b_K соответствуют точки M и N, первая из которых расположена на прямой a, вторая – на прямой b. Такой же вывод можно сделать о точке пересечения перспектив a_KВ и b_KВ вторичных проекций заданных прямых.